Sturges regel

Vi forklarer hva Sturges -regelen er, dens anvendelse og gir flere eksempler

Hva er Sturges -regelen?

De Sturges regel Det er et kriterium som brukes for å bestemme antall klasser eller intervaller som er nødvendige for å tegne et sett med statistiske data grafisk. Denne regelen ble uttalt i 1926 av den tyske matematikeren Herbert Sturges.

Sturges foreslo en enkel metode, basert på antall X -prøver som tillot å finne antall klasser og deres rekkeviddeområde. Sturges -regelen er mye brukt fremfor alt i statistikkområdet, spesielt for å bygge frekvenshistogrammer.

Forklaring

Sturges -regelen er en empirisk metode som er mye brukt i beskrivende statistikk for å bestemme antall klasser som må eksistere i et frekvenshistogram, for å klassifisere et sett med data som representerer en prøve eller en populasjon.

I utgangspunktet bestemmer denne regelen bredden på grafiske beholdere, frekvenshistogrammer.

For å etablere sin regel Herbert Sturges betraktet som et ideelt frekvensdiagram, som består av K -intervaller, der i -dette intervallet inneholder et visst antall prøver (i = 0, ... k - 1), representert som:

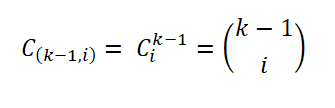
Dette antallet prøver er gitt av antall måter en delmengde av et sett kan trukket ut; Det vil si av binomialkoeffisienten, uttrykt som følger:

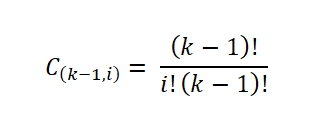Deretter er Sturges relatert til at frekvenshistogrammet vil tilnærme en normalfordeling når antall intervaller (k) øker i henhold til den sentrale teoremet til grensen. På en slik måte at antall prøver av hvert av intervallene kan beregnes:

Det kan tjene deg: enegon: egenskaper, hvordan lage en enegon, eksempler

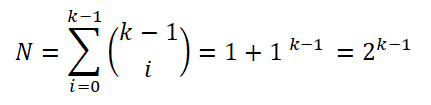
For å forenkle uttrykket anvendte han egenskapene til logaritmer i begge deler av ligningen:

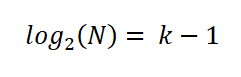
Sturges slo fast at det optimale antallet K -intervaller er gitt av uttrykket:

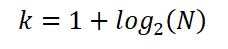
Det kan også uttrykkes som:

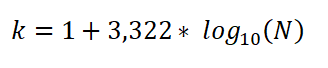
I dette uttrykket:

• K er antall klasser.
• N er det totale antall observasjoner i prøven.
• Log er den vanlige baselogaritmen 10.

For eksempel, for å utdype et frekvenshistogram som uttrykker en tilfeldig prøve av staturen til 142 barn, er antall intervaller eller klasser som distribusjonen vil ha:

K = 1 + 3.322 _* Logg₁₀ (N)

K = 1+3.322_* Logg (142)

K = 1+3.322_* 2.1523

K = 8,14 ≈ 8

Dermed vil distribusjonen være i 8 intervaller.

Antall intervaller må alltid være representert med hele tall. I tilfeller der verdien er desimal, må det gjøres en tilnærming til det nærmeste hele antallet.

Sturges regelapplikasjoner

Sturges -regelen brukes hovedsakelig i statistikk, siden den tillater en frekvensfordeling gjennom beregningen av antall klasser (k), så vel som lengden på hver av disse, også kjent som amplitude.

Amplituden er forskjellen i den øvre og nedre grensen for klassen, delt på antall klasser, og er uttrykt:

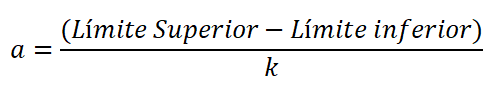
Det er mange empiriske regler som tillater en frekvensfordeling. Sturges -regelen brukes imidlertid ofte fordi den gjør en tilnærming av antall klasser, som vanligvis går fra 5 til 15.

På denne måten vurderer den en verdi som riktig representerer en prøve eller en populasjon; Det vil si at tilnærmingen ikke representerer ekstreme grupper, og fungerer heller ikke med et for stort antall klasser som ikke tillater å oppsummere prøven.

Det kan tjene deg: motsatte vinkler med toppunktet (med en løst øvelse)

Eksempel

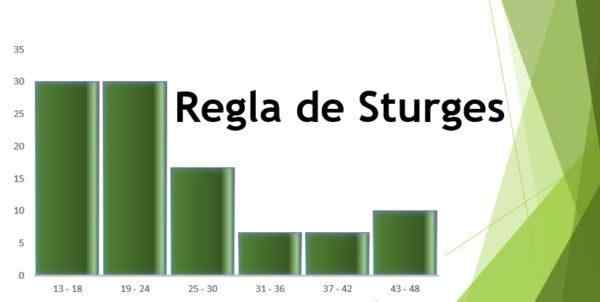
Et frekvenshistogram må utføres i henhold til de gitte dataene, som tilsvarer aldre oppnådd i en undersøkelse av menn som trener i en lokal gymsal.

For å bestemme intervallene, bør prøvestørrelsen eller antall observasjoner være kjent; I dette tilfellet er det 30.

Da gjelder Sturges -regelen:

K = 1 + 3.322 _* Logg₁₀ (N)

K = 1+3.322_* Logg (30)

K = 1+3.322_* 1.4771

K = 5,90 ≈ 6 intervaller.

Fra antall intervaller kan du beregne amplituden de vil ha; Det vil si at bredden på hver stolpe representert i frekvenshistogrammet:

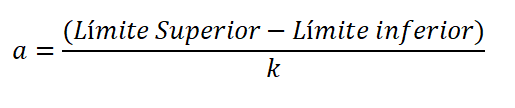
Den nedre grensen anses som den lavere verdien av dataene, og den øvre er den høyeste verdien. Forskjellen mellom øvre og nedre grense kalles området eller ruten til variabelen (R).

Tabellen har at den øvre grensen er 46 og de nedre 13; På den måten vil amplituden til hver klasse være:

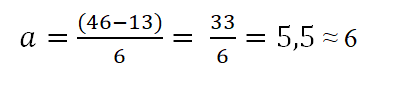
Intervallene vil være sammensatt av en øvre og nedre grense. For å bestemme disse intervallene begynner det med å telle fra den nedre grensen, og legge til dette amplituden som er bestemt av regel (6), som følger:

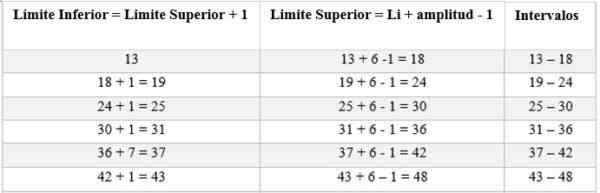
Deretter beregnes den absolutte frekvensen for å bestemme antall menn som tilsvarer hvert intervall; I dette tilfellet er det:

• Intervall 1: 13 - 18 = 9
• Intervall 2: 19 - 24 = 9
• Intervall 3: 25 - 30 = 5
• Intervall 4: 31 - 36 = 2
• Intervall 5: 37 - 42 = 2
• Intervall 6: 43 - 48 = 3

Ved å legge til den absolutte frekvensen for hver klasse, må dette være lik det totale antallet av prøven; I dette tilfellet 30.

Kan tjene deg: negativ homotecia

Deretter beregnes den relative frekvensen for hvert intervall, og deler den absolutte frekvensen av dette med det totale antall observasjoner:

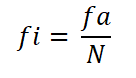
• Intervall 1: Fi = 9 ÷ 30 = 0,30
• Intervall 2: Fi = 9 ÷ 30 = 0,30
• Intervall 3: Fi = 5 ÷ 30 = 0.1666
• Intervall 4: fi = 2 ÷ 30 = 0,0666
• Intervall 5: Fi = 2 ÷ 30 = 0,0666
• Intervall 4: Fi = 3 ÷ 30 = 0,10

Deretter kan du lage en tabell som gjenspeiler dataene, og også diagrammet fra den relative frekvensen i forhold til de oppnådde intervallene, som det kan sees på følgende bilder:

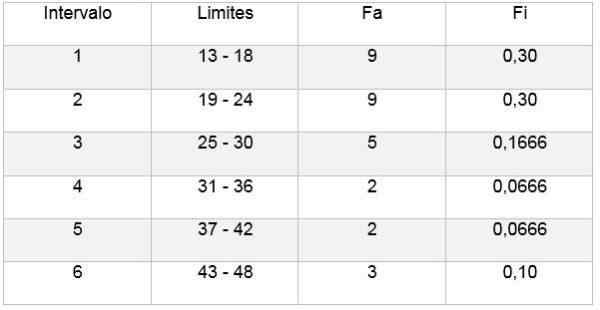
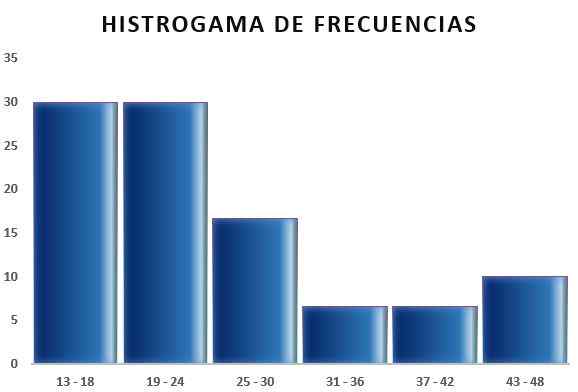
På denne måten tillater Sturges -regelen å bestemme antall klasser eller intervaller der en prøve kan deles, for å oppsummere en dataprøve gjennom utdyping av tabeller og grafikk.