Vektorer grafiske subs

De Vektor subtraksjon o vektor subtraksjon mellom vektorer eller og v betegnet av eller - v, Det beregnes ved å legge til vektoren eller med motsatt vektor v. Algebraisk er subtraksjonen uttrykt som følger:

eller - v = eller + (-v)

Det er mulig å utføre subtraksjon av vektorer etter forskjellige prosedyrer, for eksempel i grafisk form, på denne måten en vektor v Det er trukket av et orientert linjesegment -en pil-.

Lengden på pilen tilsvarer vektorkodulen, hellingen - angående en gitt referanselinje - indikerer retningen og enden indikerer retningen på vektoren.

Vektoren imot v Den har samme lengde og retning, men ellers. Deretter, før subtraksjonen mellom eller og v, Det er nødvendig å tegne den motsatte vektoren v, og legg til denne vektoren til deg.

Det er veldig viktig å understreke at subtraksjon av vektorer ikke er kommutativ, det vil si at rekkefølgen på vektorene endrer resultatet, derfor:

eller - v ≠ v - eller

Den grafiske prosedyren kan utføres ved hjelp av noen av disse metodene, hvis trinn vi vil forklare nedenfor:

-Trekantmetode.

-Parallellogrammetode.

[TOC]

Grafisk vektor sub -grafisk metode

Trekantmetode

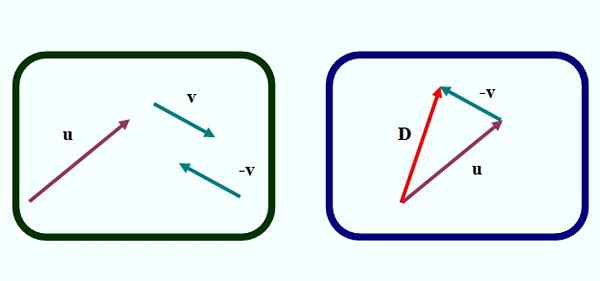
Figur 1. Vektorer underholdning i henhold til trekantmetoden. Kilde: f. Zapata.

I figur 1 har vi den første av metodene til å trekke fra to vektorer grafisk. Det handler om Trekantmetode, Fordi figuren som dannes når du etablerer vektorene, er en trekant, som vi kan se i venstre bilde.

Å trekke fra eller - v Vi fortsetter som følger:

-Tegn vektoren -v Fra vektoren v, ved oversettelse med regel og tropp, men endrer pilens retning (venstre bilde).

-Flytter til vektoren -v på en slik måte at opprinnelsen sammenfaller med slutten av vektoren eller (Høyre bilde).

Kan tjene deg: Friksjon: Typer, koeffisient, beregning, øvelser

-En vektor tegnes deretter (i rødt i riktig bilde) som går fra opprinnelsen til eller til slutten av v. Anrop D Og det er vektorforskjellen:

D = eller - v

Parallellogrammetode

I parallellogrammetoden må vektorene for å legge til eller trekke fra seg sammenfalle i sine opprinnelsespunkter. Anta at vi vil finne eller - v Med våre vektorer vist ovenfor, er trinnene for å finne subtraksjon av vektorer ved denne metoden følgende:

-Bestem den motsatte vektoren v, hva er -v, Som beskrevet før for trekantmetoden.

-Ta vektorene nøye eller og -v på en slik måte at dens opprinnelse sammenfaller.

-Nå er segmenterte parallelle linjer trukket fra endene av hver vektor. Figuren som er dannet er et parallellogram og i spesielle tilfeller der vektorene er vinkelrett på, er det et rektangel eller en firkant.

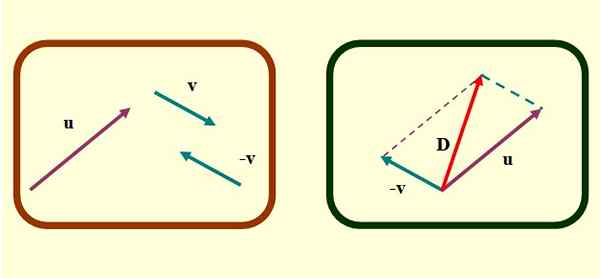Figur 2. Parallelogrammetode for vektorsubtraksjon. Kilde: f. Zapata.

-Endelig en vektor som starter fra den vanlige opprinnelsen til eller og v til slutten der de segmenterte parallelle linjene krysses. Dette er vektoren D eller subtraksjon.

Viktig

En annen måte å lage subtraksjon er å tegne parallellogrammet som om du ønsket å legge til vektorene.

Men i stedet for å tegne den vanlige diagonalen til summen, som går fra vanlig opprinnelse til skjæringspunktet mellom paralleller, Diagonal motsatt eller kortere, Som sett på figuren:

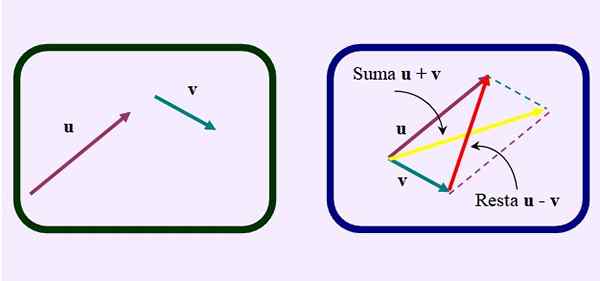Figur 3. En annen måte å utføre vektorsubtraksjon gjennom parallellogrammetoden. Kilde: f. Zapata.

Vektor subtraksjonseksempler

- Eksempel 1

Et skip navigerer i en elv og gjør det i motsatt retning av strømmen. En observatør på land observerer at skipets hastighet reduseres på grunn av virkningen av strømmen.

Kan tjene deg: hva med energien i materialene?

Hastigheten er en vektor, og i dette eksemplet peker hastigheten på skipet i en retning, og strømmen har samme retning og motsatt retning. Netthastigheten til skipet er summen av begge vektorene.

For eksempel, hvis instrumentene til fartøyet. Som V = V ' +VC, å være VC hastigheten på strømmen som beregnes ved subtraksjon av hastigheter V og V' henholdsvis: VC = V - V '= 30 km/h - 40 km/h = -10 km/ h.

- Eksempel 2

I kinematikk har vi viktige vektorer som beskriver endringer:

-Forskyvning for endringer i posisjon.

-Gjennomsnittlig hastighet, for å kvantifisere hvor raskt posisjonen varierer i tid.

-Akselerasjon, for hastighetsmodifikasjoner som en funksjon av tid.

Forskyvningsvektoren

Forskyvningsvektoren beskriver endringen i posisjon som en kropp opplever i løpet av bevegelsen.

La oss for eksempel se en partikkel som beskriver den flate banen vist på figuren, der den går fra punkt P₁ til punktet P₂.

Vektorene rettet fra opprinnelsen til X-Y-koordinatsystemet til disse punktene er posisjonsvektorene r₁ og r₂, Mens forskyvningsvektoren er Δr, alt fra s₁ A p₂. Det er sant, det:

Δr = r₂ - r₁

Derfor er forskyvningsvektoren subtraksjonen mellom den endelige posisjonsvektoren og startposisjonsvektoren, som bemerket av følgende figur. Enhetene er også de av stillingen: meter, føtter, miles, centimeter og mer.

Kan tjene deg: Perseus (Constellation): Plassering, mytologi og egenskaper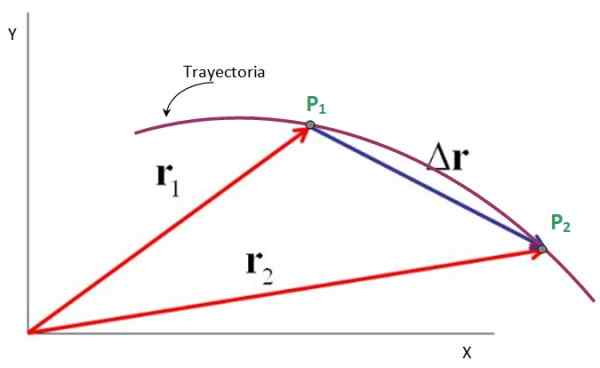Figur 4. Forskyvningsvektoren er forskjellen mellom den endelige og startposisjonen. Kilde: f. Zapata.

Gjennomsnittshastighet og gjennomsnittlig akselerasjonsvektorer

For sin del, gjennomsnittlig hastighetsvektor v_m Det er definert som forskyvningen multiplisert med det inverse av tidsintervallet:

 Og den gjennomsnittlige akselerasjonen er:

Trening løst

En partikkel som beskriver en sirkel tar 5 sekunder å gå fra punkt A til punkt B. I A har en hastighet v_TIL = 60 km/t mot +x og b -aksen er v_B = 60 km/t mot +og. Bestem den gjennomsnittlige akselerasjonen i grafisk og analytisk form.

Løsning

I grafisk bestemmes retning og betydning av gjennomsnittlig akselerasjon av:

I det følgende bildet er subtraksjon v_B - v_TIL, gjennom trekantmetoden, siden gjennomsnittlig akselerasjon til_m er proporsjonal med Δv. Trekanten dannet har de to kategoriene like, og derfor måler de akutte indre vinklene 45 º hver.

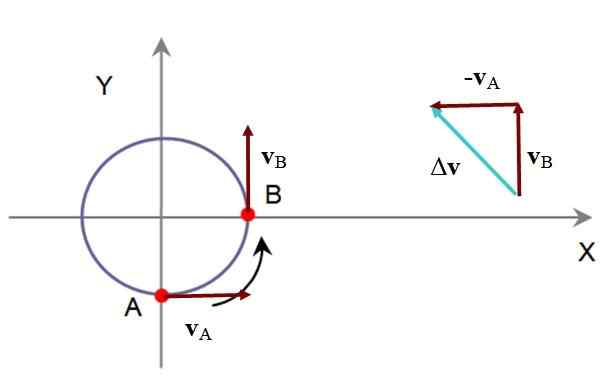Figur 5. Diagram over partikkelbevegelsen av det løste eksemplet. Kilde: f. Zapata.

Analytisk, hvis adresse +x sammenfaller med enhetsvektoren Yo og +-adressen og med enhetsvektoren J, så:

Δv = 60 km/t J - 60 km/t Yo

Tar ΔT = 5 s, i henhold til informasjonen i uttalelsen, er den gjennomsnittlige akselerasjonen:

til_m = (60 km/t J - 60 km/t Yo) / 5 s = 12 (J-Yo) Km/(h.s)

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley.
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
4. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.
6. Tipler, s. 2006. Fysikk for vitenskap og teknologi. 5. utg. Volum 1. Redaksjon tilbake.