Rett og semi -re -Rereed segment

En linje med linje og en semi -rett er differensiert i det faktum at linjesegmentet er begrenset; det vil si at deres første punkt og sluttpunkt er kjent. Fra semi -rettigheten er kjent dets første punkt, men ikke sluttpunktet, siden det strekker seg til uendelig.

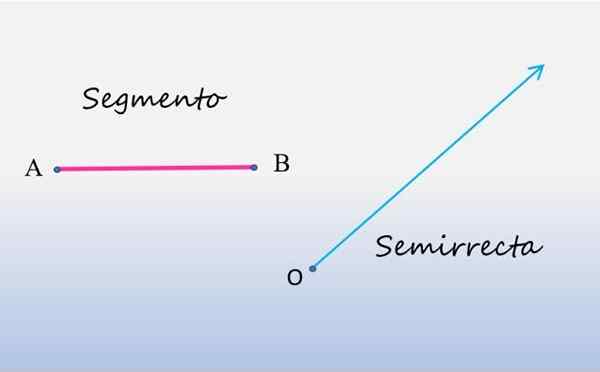
Følgende figur viser til venstre, et linjesegment, og til høyre, en halvrett:

Segment og semi -rett. Kilde: f. Zapata.

Som det kan sees, er segmentet en linje med linje, som begynner på punkt A og slutter på punkt B, disse punktene er endene på nevnte segment. Målingen av segmentet tilsvarer lengden mellom endene.

For sin del har semi -Right sitt utgangspunkt på punktet O og strekker seg til uendelig, noe som tilsvarer å si at det bare er begrenset i den ene enden, vanligvis kalt opprinnelse. Av denne grunn blir de også kalt God himmel.

Segmentene er betegnet gjennom bokstavene som indikerer det første punktet og slutten. For eksempel er segmentet av figuren segment AB, eller et slag plasseres på toppen, som dette:

På den annen side kan en halvgjenoppretting også utnevnes med to brev, en som indikerer punktet som tilsvarer opprinnelsen og et annet tilleggsbrev. Det kan også brukes et lite bokstav for å representere lynet eller semi -rekreasjons, og det er også semi -straks med sitt eget navn, som det vil bli sett i eksemplene senere.

Eksempler på segmenter

Segmentene er veldig viktige i geometri, nedenfor er noen av de mest bemerkelsesverdige:

Sider av en polygon

Polygonene er flate og lukkede figurer, hvis sider er ikke -samtykke linjesegmenter. For eksempel har en trekant tre sider, en firkantet har fire sider, en femkant har fem og så videre.

Det kan tjene deg: Tesseldos: Karakteristikk, typer (vanlig, uregelmessig), eksempler

Diameter på en omkrets

Det er definert som det segmentet som inneholder to punkter i omkretsen og passerer nødvendigvis gjennom sentrum av det samme.

Tau av en omkrets

Når et segment som blir med to punkter i omkretsen ikke går gjennom sentrum, kalles det tau.

Høyden på en trekant

Høyden på en trekant er definert som segmentet som går vinkelrett fra en av sidene av trekanten til motsatt toppunkt. Hvis målet på basen til en trekant, kalt B og høyden på det samme, betegnet som H er kjent, beregnes området A av det samme gjennom den velkjente formelen:

A = ½ b ∙ h

Semirret eksempler

Semi -Straight er også veldig viktige elementer i geometri. Noen velkjente semi -straks er:

De positive semi -Messages

De tre retningene i rommet: høy, bred og dybde kan representeres av et system med kartesiske akser, bestående av tre gjensidig vinkelrett linjer med hverandre, betegnet som akser x, og og z, som er kuttet på et punkt som heter opprinnelse.

Denne bestemmelsen deler plass inn i åtte regioner kjent som Octavers. I den følgende figuren blir de positive semi -dørene observert x, og og z, som bestemmer den første ocant. Tilsvarende bestemmer den positive semi -x y y regionen til flyet som kalles Første kvadrant.

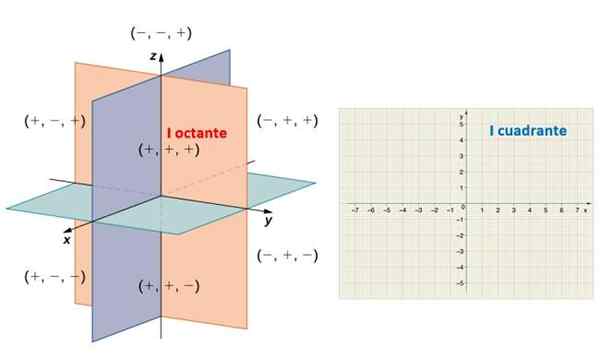På venstre side, de åtte oktantene av rom og til høyre, delte det kartesiske flyet i fire kvadranter. Kilde: Math Librettexts.

Sidene av en vinkel

En vinkel er brøkdelen av flyet som er avgrenset av to semi -straks hvis opprinnelse er vanlig. Dette punktet til felles er toppunkt av vinkelen, mens semi -straket kalles henholdsvis innledende side og sluttsiden av vinkelen. Slik bestemmelse vises i følgende figur:

Det kan tjene deg: Hva er forholdet mellom Rhombus -området og rektangelet?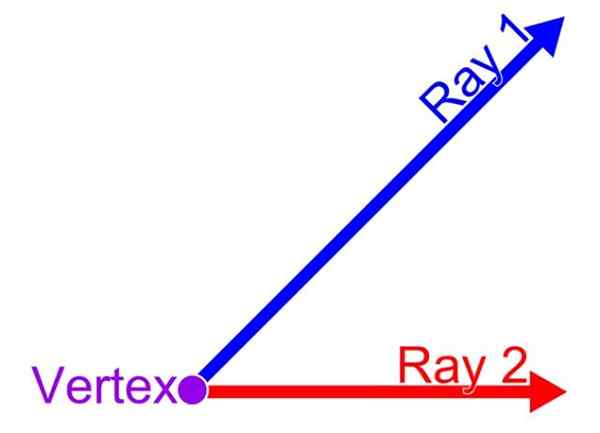 Elementer i en vinkel. Kilde: Wikimedia Commons.