Serie med makteksempler og øvelser

EN Power Series Den består av en sum av vilkår i form av krefter i variabelen x, eller mer generelt, av X-C, hvor c Det er et konstant reelt tall. I oppsummeringen av summen er det uttrykt en serie krefter som følger:

∑a_n (X -c)ⁿ = a_enten + til₁ (x - c) + a₂ (X - c)² + til₃ (X - c)³ +… + A_n (X - c)ⁿ

Hvor koeffisientene til_enten, til₁, til₂... de er reelle tall og serien begynner på n = 0.

Figur 1. Definisjon av en kraftserie. Kilde: f. Zapata.

Denne serien er fokusert på verdi c det er konstant, men du kan velge det c Være lik 0, i hvilket tilfelle kreftene er forenklet:

∑a_n xⁿ = a_enten + til₁ x + a₂ x² + til₃ x³ +… + A_n xⁿ

Serien begynner med til_enten(X-C)⁰ og til_entenx⁰ henholdsvis. Men vi vet det:

(X-C)⁰= x⁰ = 1

Derfor til_enten(X-C)⁰ = til_entenx⁰ = til_enten (Uavhengig betegnelse)

Det gode med kreftene i kreftene er at du med dem kan uttrykke funksjoner, og dette har mange fordeler, spesielt hvis du vil jobbe med en komplisert funksjon.

Når dette er tilfelle, i stedet for direkte å bruke funksjonen, brukes kraftutviklingen, noe som kan være lettere å utlede, integrere eller jobbe numerisk.

Selvfølgelig er alt betinget av konvergensen av serien. En serie konvergerer når ved å legge til en viss mengde vilkår, oppnås en fast verdi. Og hvis vi legger til flere vilkår, fortsetter vi å få den verdien.

[TOC]

Funksjoner som krefters krefter

Som et eksempel på en funksjon uttrykt som en serie med makt, la oss ta f (x) = e^x.

Denne funksjonen kan uttrykkes i form av en serie krefter som følger:

og^x  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) +..

Hvor! = n. (N-1). (N-2). (N-3) ... og det er tatt 0! = 1.

Vi kommer til å sjekke med hjelp av en kalkulator, som serien effektivt sammenfaller med den eksplisitt gitte funksjonen. La oss for eksempel begynne å gjøre x = 0.

Kan tjene deg: Teoretisk sannsynlighet: Hvordan få det ut, eksempler, øvelser

Vi vet at E⁰ = 1. La oss se hva serien gjør:

og⁰ ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +... = 1

Og la oss nå prøve med x = 1. En kalkulator kaster det og¹ = 2.71828, Og så la oss sammenligne med serien:

og¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) + ... = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +... ≈ 2.7167

Med bare 5 begreper har vi allerede nøyaktig tilfeldighet i E ≈ 2.71. Serien vår mangler bare litt mer, men etter hvert som flere vilkår er lagt til, konvergerer serien til den nøyaktige verdien av og. Representasjonen er nøyaktig når N → ∞.

Hvis den forrige analysen gjentas for n = 2 Veldig like resultater oppnås.

På denne måten er vi sikre på at eksponentiell funksjon f (x) = e^x Det kan være representert av denne kreftens serie:

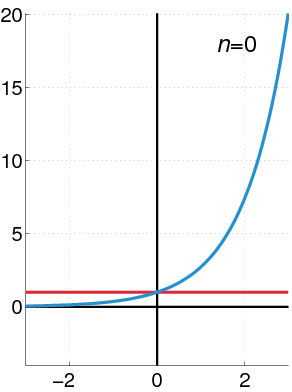Figur 2. I denne animasjonen blir det sett på som kreftene er nærmere eksponentiell funksjon ettersom flere begreper blir tatt. Kilde: Wikimedia Commons.

Geometriske krefter av krefter

Funksjonen f (x) = e^x Det er ikke den eneste funksjonen som innrømmer en seriell representasjon av krefter. For eksempel funksjonen  F(x) = 1/1 - x  Det ser mye ut som den kjente Konvergent geometrisk serie:

∑a.rⁿ = A / 1 - r

Bare gjør a = 1 og r = x for å få en passende serie til denne funksjonen, som er sentrert på C = 0:

Imidlertid er det kjent at denne serien er konvergent for │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Når du vil definere denne funksjonen i et annet intervall, fokuserer den ganske enkelt på en tilstrekkelig verdi og klar.

Hvordan finne serieutviklingen av krefter til en funksjon

Enhver funksjon kan utvikles i en serie krefter fokusert på C, så lenge du har avledet fra alle ordrer ved x = C. Prosedyren benytter seg av følgende teorem, kalt Taylor Teorem:

La f (x) være en funksjon med ordresederivater n, betegnet som F^(N), som innrømmer en serieutvikling av krefter i intervallet Yo. Dens utvikling i Taylor Series er:

Det kan tjene deg: Hva er stedet for hele og desimaltall?

Så det:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² /2 + f "(c) (x-c)³ /6 +… r_n

Hvor r_n, som er den første i serien, kalles den rest:

Når C = 0 kalles serien Maclaurin -serien.

Denne serien som er gitt her er identisk med serien gitt i begynnelsen, først nå er det en måte å eksplisitt finne koeffisientene til hvert begrep, gitt av:

Imidlertid må det sikres at serien formidler funksjonen du vil representere. Det hender at ikke alle Taylor -serier nødvendigvis konvergerer til F (x) som var i tankene når de beregnet koeffisientene til_n.

Dette skjer fordi kanskje de som er avledet fra funksjonen, evaluert i x = c sammenfalle med samme verdi av de som er avledet fra en annen, også i x = c. I dette tilfellet ville koeffisientene være de samme, men utviklingen ville være tvetydig ved ikke å ha sikkerheten om hvilken funksjon som tilsvarer.

Heldigvis er det en måte å vite på:

Konvergenskriterier

For å unngå tvetydighet, hvis r_n → 0 Når n → ∞ for alle x i intervall I, konvergerer serien til F (x).

Trening

- Trening løst 1

Finn de geometriske kreftene for funksjon f (x) = 1/2 - x fokusert på c = 0.

Løsning

Den gitte funksjonen må uttrykkes på en måte som samsvarer så mye som mulig med 1 / 1- x, hvis serie er kjent. Derfor skriver vi om teller og nevner, uten å endre det opprinnelige uttrykket:

1/2 - x = (1/2) / [1 - (x / 2)]]

Ettersom ½ er konstant, går den ut av summen, og dette er skrevet i form av den nye variabelen X/2:

Kan tjene deg: konjugert binomial: hvordan det løses, eksempler, øvelser

Merk at x = 2 ikke tilhører funksjonens domene, og i henhold til konvergenskriteriene gitt i seksjonen Power Geometric Series, Utviklingen er gyldig for │x/2│< 1 o equivalentemente -2 < x < 2.

- Trening løst 2

Finn de første 5 begrepene i MacLaurins serieutvikling av funksjonen f (x) = sen x.

Løsning

Trinn 1

Først er derivatene:

-Avledet fra orden 0: Det er den samme funksjonen f (x) = sen x

-Første derivat: (sin x) '= cos x

-Andre derivat: (sin x) "= (cos x) '= - sin x

-Tredje derivat: (sin x) "= (-sen x) '= - cos x

-Fjerde derivat: (sin x) "= (- cos x) '= sin x

Steg 2

Deretter blir hvert derivat evaluert ved x = c, som en utvikling av maclaurin, c = 0:

sin 0 = 0; cos 0 = 1; - Sen 0 = 0; -Kos 0 = -1; sin 0 = 0

Trinn 3

Koeffisientene er bygget til_n;

til_enten = 0/0! = 0; til₁ = 1 /1! = 1; til₂ = 0 /2! = 0; til₃ = -1 / 3!; til₄ = 0/4! = 0

Trinn 4

Endelig er serien samlet i henhold til:

sin x ≈ 0.x⁰ + 1. x¹ + 0 .x² - (1/3!) x³ + 0.x⁴... = x - (1/3!)) x³  +..

Trenger leseren flere vilkår? Hvor mange flere, serien er nærmere funksjonen.

Legg merke til at det er et mønster i koeffisientene, følgende ikke -null -begrepet er å₅ Og all den rare indeksen er også forskjellig fra 0, veksler skiltene, slik at:

Sen X ≈ X - (1/3!)) x³  + (1/5!)) x⁵ - (1/7!)) x⁷  +.. .

Det er igjen som trening å bekrefte, du kan bruke forholdet mellom kvotienten For seriekonvergens.

Referanser

1. CK-12 Foundation. Power Series: Representasjon av funksjoner og operasjoner. Gjenopprettet fra: CK12.org.
2. Engler, a. 2019. Integrert beregning. National University of the Coast.
3. Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.
4. Gratis matematikkekster. Power Series. Gjenopprettet fra: Matematikk.Liibretexts.org.
5. Wikipedia. Power Series. Gjenopprettet fra: er.Wikipedia.org.