Oktalt system

Hva er et oktalt system?

Han Oktalt system Det er et basetallingssystem åtte (8); Det vil si at den består av åtte sifre, som er: 0, 1, 2, 3, 4, 5, 6 og 7. Derfor kan hvert siffer på et oktalt tall ha noen verdi fra 0 til 7. Oktale tall dannes fra binære tall.

Dette er fordi basen er en eksakt kraft på to (2). Det vil si at tallene som tilhører oktalsystemet dannes når de er gruppert i tre sifre på rad, bestilt fra høyre til venstre, og dermed oppnå desimalverdien.

Historien om oktalsystemet

Oktalsystemet har sin opprinnelse i eldgamle tider, da folk brukte hendene til å telle åtte av åtte dyr.

For å telle antall kyr i en stall, begynte for eksempel høyre hånd å ha tommelen med lillefingeren; For å telle det andre dyret, kom tommelen sammen med pekefingeren, og så videre med de gjenværende fingrene på hver hånd, til den er fullført 8.

Det er muligheten for at oktalnummereringssystemet før desimalen skal kunne telle de interdigitale rommene; det vil si, fortell alle fingrene bortsett fra tommelen.

Deretter ble oktalnummereringssystemet etablert, som stammet fra det binære systemet, fordi det trenger mange sifre for å representere bare ett tall; Fra da av ble det opprettet oktale og sekskantede systemer, som ikke krever så mange sifre og som lett kan konvertere til det binære systemet.

Oktalt nummereringssystem

Oktalsystemet består av åtte sifre fra 0 til 7. Disse har samme verdi som for desimalsystemet, men deres relative verdi endres avhengig av posisjonen som disse okkuperer. Verdien av hver stilling er gitt av basen Powers 8.

Det kan tjene deg: Regel T: Karakteristikker, slik at det er eksempler

Posisjonene til sifrene i et oktalt nummer har følgende pesos:

8⁴, 8³, 8², 8¹, 8⁰, Octal Point, 8^-1, 8^-2, 8^-3, 8^-4, 8^-5.

Det viktigste oktalsifret er 7; På denne måten, når det telles i dette systemet, øker en plassering av et siffer fra 0 til 7. Når den når 7, blir den resirkulert til 0 for neste telling; Dette øker følgende sifferposisjon. For eksempel for å telle sekvenser, i oktalsystemet, vil det være:

• 0, 1, 2, 3, 4, 5, 6, 7, 10.
• 53, 54, 55, 56, 57, 60.
• 375, 376, 377, 400.

Det er en grunnleggende teorem som brukes på oktalsystemet, og uttrykkes som følger:

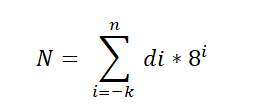
I dette uttrykket representerer Di sifferet multiplisert med basen 8 -strømmen, noe som indikerer posisjonsverdien til hvert siffer, på samme måte som det er bestilt i desimalsystemet.

For eksempel har du nummer 543.2. For å ta det til oktalsystemet, dekomponerer det som følger:

N = ∑ [(5 _* 8²) + (4 _* 8¹) + (3 _*8⁰) + (2 _*8^-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0.125)

N = 320 +32 + 2 + 0,25 = 354 + 0,25_d

På den måten har du 543.2_q = 354.25_d. Abonnementet som indikerer at det er et oktalt tall som også kan representeres med nummer 8; og abonnement D refererer til desimaltallet, som også kan være representert med nummer 10.

Oktal systemkonvertering til desimal

For å konvertere et oktalt systemnummer til tilsvarende til desimalsystemet, må hvert oktalt siffer multipliseres med posisjonsverdien, fra høyre.

Eksempel 1

732₈ = (7_* 8²) + (3_* 8¹) + (2_* 8⁰) = (7 _* 64) + (3 _* 8) + (2 _* 1)

732₈= 448 +24 +2

732₈= 474₁₀

Kan tjene deg: matematisk likhet

Eksempel 2

26.9₈ = (2 _*8¹) + (6_* 8⁰) + (9_* 8^-1) = (2 _* 8) + (6 _* 1) + (9 _* 0.125)

26.9₈ = 16 + 6 + 1.125

26.9₈= 23,125₁₀

Desimalsystemkonvertering til oktal

Et desimaltall kan konverteres til et oktalt tall ved bruk av den gjentatte divisjonsmetoden, der desimal heltallet er delt med 8 til kvotienten er lik 0, og avfallet til hver divisjon vil representere oktalt antall.

Avfallet bestilles fra den siste til den første; det vil si at den første resten vil være det minst betydningsfulle sifferet i oktaltallet. På denne måten vil det mest betydningsfulle sifferet være den siste resten.

Eksempel

Octal of the desimal nummer 266₁₀

- Desimal nummer 266 er delt med 8 = 266/8 = 33 + 2 rest.

- Da er 33 delt med 8 = 33/8 = 4 + 1 rest.

- 4 er delt med 8 = 4/8 = 0 + 4 rest.

Som med den siste divisjonen en kvotient mindre enn 1 oppnås, betyr det at resultatet er funnet; Bare restene må bestilles omvendt, slik at oktalt antall desimaler 266 er 412, som det kan sees i følgende bilde:

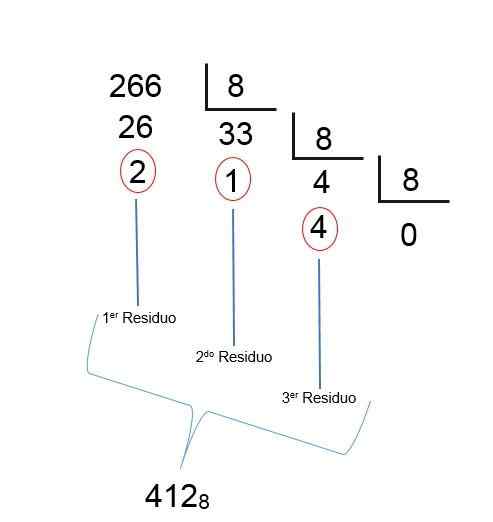
Binær oktal systemkonvertering

Konverteringen av oktal til binærsystem utføres når du konverterer oktalsifret til det tilsvarende binære sifferet, dannet av tre sifre. Det er et bord som viser hvordan de åtte mulige sifrene blir:

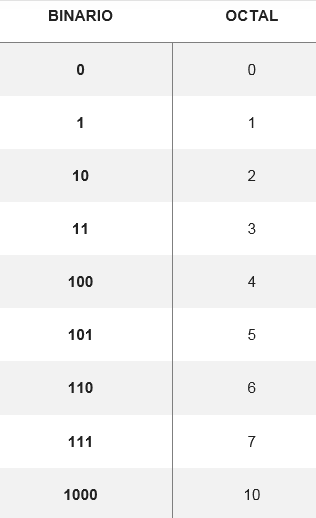
Fra disse konverteringene kan du endre et hvilket som helst antall oktalsystem til binær, for eksempel å konvertere nummer 572₈ Ekvivalenter er søkt i tabellen. Dermed må du:

5₈ = 101

7₈= 111

2₈ = 10

Derfor 572₈ tilsvarende i det binære systemet til 10111110.

Binært system til oktal konvertering

Prosessen med konvertering av integrerte tall til oktale heltall er omvendt operasjon til forrige prosess.

Kan tjene deg: Hva er elementene i en vinkel?

Det vil si at binære tallbiter er gruppert i to grupper på tre biter, fra høyre til venstre. Deretter blir binær til oktal konvertering gjort med forrige tabell.

I noen tilfeller vil det binære antallet ikke ha grupper på 3 biter; For å fullføre det, blir en eller to nuller lagt til venstre for den første gruppen.

For å endre det binære nummeret 11010110 til oktal gjøres følgende for eksempel:

- Grupper på 3 biter dannes fra høyre (siste bit):

11010110

- Ettersom den første gruppen er ufullstendig, legges en null til venstre:

011010110

- Konverteringen er laget av tabellen:

011 = 3

010 = 2

110 = 6

På denne måten tilsvarer binært nummer 011010110 326₈.

Konvertering av oktalsystemet til heksadesimal og omvendt

For å endre et oktalt tall til heksadesimal eller heksadesimal til oktalt system, er det nødvendig at antallet først vil være binært, og deretter til ønsket system.

For dette er det et tabell der hvert heksadesimal siffer er representert med ekvivalensen i det binære systemet, sammensatt av fire sifre.

I noen tilfeller vil det binære antallet ikke ha grupper på 4 biter; For å fullføre det, blir en eller to nuller lagt til venstre for den første gruppen

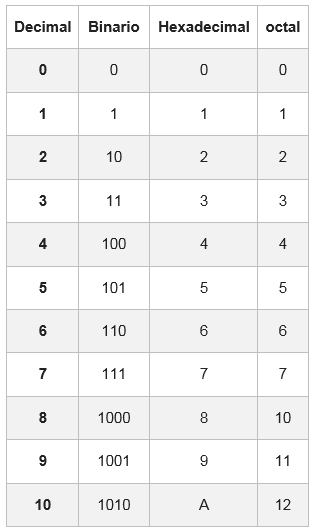
Eksempel

Konverter 1646 oktale nummer til et heksadesimalt nummer:

- Oktal til binært nummer blir

1₈ = 1

6₈ = 110

4₈ = 100

6₈ = 110

- Dermed 1646₈ = 1110100110.

- For å konvertere fra binær til heksadesimal blir de først bestilt i en gruppe på 4 biter, fra høyre til venstre:

11 1010 0110

- Den første gruppen er fullført med nuller, slik at den kan ha 4 biter:

0011 1010 0110

- Heksadesimal binær systemkonvertering er gjort. Ekvivalensene erstattes av tabellen:

0011 = 3

1010 = a

0110 = 6

På denne måten tilsvarer Octal -tallet fra 1646 3A6 i heksadesimalsystemet.