Sum av polynomer, som gjøres, eksempler, øvelser

De Sum av polynomer Det er operasjonen som består i å legge til to eller flere polynomer, noe som resulterer i et annet polynom. For å utføre det er det nødvendig å legge til vilkårene i samme rekkefølge for hver av polynomene og indikere den resulterende summen.

Først gjennomgår vi kort betydningen av "vilkårene for samme ordre". En noens polynom består av summer og/eller subtraksjon av begreper.

Figur 1. For å legge til to polynomer er det nødvendig å bestille dem og deretter redusere de lignende vilkårene. Kilde: Pixabay + Wikimedia Commons.

Begrepene kan være produkter med reelle tall og en eller flere variabler, representert med bokstaver, for eksempel: 3x² og -√5.til²BC³ De er vilkår.

Vel, vilkårene i samme rekkefølge er de som har samme eksponent eller kraft, selv om de kan ha forskjellige koeffisienter.

-Vilkår for lik orden er: 5x³, √2 x³ og -1/2x³

-Ulike ordrer vilkår: -2x^-2, 2xy^-1 og √6x²og

Det er viktig å huske på at bare vilkårene i samme ordre kan legges til eller trekkes fra, en operasjon som er kjent som reduksjon. Ellers er summen ganske enkelt angitt.

Når begrepet vilkår i samme rekkefølge er avklart, blir polynomene lagt til etter disse trinnene:

-Rekkefølge Først polynomene å legge til, alt på samme måte, enten øker eller synker, det vil si med kreftene fra minst til største eller omvendt.

-Å fullføre, I tilfelle noen kraft i sekvensen mangler.

-Redusere De lignende vilkårene.

-Indikerer Den resulterende summen.

[TOC]

Polynomsumseksempler

Vi starter med å legge til to polynomer med en enkelt variabel kalt x, For eksempel polynomene P (x) og Q (x) gitt av:

P (x) = 2x² - 5x⁴ + 2x -x⁵ - 3x³ +12

Q (x) = x⁵- 25 x + x²

Etter de beskrevne trinnene begynner det med å bestille dem avtagende, noe som er den mest vanlige måten:

P (x) = -x⁵- 5x⁴  - 3x³  + 2x² + 2x +12

Det kan tjene deg: Innskrevet vinkel på en sirkel: Definisjon, teoremer, eksempler

Q (x) = x⁵+ x² - 25x

Polynom q (x) er ikke fullstendig, det ser at krefter med eksponent 4, 3 og 0. Sistnevnte er ganske enkelt det uavhengige begrepet, den som ikke har noe brev.

Q (x) = x⁵+ 0x⁴ + 0x³ + x² - 25x + 0

Når dette trinnet er ferdig, er de klare til å legge til. Du kan legge til de lignende begrepene og deretter angi summen, eller plassere polynomene som er bestilt av hverandre og redusere med kolonner, på denne måten:

- x⁵ - 5x⁴  - 3x³ + 2x² + 2x +12

+ x⁵ + 0x⁴ + 0x³  +  x²  - 25x + 0     +

--

0x⁵-5x⁴ - 3x³  +3x² - 23x + 12 = P (x) + q (x)

Det er viktig å merke seg at når det er lagt til, gjøres det algebraisk å respektere tegnregelen, på denne måten 2x + (-25 x) = -23x. Det vil si at hvis koeffisientene har forskjellige tegn, blir trukket fra og resultatet bærer tegnet på hovedfaget.

Legg til to eller flere polynomer med mer enn en variabel

Når det gjelder polynomer med mer enn en variabel, er en av dem valgt å bestille den. Anta for eksempel at det blir bedt om å legge til:

R (x, y) = 5x²  - 4y² +  8xy - 6y³ 

OG:

T (x, y) = ½ x²- 6y²  - 11xy + x³og

En av variablene er valgt, for eksempel X til bestilling:

R (x, y) = 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy - 6y² 

De manglende vilkårene er umiddelbart fullført, hvor hvert polynom har:

R (x, y) = 0x³og + 5x² +  8xy - 6y³  - 4y²

T (x, y) = + x³y + ½ x² - 11xy + 0y³ - 6y² 

Og begge er klare til å redusere lignende vilkår:

0x³og + 5x² +  8xy - 6y³  - 4y²

Kan tjene deg: Bestemmelseskoeffisient: Formler, beregning, tolkning, eksempler

+ x³y + ½ x² - 11xy + 0y³ - 6y²       +

-

+ x³Y + 11/2x² - 3xy - 6y³  - 10y²    = R (x, y) + t (x, y)

Polynomsumøvelser

- Oppgave 1

I den neste summen av polynomer, indikerer begrepet som må gå i blanket for å oppnå polynomsummen:

-5x⁴  + 0x³ +  2x²         + 1

x⁵  + 2x⁴             - 21x² + 8x - 3

2x⁵             +9x³             -14x

-

-6x⁵+10x⁴ -0x³  + 5x²   - 11x + 21

Løsning

Å få -6x⁵ Det kreves en betegnelse på AX -formen⁵, slik at:

A + 1+ 2 = -6

Derfor:

A = -6-1-2 = -9

Og begrepet søkte er:

-9x⁵

-Fortsett på en lignende måte for å finne resten av vilkårene. Her er Exponent 4:

-5 + 2 + A = 10 → A = 10 + 5-2 = 13

Det manglende begrepet er: 13x⁴.

-For x krefter³ Det er umiddelbart at begrepet må være -9x³, På denne måten er den kubiske termkoeffisienten 0.

-Når det gjelder kvadratkakene: a + 8 -14 = -11 → a = -11 -8 + 14 = -5 og begrepet er -5x².

-Det lineære begrepet oppnås med en +8 -14 = -11 → A = -11 + 14 -8 = -5, og er det manglende begrepet -5x.

-Til slutt er det uavhengige uttrykket: 1 -3 + A = -21 → A = -19.

- Oppgave 2

Et flatt terreng er omgitt som vist på figuren. Finn et uttrykk for:

a) Omkretsen og

b) Området, med tanke på de angitte lengdene:

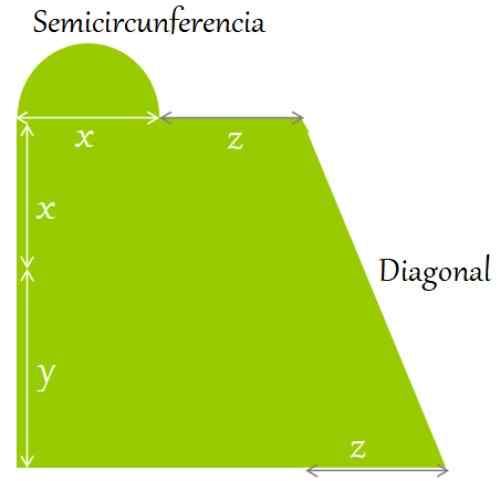Figur 2. Et flatt terreng er omgitt av form og dimensjoner indikert. Kilde: f. Zapata.

Løsning på

Omkretsen er definert som summen av sidene og konturene på figuren. Fra og med nedre venstre hjørne, i retning av klokkehender, har du:

Det kan tjene deg: Isosceles trapesoid: egenskaper, forhold og formler, eksempler

Omkrets = y + x + halvsirkel lengde + z + Diagonal lengde + Z + z + x

Halvsirkelen har en diameter lik x. Ettersom radius er halvparten av diameteren, må den:

Radio = x/2.

Formelen for lengden på en komplett omkrets er:

L = 2π x radio

Så:

Halvsirkel lengde = ½. 2π (x/2) = πx/2

For sin del beregnes diagonalen med Pythagoras -teoremet påført på sidene: (x+y) som er vertikal side og z, som er horisontalt:

Diagonal = [(x+y)² + z²]^1/2

Disse uttrykkene erstattes i omkretsen for å oppnå:

Omkrets = y + x + πx/2 + z + [(x + y)² + z²]^1/2+ z + x + z

Lignende vilkår reduseres, siden summen krever at resultatet blir forenklet maksimalt:

Omkrets = y + [x + π (x/2) + x] + z + z + z + [(x + y)² + z²]^1/2 = y + (2 + π /2) x + 3z

Løsning b

Det resulterende området er summen av rektangelområdet, halvsirkelen og høyre trekant. Formlene for disse områdene er:

-Rektangel: Base x høyde

-Halvsirkel: ½ π (radio)²

-Triangel: Base x høyde /2

Rektangelområdet

(x+y). (x+z) = x² + Xz + yx + yz

Halvsirkelområde

½ π (x/2)² = π x² / 8

Området til trekanten

½ z (x + y) = ½ zx + ½ zy

Totalt areal

For å finne det totale arealet blir uttrykkene som er funnet for hvert delvis område lagt til:

Totalt areal = x² + Xz + yx + yz + (π x² / 8) + ½ ZX + ½ zy

Og til slutt alle vilkårene som er like:

Totalt areal = (1 + π/8) x² + 3/2 xy + 3/2yz + yx

Referanser

1. Baldor, a. 1991. Algebra. Venezuelansk kulturell redaksjon S.TIL.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Matematikk er morsomt. Legge og subtraksjonspolynomer. Gjenopprettet fra: matematikk.com.
4. Monterey Institute. Legge til og trekke fra polynomer. Gjenopprettet fra: MontereyInstitute.org.
5. UC Berkeley. Algebra av polynomer. Gjenopprettet fra: Matematikk.Berkeley.Edu.