Teori om sett egenskaper, elementer, eksempler, øvelser

De sett teori Det er en gren av den logikk-matematikken som er ansvarlig for studiet av forhold mellom enheter som kalles sett. Settene er preget av å være samlinger av objekter av samme natur. Disse objektene er elementene i settet og kan være: tall, bokstaver, geometriske figurer, ord som representerer objekter, gjenstandene i seg selv og andre.

Det var Georg Cantor, mot slutten av 1800 -tallet, som foreslo settet med sett. Mens andre bemerkelsesverdige matematikere i det tjuende århundre gjorde sin formalisering: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel blant andre.

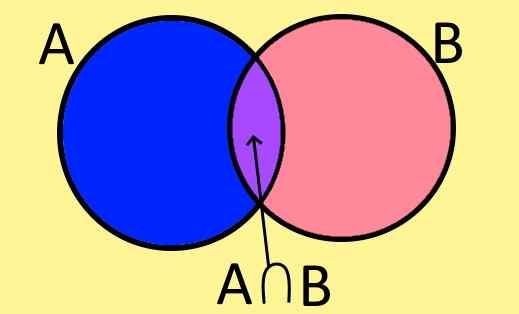
Figur 1. Venn Diagram of Sets A, B og deres kryss A⋂ B. (Egen utdyping).

Venn -diagrammer er den grafiske måten å representere et sett, og består av en lukket flat figur som elementene i settet er.

For eksempel viser figur 1 to sett A og B, som har elementer til felles, elementene som er felles for A og B. Disse danner et nytt sett kalt krysset med A og B, som er skrevet symbolsk som følger:

A ∩ B

[TOC]

Kjennetegn

Settet er et primitivt konsept som det er i geometri begrepet punkt, rett eller flat. Det er ingen bedre måte å uttrykke konseptet på enn å påpeke eksempler: 

Settet og dannet av fargene på Spanias flagg. Denne måten å uttrykke settet kalles av forståelse. Det samme settet og skrevet av forlengelse er:

E = rød, gul

I dette tilfellet er rødt og gult elementer i settet og. Det skal bemerkes at elementene er oppført mellom nøklene og ikke gjentas. Når det.

Anta at Sett V ble dannet av de tre første vokalbrevene:

V = a, e, i

Kraften til V, som er betegnet med P (V) er settet med alle settene som kan dannes med elementene i V:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Typer sett

Endelig sett

Det er et sett der elementene er tallrike. Eksempler på endelige sett er bokstavene i det spanske alfabetet, spanskens vokaler, blant annet planetene til solsystemet. Antall elementer i et begrenset sett kalles kardinaliteten.

Uendelig sett

Uendelig ensemble, alle som antall elementer er uontable, siden uansett hvor stort antall elementer alltid er mulig å finne flere elementer.

Et uendelig setteksempel er settet med naturlige tall n, som er omfattende uttrykt som følger:

Kan tjene deg: Coplanares Points: Ligning, eksempel og løste øvelser

N = 1, 2, 3, 4, 5, .. . er helt klart et uendelig sett, siden det ikke spiller noen rolle hvor stort et naturlig tall kan være, kan følgende hovedfag alltid finne i en uendelig prosess. Det er klart at kardinaliteten til et uendelig sett er ∞.

Tomt sett

Det er settet som ikke inneholder noe element. Det tomme settet V er betegnet med Ø eller ved hjelp av et par nøkler uten elementer inne:

V = = Ø.

Det tomme settet er unikt, derfor må det være feil å si "et tomt sett", riktig form er å si "det tomme settet".

Blant egenskapene til det tomme settet er det at det er undergruppe av ethvert sett:

Ø ⊂ a

I tillegg, hvis et sett er undergruppe av det tomme settet, vil dette settet nødvendigvis være tomrommet:

A ⊂ Ø ⇔ A = Ø

Enhetlig sett

Det kalles enhetssettet et hvilket som helst sett som inneholder et enkelt element. For eksempel er settet med naturlige satellitter på jorden et enhetssett, hvis eneste element er månen. Sett B av hele tall mindre enn 2 og større enn null har bare element 1, derfor er det et enhetssett.

Binær sett

Et sett er binært hvis det bare har to elementer. For eksempel sett x, slik at x er et reelt antall x^2 = 2 = 2. Dette settet i forlengelse er skrevet slik:

X = -√2, +√2

Universelt sett

Det universelle settet er et sett som inneholder andre sett av samme type eller natur. For eksempel er det universelle settet med naturlige tall settet med reelle tall. Men reelle tall er også universelle av hele tall og rasjonelle tall.

Kjerneartikler

- Forhold mellom sett

I settene kan du etablere flere typer forhold mellom dem og deres elementer. Hvis to sett A og B har nøyaktig de samme elementene, er et likeverdig forhold betegnet som følger:

TIL = B

Hvis alle elementene i et sett til å tilhøre et sett B, men ikke alle elementene i B tilhører A, er det blant disse settene et inkluderingsforhold som er betegnet som følger:

A ⊂ b, men b ⊄ a

Det forrige uttrykket lyder: a er delmengde av b, men b er ikke delmengde av en.

For å indikere at noen eller noen elementer tilhører et sett, brukes symbolet på tilhørighet ∈, for eksempel for å si at X -element eller elementer tilhører settet A er skrevet symbolsk som følger:

x ∈ A

Ja et element og tilhører ikke settet til dette forholdet er skrevet slik:

og ∉ a

Tilhørighetsforholdet er gitt mellom elementene i et sett og settet, med det eneste unntak av kraftsettet, settet er samlingen eller settet med alle mulige sett som kan dannes med elementene i nevnte sett.

Kan tjene deg: faktorisering

Anta v = a, e, i, kraften din er p (v) = a, e, i, a, e, a, i, e, i, A, E, I, i så fall blir settet V et element i settet P (V) og kan skrives:

V ∈ P (v)

- Inkluderingsegenskaper

Den første egenskapen til inkludering slår fast at hvert sett er inneholdt i seg selv, eller med andre ord, som er undergruppe av seg selv:

A ⊂ a

Den andre egenskapen til inkludering er transitivitet: Hvis a er delmengde av B og B på sin side, er det undergruppe av C, da er A delmengde av C. Symbol som transitivitetsforholdet er skrevet slik:

(A ⊂ B) ^ (B ⊂ C) => A ⊂ C

Nedenfor er Venn -diagrammet som tilsvarer transitiviteten til inkludering:

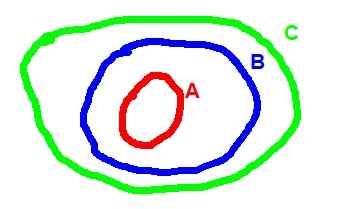Figur 2. (A ⊂ B) ^ (B ⊂ C) => A ⊂ C

- Operasjoner mellom settene

Kryss

Krysset er en operasjon mellom to sett som resulterer i et nytt sett som tilhører det samme universelle settet av de to første. I den forstand er det en lukket operasjon.

Symbolisk er kryssingsoperasjonen formulert som følger:

A⋂b = x / x∈A ^ x∈B

Et eksempel er som følger: sett a av bokstavene i ordet "elementer" og sett B på bokstavene i ordet "gjentatt", er skjæringspunktet mellom A og B skrevet slik:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . Det universelle settet med A, fra B og også av A⋂B er settet med bokstavene i det spanske alfabetet.

Union

Foreningen av to sett er settet som er dannet av elementene som er felles for de to settene og de ikke -vanlige elementene i de to settene. Unionens operasjon mellom settene uttrykkes symbolsk som følger:

A∪b = x/x∈A v x∈B

Forskjell

Operasjonen av settet i det minste er settet betegnet med A-B. A-B er et nytt sett dannet av alle elementene som er i A, og som ikke tilhører B. Symbolet er skrevet slik:

A - b = x/ x ∈ A ^ x ∉ b

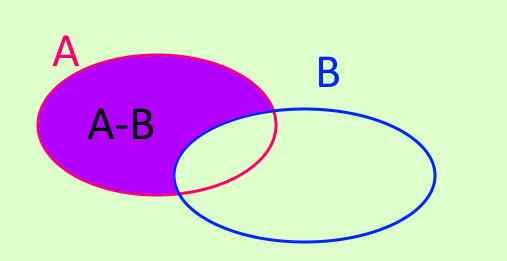Figur 3. A - b = x/ x ∈ A ^ x ∉ b

Symmetrisk forskjell

Den symmetriske forskjellen er en operasjon mellom to sett der det resulterende settet består av elementene som ikke er vanlig for de to settene. Den symmetriske forskjellen symbolsk er representert som følger:

A⊕b = x/ x∈ (a-b) ^ x∈ (b-a)

Eksempler

Eksempel 1

Venn -diagrammet er en grafisk måte å representere settene. For eksempel er sett C for bokstavene i ordsettet representert som følger:

Eksempel 2

Det er vist nedenfor gjennom Venn -diagrammer som, settet med vokaler i ordet "sett", er en delmengde av settet med bokstavene i ordet "sett".

Kan tjene deg: Kvoteprøvetaking: Metode, fordeler, ulemper, eksempler

Eksempel 3

Sett Ñ Fra bokstavene i det spanske alfabetet er det et begrenset sett, dette settet i forlengelsen er skrevet slik:

Ñ = A, B, C, D, E, F, G, H, I, J, K, L, M, N, ñ, O, P, Q, R, S, T, U, V, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, W, X, Y, Z og dets Kardinalitet er 27.

Eksempel 4

Sett V Fra vokalene på spansk er det en delmengde av ñ -settet:

V ⊂ Ñ Derfor er det et begrenset sett.

Det endelige settet V Utvidet måte det er skrevet slik: V = a, e, i, o, u og dets kardinalitet er 5.

Eksempel 5

Gitt settene A = 2, 4, 6, 8 og B = 1, 2, 4, 7, 9 Bestem A-B og B-A. 

A - B er elementene som de ikke er i B:

A - b = 6, 8

B - A er elementene i B som ikke er i A:

B - A = 1, 7, 9

Løste øvelser

Oppgave 1

Skriv symbolsk og også i forlengelse av kronbladet P for naturlige tall enda lavere enn 10.

Løsning: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Oppgave 2

Anta helheten til det som er dannet av de naturlige tallene som er faktorer på 210, og settet B som dannet av de naturlige tallene søskenbarn lavere enn 9. Bestem begge settene i forlengelsen og fastslå hvilket forhold det er mellom de to settene.

Løsning: For å bestemme elementene i sett A, må du begynne med å finne faktorene i det naturlige tallet 210:

210 = 2 * 3 * 5 * 7

Så er det skrevet en:

A = 2, 3, 5, 7

Vi fortsetter å vurdere Set B, som er søskenbarnene mindre enn 9. 1 er ikke fetter fordi den ikke oppfyller definisjonen av fetter: "et tall er fetter hvis og bare hvis det har nøyaktig to delere 1 og tallet i seg selv". The 2 er jevn og samtidig er fetter fordi den oppfyller definisjonen av fetter, de andre søskenbarnene mindre enn 9 er 3, 5 og 7. Så det sett B er:

B = 2, 3, 5, 7

Derfor er de to settene de samme: a = B.

Øvelse 3

Bestem settet hvis elementer x er forskjellig fra x.

Løsning: C = x / x ≠ x

Som ethvert element, antall eller objekt er lik seg selv, kan ikke C ikke være annet enn det tomme settet:

C = Ø

Oppgave 4

Være settet med n naturlige tall og z settet med hele tall. Bestem n ⋂ z y n ∪ z.

Løsning: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z fordi n ⊂ z.

Referanser

1. GARO, m. (2014). Matematikk: Kvadratiske ligninger: Hvordan løse en kvadratisk ligning. Marilù Garo.
2. Haeussler, e. F., & Paul, r. S. (2003). Matematikk for administrasjon og økonomi. Pearson Education.
3. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematikk 1 september. Terskel.
4. Dyrebar, c. T. (2005). Matematikkurs 3o. Redaksjonell progreso.
5. Matematikk 10 (2018). "Eksempler på endelige sett". Hentet fra: Matematikk10.nett
6. Wikipedia. Sett teori. Gjenopprettet fra: er.Wikipedia.com