Bernoulli teorem

Vi forklarer hva som er Bernoullis teorem, ligninger, applikasjoner og løser en øvelse

Hva er Bernoullis teorem?

Han Bernoulli teorem Han bekrefter at i en ideell væske som sirkulerer i en ledning, er den mekaniske energien per volumenhet av væsken konstant i alle seksjonene av røret, uavhengig av at de har forskjellige tverrseksjoner i området og høyden.

Nå er en ideell væske en som ikke kan komprimeres, så dens tetthet er fast, uavhengig av trykkverdien.

I tillegg har en ideell væske null viskositet, det vil si at det ikke er noen friksjon mellom væskelagene og verken mellom væsken og veggene i kanalen.

Betingelser med inkomprimerbarhet og nullviskositet er avgjørende for å anvende Bernoullis teorem. Det er også nødvendig at strømmen er stasjonær, det vil si at strømmen ikke varierer over tid.

På den annen side må strømmen være laminær, så det kan ikke være noen virvler eller turbulens under passering av kanalen.

Bernoulli ligning

Bernoulli -ligningen har tre begreper, arbeidet utført av presse P, kinetisk energi og gravitasjonspotensiell energi for hver volumetrisk tetthetsvæskeenhet ρ

Bernoullis ligning er:

På den annen side fastslår kontinuitetsligningen at strømmen i en ideell væske er konstant i alle deler av strømningsrøret. Det vil si at væskevolumet i samme tidsenhet er det samme i alle deler av røret.

Hvis strømmen er q, så:

Q = konstant

Med:

Q = a · v

Hvor a er tverrsnittsarealet til røret og v er hastigheten på væsken.

Kan tjene deg: kunstige satellitter

Det bemerkes at i de smaleste delene av røret må væsken sirkulere raskere, siden det forblir konstant, selv om den varierer. Derfor er kinetisk energi per volum av enhetene større.

Siden Bernoullis teorem slår fast at mekanisk energi er konstant i alle seksjoner, i de smalere delene av større kinetisk energi, reduseres potensiell energi. 

Den potensielle energien består av gravitasjonsenergi per volum av enhetene pluss arbeidet utført av trykket i et enhetsvolum, og ved å redusere den potensielle energien reduserer derfor også trykket.

Oppsummert resulterer den kombinerte effekten av prinsippet om kontinuitet og Bernoulli -teoremet i de smale delene av strømningsrøret, der væskehastigheten er større, trykket synker med hensyn til de bredere seksjonene.

Begrep i Bernoulli -ligningen

1) Arbeid utført av trykket per volum enhet 

I en del av tverrsnitt av området til, Væsken beveger en mengde s, På grunn av trykket p som produserer en kraft f = p⋅ a.

Arbeidet utført med makt er:

F⋅ s = p⋅ a⋅ s

Ettersom A⋅s -produktet representerer det fordrevne volumet, samsvarer arbeidet som er utført per enhetsvolum numerisk med verdien av P i seksjonen som er vurdert.

2) Kinetisk energi til et enhetsvolum av væske

Ettersom væsken er inkomprimerbar, har tettheten en fast verdi som kalles ρ.

Når væsken sirkulerer gjennom en seksjon av tverrsnitt A, og flytter en mengde s i en tid t, er strømningshastigheten:

Det kan tjene deg: Second Law of Thermodynamics: Formler, ligninger, eksempler

v = s/t

Og den kinetiske energien til nevnte væskedel er beregnet av:

K = ½ ρ (a⋅s) v²

Men hvis det fordrevne volumet (A⋅s) er enheten, vil begrepet kinetisk energi bli gitt av ½ ρ V².

3) Gravitasjonspotensiell energi på et enhetsvolum av væske i en høyde h 

For en deigvæskedel m og høyde h Når det gjelder et visst referansenivå, gis gravitasjonsenergi av:

U = m⋅ g⋅ h

Hvis deigen m Det tilsvarer en enhetlig væskedel ρ, Så den potensielle energien vil være ρemt g⋅ h.

Bernoulli teorem -applikasjoner

Aerodynamisk støtte

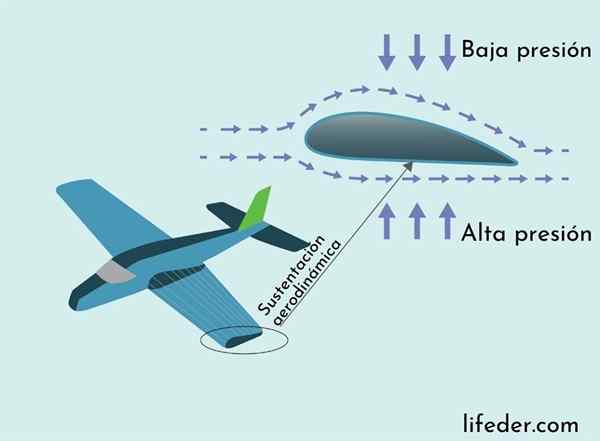Aerodynamisk støtte forklares av Bernoullis teorem

Kraften som forhindrer et fly fra fly til kollaps er den aerodynamiske støttekraften. Nettestøttekraften er rettet vertikalt opp og virker langs flyvingen. Opprinnelsen blir forklart gjennom Bernoullis teorem.

Vingen av et fly har et tverrsnitt med en lengre kurve øverst og kortere i bunnen. Dette gjør luftveien nær overflaten av vingen på toppen, så luften strømmer raskere over vingen enn bunnen. 

Som en konsekvens av Bernoullis teorem, er lufttrykket i den øvre delen av den sirkulerende vingen mindre enn nederst, noe sett i følgende bilde.

Det kan tjene deg: Fysikk under grekerne (Antige Hellas)

Lansering av baller og baller med kurveeffekt

I noen idretter som fotball, baseball og Cricke, vet erfarne spillere hvordan. Er det som kalles Effektlansering.

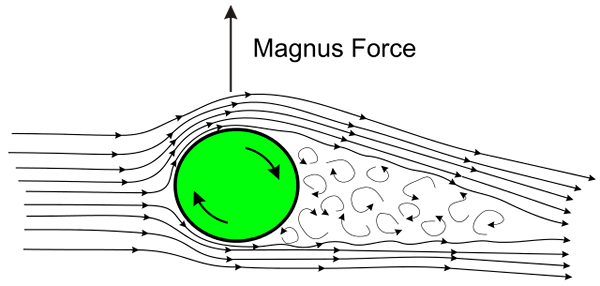Magnus effekt illustrasjon. Kilde: Wikimedia Commons

Effekten oppstår når ballen eller ballen svinger raskt mens du beveger seg gjennom luften. Rotasjonen forårsaker luften til overflaten av ballen blir dratt av den i to motsatte retninger, en til fordel for retning av oversettelsen og på den andre siden mot forskyvningsretningen.

Som et resultat av lufttrekken produseres et lavt trykkområde på et ansikt av ballen og på motsatt ansikt et høyt trykk, og produserer en nettokraft som avleder ballens naturlige bane.

Forklaringen på dette fenomenet kjent som Magnus -effekt Den ligger nettopp i Bernoullis teorem: der væsken sirkulerer raskt, er trykket lavt, og på siden der trykket sirkulerer sakte.

Trening løst

Et horisontalt rør har et område seksjon a₁ = 40 kvadratmeter₂ fire ganger lavere. Hvis vannstrømmen er 6 l/s, må du bestemme trykkforskjellen og høydeforskjellen i de vertikale rørene.

Løsning 

Starter fra strømningsligningen, hvis verdi er q = 6 l/s:

Q = a · v

Du må da hastigheten i den brede delen er 1,5 m/s og i den smale strekningen 6 m/s.

Deretter, påføring og matcher Bernoulli -ligningen på den brede og smale strekningen, oppnås en trykkforskjell på 1700 Pa, noe som tilsvarer en høydeforskjell i de vertikale rørene på 1,72 meter.