Euclid teorem

Hva er Euclids teorem?

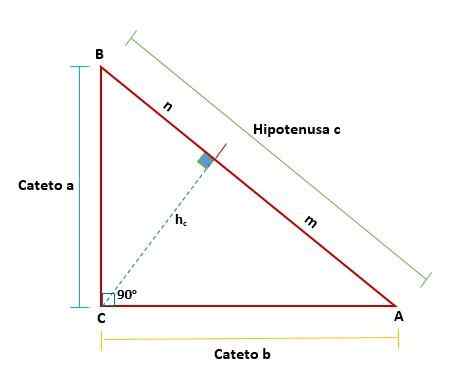
Han Euclid teorem Den demonstrerer egenskapene til en høyre trekant ved å tegne en linje som deler den inn i to nye rektangler som ligner hverandre og på sin side ligner den opprinnelige trekanten; Så det er et proporsjonalitetsforhold.

Euclides var en av de største matematikerne og geometre i alderdommen som gjorde flere demonstrasjoner av viktige teorier. En av de viktigste er den som bærer navnet hans, som har hatt en bred applikasjon.

Dette har vært slik fordi, gjennom det teoremet, forklarer de geometriske forholdene som eksisterer i rektangelet Triangle, der dette er relatert til deres anslag i hypotenusen.

Formler og demonstrasjon

Euclid teorem foreslår at i hver høyre trekant, når det er trukket en linje - som representerer på høyden som tilsvarer toppunktet i riktig vinkel med hensyn til hypotenus - er to rektangler dannet fra de originale trekantene fra originalen.

Disse trekantene vil være lik hverandre og vil også være lik den opprinnelige trekanten, noe som betyr at deres lignende sider er proporsjonale med hverandre:

Vinklene til de tre trekantene er kongruente; Det vil si når den roteres med 180 grader på toppunktet, sammenfaller en vinkel på den andre. Dette innebærer at alle vil være likeverdige.

På denne måten kan du også bekrefte likheten som eksisterer mellom de tre trekantene, for likestilling av dens vinkler. Siden likheten mellom trekanter, etablerer Euclid proporsjonene av disse fra to teorier:

• Høyde teorem.
• Katettingsteoremet.

Dette teoremet har en bred applikasjon. I eldgamle tider ble det brukt til å beregne høyder eller avstander, som representerer et stort fremskritt for trigonometri.

Kan tjene deg: beregning av tilnærminger ved bruk av differensialer

Det brukes for tiden på forskjellige områder som er basert på matematikk, for eksempel ingeniørfag, fysikk, kjemi og astronomi, blant mange andre områder.

Høyde teorem

Dette teoremet slår fast at høyden trekant i et hvilket.

Det vil si at kvadratet på høyden vil være lik multiplikasjonen av de projiserte bena som danner hypotenusen:

h_c² = m _* n

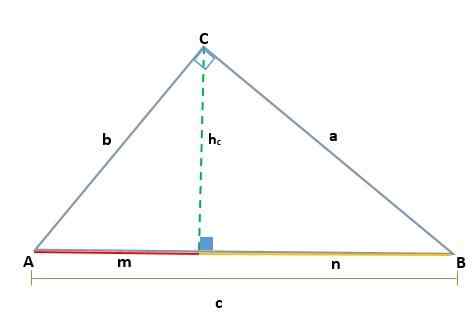
Demonstrasjon

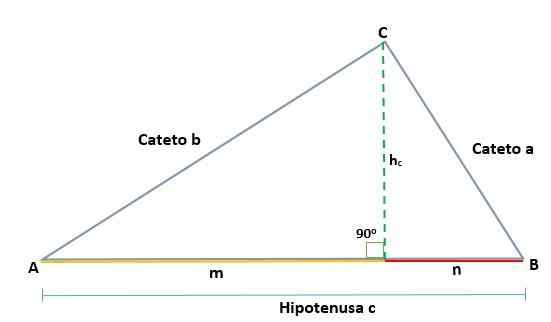
Gitt en ABC -trekant, som er rektangel i toppunkt C, genereres to lignende rektangler, ADC og BCD; Derfor er deres tilsvarende sider proporsjonale:

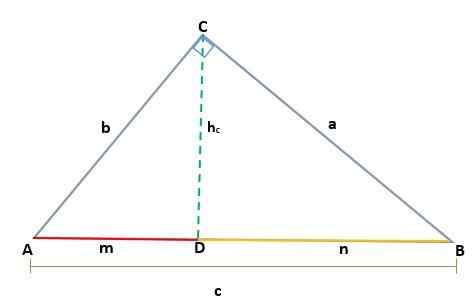
På en slik måte den høyden h_c Det tilsvarer CD -segmentet, tilsvarer Hypotenuse AB = C, så du må:

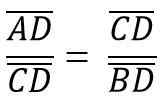
På sin side tilsvarer dette:

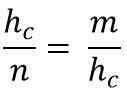
Rydde hypotenusen (h_c), For å multiplisere de to likestillingsmedlemmene, må du:

h_{C *} h_{C =} m _* n

h_c² = m _* n

Dermed blir verdien av hypotenusen gitt av:

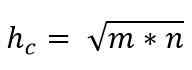
Katettingsteoremet

Dette teoremet slår fast at i hver høyre trekant vil målet for hver kateto være det geometriske proporsjonale gjennomsnittet (kvadratet for hver kateto) mellom målet på hypotenusen (komplett) og projeksjonen av hver og en på den:

b² = c _* m

til² = c_* n

Demonstrasjon

Gitt en ABC -trekant, som er rektangel i toppunkt C, slik at hypotenusa er C, når du tegner høyden (h) anslagene til kategoriene A og B er bestemt, som er henholdsvis segmentene M og N, og som er på Hypotenusen.

Dermed genererer høyden trukket på rektangelet Triangle ABC to lignende rektangler, ADC og BCD, slik at de tilsvarende sidene er proporsjonale, som dette:

Kan tjene deg: Hyperbolsk paraboloid: Definisjon, egenskaper og eksempler

Db = n, som er projeksjonen av CB -kateto på hypotenusen.

AD = M, som er projeksjonen av AC -kateto på hypotenusen.

Deretter bestemmes hypotenuse C av summen av bena i fremskrivningene:

C = m + n

På grunn av likheten mellom ADC og BCD -trekanter, må du:

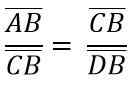
Ovennevnte er det samme som:

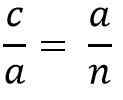
Å rydde "A" -kateto for å multiplisere de to likestillingsmedlemmene, må du:

til _* a = c _* n

til² = c _* n

Dermed blir verdien av kateto “a” gitt av:

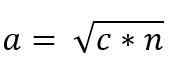
På samme måte, på grunn av likheten mellom ACB- og ADC -trekanter, må du:

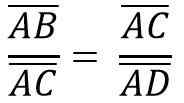
Ovennevnte er lik:

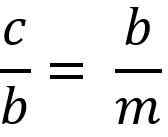
Å rydde "B" -kateto for å multiplisere de to likestillingsmedlemmene, må du:

b _* b = c _* m

b² = c _* m

Dermed blir verdien av kateto “B” gitt av:

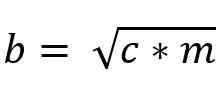
Forholdet mellom euklidteoremer

Teoremer med henvisning til høyden og kategoriene er relatert til hverandre fordi målet på begge er gjort med hensyn til hypotenusen til rektangelet Triangle.

Gjennom forholdet mellom euklidteoremer kan også høydenes verdi finnes; Det er mulig ved å fjerne verdiene til M og N av kategorien teorem og erstattes i høyde teorem. På denne måten blir det oppfylt at høyden er lik multiplikasjonen av bena, delt på hypotenusen:

b² = c _* m

m = b² ÷ c

til² = c _* n

n = a² ÷ c

I høyden er teorem m og n erstattet:

h_c² = m _* n

h_c² = (b² ÷ C) _* (til² ÷ C)

h_c = (b² _* til²) ÷ c

Løste øvelser

Eksempel 1

Gitt ABC -trekanten, rektangel i A, bestem målet på AC og AD, hvis AB = 30 cm og BD = 18 cm

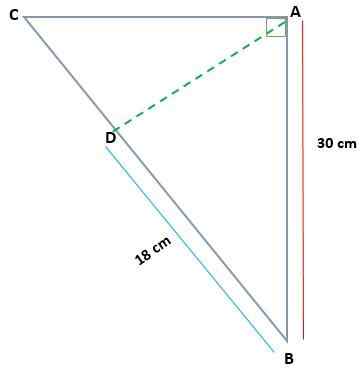
Løsning

I dette tilfellet er det tiltakene for et av de projiserte bena (BD) og en av tarkene til den originale trekanten (AB). På den måten kan du bruke kategori -teoremet for å finne verdien av BC -kateto.

Kan tjene deg: korrespondanse regel om en funksjon

AB² = BD _* BC

(30)² = 18 _* BC

900 = 18 _* BC

BC = 900 ÷ 18

BC = 50 cm

Verdien av CD -kateto kan bli funnet å vite at BC = 50:

CD = BC - BD

CD = 50 - 18 = 32 cm

Nå er det mulig å bestemme verdien av AC Cateto, anvende kategorien teorem igjen:

Ac² = CD _* Bd

Ac² = 32 _* femti

Ac² = 160

AC = √1600 = 40 cm

For å bestemme høydeverdien (AD), gjelder høyde teorem, siden verdiene til de projiserte kategoriene CD og BD er kjent:

Annonse² = 32 _* 18

Annonse² = 576

AD = √576

AD = 24 cm

Eksempel 2

Bestem verdien av høyden (h) til en MNL -trekant, rektangel i N, og kjenne til målene for segmentene:

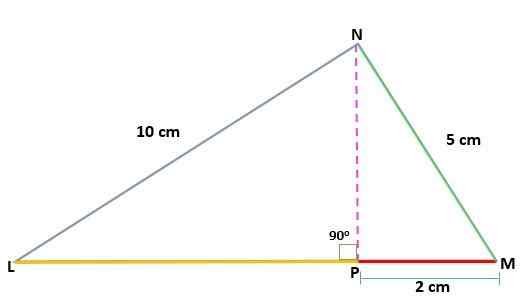
NL = 10 cm

Mn = 5 cm

PM = 2 cm

Løsning

Du har mål på et av de projiserte bena på Hypotenuse (PM), samt målene for de originale trekantkategoriene. På den måten kan du bruke kategori -teoremet for å finne verdien av den andre projiserte Cateto (LN):

Nl² = PM _* Lm

(10)² = 5 _* Lm

100 = 5 _* Lm

PL = 100 ÷ 5 = 20

Ettersom verdien av kategoriene og hypotenusen allerede er kjent, kan du gjennom forholdet mellom høyden og kategoriene bestemmes på høyden:

NL = 10

MN = 5

LM = 20

H = (b² _* til²) ÷ c.

H = (10² _* 5²)  ÷ (tjue)

H = (100 _* 25) ÷ (tjue)

H = 2500 ÷ tjue

H = 125 cm.