Steiner Forklaringsteorem, applikasjoner, øvelser

Han Steiner's teorem, også kjent som Parallell akse teorem, Det gjør det mulig å evaluere treghetsmomentet til et utvidet legeme, rundt en akse som er parallell med en annen som passerer gjennom objektets sentrum.

Det ble oppdaget av den sveitsiske matematikken_CM treghetens øyeblikk av objektet med hensyn til en akse som passerer gjennom CM og I massesenter_z treghetens øyeblikk med hensyn til en annen parallell akse til dette.

Figur 1. En rektangulær dør som slår på gleder har et øyeblikk av treghet som kan beregnes ved å bruke Steiner's teorem. Kilde: Pixabay.

Kjent avstanden D som skiller både akser og massen m fra den aktuelle kroppen, er treghetsmomentet med hensyn til inkognitoaksen:

Yo_z = Jeg_CM + MD²

Treghetsmomentet indikerer hvor enkelt det er for et objekt å rotere rundt en viss akse. Det avhenger ikke bare av kroppens kropp, men av hvordan den distribueres. Av denne grunn er det også kjent som Rotasjons treghet, Å være enhetene dine i det internasjonale KG -systemet . m².

Teoremet viser at treghetsmomentet Yo_z Det er alltid større enn treghetens øyeblikk Yo_CM i et beløp gitt av M.D².

[TOC]

applikasjoner

Ettersom et objekt er i stand til å rotere rundt mange akser, og i tabellene vanligvis bare treghetens øyeblikk angående aksen som passerer gjennom centroid, letter Steiner's teorem beregningen når den trenger å rotere kropper på aksler på aksler som ikke sammenfaller med dette.

Kan tjene deg: rettlinjet bevegelse: egenskaper, typer og eksempler

For eksempel dreier en dør ofte ikke om en akse som passerer gjennom massesenteret, men med hensyn til en sideakse, der hengslene fester seg.

Når du kjenner til treghetens øyeblikk, er det mulig å beregne den kinetiske energien forbundet med rotasjonen på denne aksen. Ja K er kinetisk energi, Yo treghetsmomentet rundt den aktuelle aksen og Ω Vinkelhastighet er oppfylt at:

K = ½ i.Ω²

Denne ligningen er veldig lik den veldig kjente formelen for kinetisk energi for et masseobjekt M beveger seg i hastighet v:  K = ½ m.v². Og er det treghetsmomentet eller rotasjons treghet Yo spiller i rotasjon den samme rollen som deigen M I oversettelsen.

Demonstrasjon av Steiner's teorem

Treghetsmomentet til et utvidet objekt er definert som:

I = ∫r² DM

Hvor DM Det er en uendelig masse masse og r Det er avstanden mellom DM og rotasjonsaksen z. I figur 2 krysser denne aksen midten av massen CM, men det kan være hvem som helst.

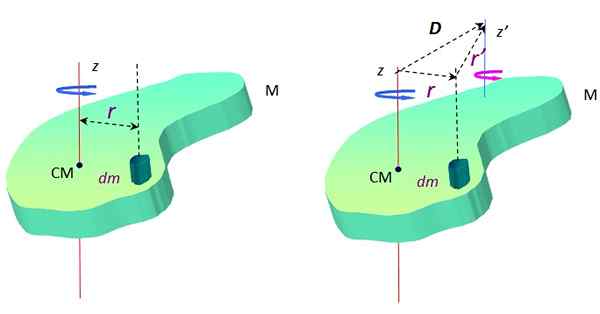Figur 2. Et objekt utvidet i rotasjon rundt to parallelle akser. Kilde: f. Zapata.

Rundt en annen akse  z ', Treghetsmomentet er:

Yo_z= ∫ (R ')² DM

Nå, i henhold til trekanten dannet av vektorene D, r og R ' (Se figur 2 til høyre), er det en vektorsum:

r + R ' = D   → R ' = D - r

De tre vektorene er på planet til objektet som kan være Xy. Opprinnelsen til koordinatsystemet (0,0) er valgt i CM for å lette beregningene som følger.

På denne måten kvadratmodulen til vektoren R ' er:

Kan tjene deg: Biofysikk: Historie, hvilke studier, applikasjoner, konsepter, metoder

(R ')² = (D_x- r_x)² +(D_og - r_og)² =

= D_x² + D_og² +r_x² + r_og2 -2d_xr_x - 2 d_ogr_og =

= D² + r²  - 2d_xr_x - 2 d_ogr_og

Nå erstattes denne utviklingen i integreringen av treghetsmomentet I_z og også definisjonen av tetthet DM = ρ brukes.DV:

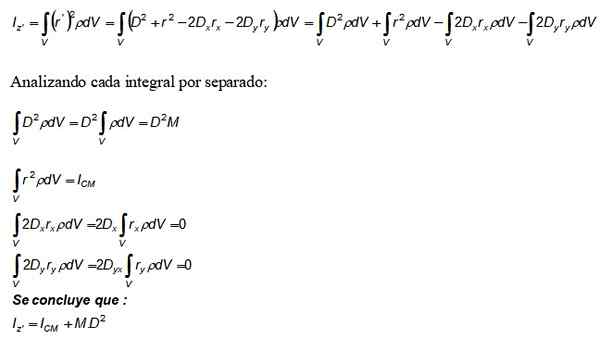
Begrepet m. D² Som vises i Steiner's teorem kommer fra det første integralen, det andre er treghetsmomentet angående aksen som går gjennom CM.

For sin del er de tredje og fjerde integraler verdt 0, siden de per definisjon utgjør CM -posisjonen, som er valgt som opprinnelsen til koordinatsystemet (0.0).

Løste øvelser

-Trening løst 1

Den rektangulære døren til figur 1 har en masse på 23 kg, 1,30 bred og 2,10 m høy. Bestem dørens treghetsøyeblikk angående aksen som går gjennom gleden, forutsatt at døren er tynn og ensartet.

Figur 3. Ordning for eksemplet løst 1. Kilde: Modified Pixabay.

Løsning

Fra et bord med treghetsmomenter, for en rektangulær plate av masse m og dimensjoner til og b, Treghetens øyeblikk med hensyn til aksen som passerer gjennom massesenteret er: i_CM = (1/12)M(til² + b²).

En homogen dør vil bli antatt (en tilnærming, siden døren til figuren sannsynligvis ikke er så mye). I dette tilfellet passerer massesenteret gjennom sitt geometriske sentrum. I figur 3 er det trukket en akse som passerer gjennom massesenteret, og som også er parallell med aksen som går gjennom gleden.

Yo_CM = (1/12) x 23 kg x (1.30²+2.10²) m² = 11.7 kg.m²

Kan tjene deg: Hva er en geoid?

Bruker Steiner's Teorem for den grønne rotasjonsaksen:

I = i_CM + MD² = 11.7 kg.m² + 23 kg x 0.652 m² = 21.4 kg.

-Trening løst 2

Finn treghetsmomentet til en tynn homogen stang når den dreier seg med hensyn til en akse som går gjennom en av dens ender, se figur. Er det større eller mindre enn treghetsmomentet når det dreier seg om sentrum? Fordi?

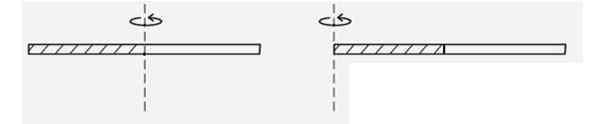Figur 4. Ordning for eksemplet løst 2. Kilde: f. Zapata.

Løsning

I henhold til treghetsmomentene, treghetens øyeblikk Yo_CM av en tynn stang av deig M og lengde L er: Yo_CM = (1/12) ML²

Og Steiner's teorem sier at når den roteres rundt en akse som går gjennom den ene enden d = l/2 gjenstår:

I = i_CM + MD² = (1/12) ML² + M (l/2)² = (1/3) ML²

Det er gammelt.

Påvirkningen av avstanden til rotasjonsaksen er ikke lineær, men kvadratisk. En masse som er det dobbelte av avstanden som en annen vil ha et øyeblikk av treghet proporsjonal med (2D)² = 4d².

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 313-340.
2. Georgia State University. Rotasjonsbevegelse. Gjenopprettet fra: Phys.Nthu.Edu.Tw.
3. Parallell akse teorem. Gjenopprettet fra: hyperfysikk.PHY-ASTR.GSU.Edu.
4. Rex, a. 2011. Fundamentals of Physics. Pearson. 190-200.
5. Wikipedia. Parallell akse teorem. Hentet fra: i.Wikipedia.org