Binomial teorem

Hva er binomial teorem?

Han Binomial teorem Det er en ligning som forteller oss hvordan et uttrykk for formen utvikler seg (a+b)ⁿ For noe naturlig tall n. En binomial er ikke annet enn summen av to elementer, for eksempel (a+b). Det lar oss også vite for et begrep gitt av^kb^N-K Hva er koeffisienten som følger med den.

Dette teoremet tilskrives ofte engelsk oppfinner, fysisk og matematiker Sir Isaac Newton; Imidlertid er det funnet forskjellige poster som indikerer at dens eksistens allerede var kjent i Midt -Østen, rundt året 1000.

Kombinatoriske tall

Den binomiale teoremen forteller matematisk følgende:

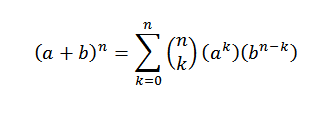
I dette uttrykket er a og b reelle tall og n er et naturlig tall.

La oss se noen grunnleggende konsepter som er nødvendige før vi gir demonstrasjonen.

Kombinatornummeret eller kombinasjonene av N i K er uttrykt som følger:

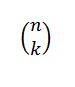
Dette uttrykker verdien av hvor mange undergrupper med K -elementer som kan velges fra et sett med N -elementer. Hans algebraiske uttrykk er gitt av:

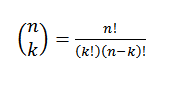
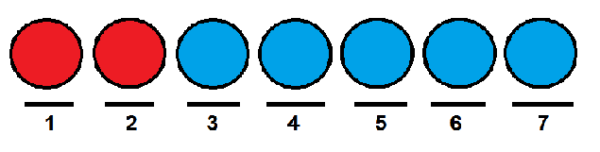
La oss se på et eksempel: Anta at vi har en gruppe på syv baller, hvorav to er røde og resten er blå.

Vi vil vite hvor mange måter vi kan bestille dem på rad. En måte kan være å plassere de to røde i første og andre plassering, og resten av ballene i posisjonene som gjenstår.

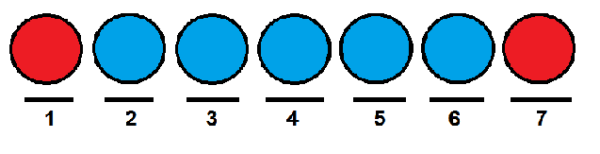
I likhet med forrige sak, kan vi gi de røde ballene henholdsvis den første og siste posisjonen, og okkupere de andre med blå baller.

Nå, en effektiv måte å telle hvor mange måter vi kan bestille ballene på rad bruker kombinatoriske tall. Vi kan se hver posisjon som et element i følgende sett:

Kan tjene deg: perfekte tall: hvordan identifisere dem og eksempler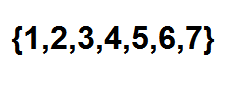

Nedenfor er bare å velge et undergruppe av to elementer, der hvert av disse elementene representerer posisjonen som de røde ballene vil okkupere. Vi kan gjøre dette valget i henhold til forholdet gitt av:

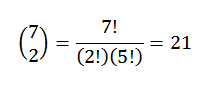
På denne måten har vi at det er 21 måter å bestille slike baller.

Den generelle ideen med dette eksemplet vil være veldig nyttig i demonstrasjonen av binomialteoremet. La oss se på et bestemt tilfelle: Hvis n = 4, har vi (A+B)⁴, Det er ikke noe mer enn:

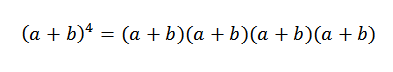
Når vi utvikler dette produktet, har vi summen av begrepene oppnådd ved å multiplisere et element av hver av de fire faktorene (A+B). Dermed vil vi ha vilkår som vil være i form:

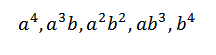
Hvis vi ønsket å skaffe skjemaets periode til⁴, Det er bare nok til å multiplisere som følger:

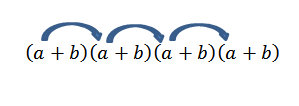
Merk at det bare er en måte å få dette elementet på; Men hva som skjer hvis vi nå ser etter slutten av skjemaet til²b²? Ettersom "A" og "B" er reelle tall, og derfor er det verdt kommutativ lov, vi må oppnå dette begrepet er å multiplisere med medlemmene som indikert av pilene.

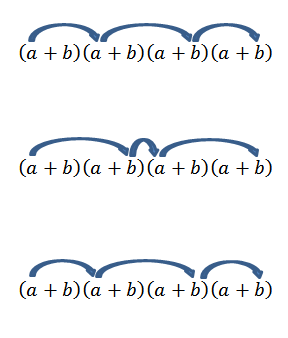
Å utføre alle disse operasjonene er vanligvis noe kjedelig, men hvis vi ser begrepet "A" som en kombinasjon der vi vil vite hvor mange måter vi kan velge to "A" fra et sett med fire faktorer, kan vi bruke ideen om Det forrige eksemplet på forrige eksempel. Så vi har følgende:

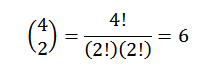
Dermed vet vi at i den endelige utviklingen av uttrykket (A+B)⁴ Vi vil ha nøyaktig 6²b². Ved å bruke den samme ideen til andre elementer, må du:

Kan tjene deg: transcendente tall: hva er, formler, eksempler, øvelser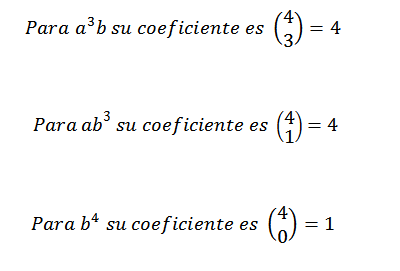

Så legger vi til uttrykkene som er oppnådd ovenfor, og vi må:

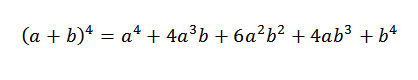
Det er en formell demonstrasjon for den generelle saken der "n" er noe naturlig tall.

Demonstrasjon

Merk at begrepene som er igjen når du utvikler (a+b)ⁿ De er fra skjemaet til^kb^N-K, hvor k = 0,1, ..., n. Ved å bruke ideen om det forrige eksemplet, har vi måten å velge "K" -variabler "A" av "N" -faktorene er:

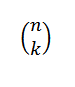
Når vi velger på denne måten, velger vi automatisk N-K-variabler "B". Dette følger det:

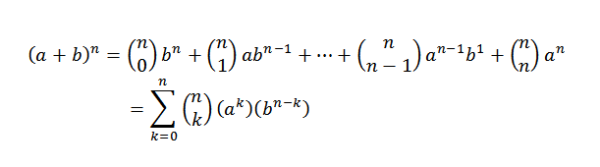
Eksempler

Vurderer (a+b)⁵, Hva ville være din utvikling?

For binomial teorem må vi:

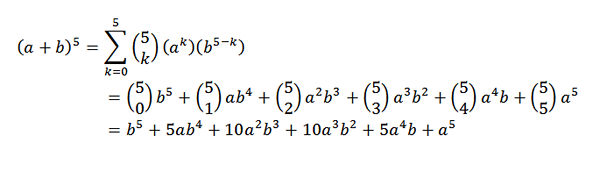
Binomial teorem er veldig nyttig hvis vi har et uttrykk der vi vil vite hva som er koeffisienten til et bestemt begrep uten å måtte utføre den komplette utviklingen. Som et eksempel kan vi ta følgende ukjent: Hva er X -koeffisienten⁷og⁹ I utviklingen av (x + y)¹⁶?

For binomial teorem har vi at koeffisienten er:

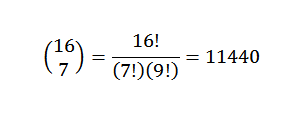
Et annet eksempel vil være: hva er X -koeffisienten⁵og⁸ I utviklingen av (3x-7y)^{1. 3}?

Først omskriver vi uttrykket på en praktisk måte; dette er:

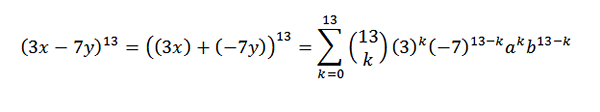
Deretter, ved å bruke binomial teorem, har vi at den etterspurte koeffisienten er når du har k = 5

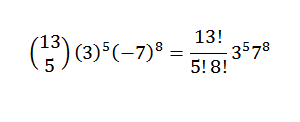
Et annet eksempel på bruken av dette teoremet er i demonstrasjonen av noen vanlige identiteter, for eksempel de vi vil nevne nedenfor.

Identitet 1

Hvis "n" er et naturlig tall, må vi:

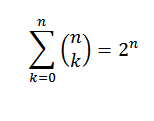
For demonstrasjonen bruker vi binomial teorem, der både "a" og "b" tar verdien av 1. Da har vi:

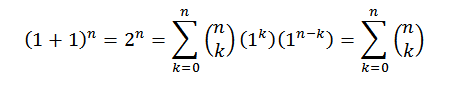
På denne måten har vi bevist den første identiteten.

Kan tjene deg: tilfeldige valg med eller uten erstatning

Identitet 2

Hvis "n" er et naturlig tall, så

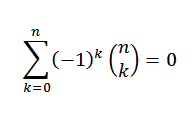
For binomial teorem må vi:

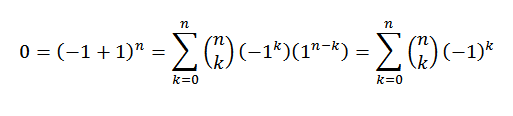
Nok en demonstrasjon

Vi kan gjøre en annen demonstrasjon for binomialteoremet ved å bruke den induktive metoden og identiteten til Pascal, som forteller oss at hvis "n" og "k" er positive heltall som oppfyller n ≥ k, så:

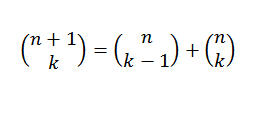
Induksjonsdemonstrasjon

La oss se at den induktive basen er oppfylt.  Hvis n = 1, må vi:

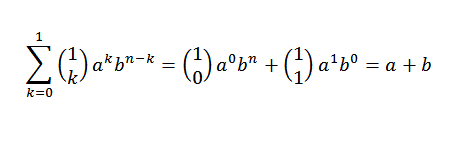
Vi ser faktisk at det er oppfylt. Nå, enten n = j slik at det er oppfylt:

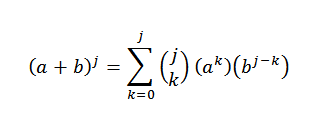
Vi vil se at for n = j+1 er det sant at:

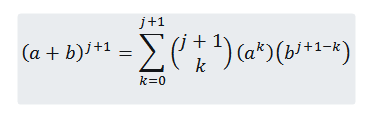
Så vi må:

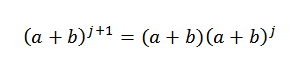
Ved hypotese vet vi at:

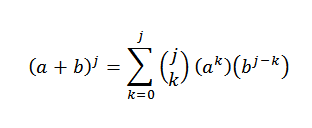
Deretter bruker Distributive Property:

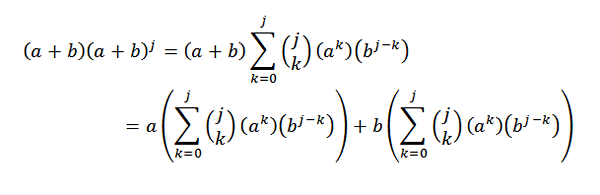
Deretter er det å utvikle hvert av sammendragene:

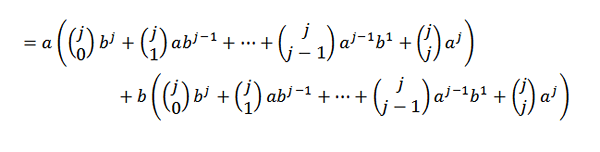
Hvis vi grupperer praktisk, må vi:

Ved å bruke Pascals identitet, må vi:

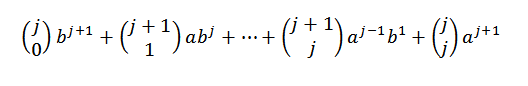
Til slutt, merk at:

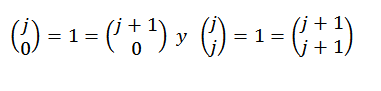
Derfor ser vi at den binomiale teorem er oppfylt for hvert "n" som tilhører naturlige tall, og med dette slutter testen.

Nysgjerrigheter

Kombinatornummeret (NK) kalles også binomial koeffisient fordi det nettopp er koeffisienten som vises i utviklingen av binomialen (A+B)ⁿ.

Isaac Newton ga en generalisering av dette teoremet for saken der eksponenten er et reelt tall; Dette teoremet er kjent som Newtons binomiale teorem.

Allerede i antikken var dette resultatet kjent for det spesielle tilfellet der n = 2. Denne saken er nevnt i Gjenstander av Euclid.