Typer integraler
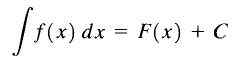
- 4532
- 161
- Jonathan Carlsen
De Typer integraler At vi er i beregningen er de ubestemte integralene og de definerte integralene. Selv om definerte integraler har mange flere applikasjoner enn ubestemte integraler, er det først nødvendig å lære å løse ubestemte integraler.
En av de mest attraktive anvendelsene av de definerte integralene er beregningen av volumet av et solid av revolusjon. Begge typer integraler har de samme linearitetsegenskapene, og også integrasjonsteknikkene er ikke avhengig av type integral.
Men til tross for at det er veldig likt, er det en hovedforskjell; I den første typen integral er resultatet en funksjon (som ikke er spesifikk), mens resultatet i den andre typen er et tall.
Grunnleggende typer integraler
Integralerens verden er veldig bred, men innen dette kan vi skille to grunnleggende typer integraler, som har stor anvendbarhet i hverdagen.
1- Ubestemte integraler
Hvis f '(x) = f (x) for alle x i domenet til f, sier vi at f (x) er et antiderivat, et primitivt eller et integrert av F (x).
På den annen side, la oss legge merke til at (f (x)+c) '= f' (x) = f (x), noe som innebærer at integralen til en funksjon ikke er unik, siden det å gi forskjellige verdier til konstanten C Vi vil skaffe forskjellige antiderivater.
Av denne grunn kalles f (x)+c det ubestemt integralet av f (x) og c kalles konstant av integrasjon, og vi skriver det som følger:
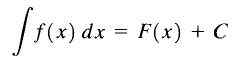 Ubestemt integral
Ubestemt integral Som vi kan se, er den ubestemte integralen til funksjonen f (x) en familie av funksjoner.
Hvis du for eksempel vil beregne det ubestemte integralet av funksjonen f (x) = 3x², må først et antiderivat av f (x) bli funnet først.
Kan tjene deg: trinomialDet er lett å merke seg at f (x) = x³ er et antiderivat, siden f '(x) = 3x². Derfor kan det konkluderes med at
∫f (x) dx = ∫3x²dx = x³+c.
2- definerte integraler
La y = f (x) En ekte funksjon fortsetter i et lukket intervall [a, b] og være f (x) et antiderivat av f (x). Det kalles det definerte integralet av F (x) mellom grensene A og B til tallet F (b) -F (a), og betegner som følger:
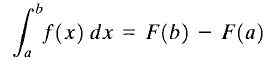 Grunnleggende beregningsteorem
Grunnleggende beregningsteorem Formelen vist ovenfor er bedre kjent som "den grunnleggende beregningsteoremet". Her "A" kalles nedre grense og "B" kalles øvre grense. Som det kan sees, er den bestemte integralen til en funksjon et tall.
I dette tilfellet, hvis det definerte integralet av F (x) = 3x² beregnes i intervallet [0,3], vil det oppnås et tall.
For å bestemme dette tallet velger vi f (x) = x³ som antiderivat av f (x) = 3x². Deretter beregner vi F (3) -F (0) som kaster oss som et resultat 27-0 = 27. Avslutningsvis er den definerte integralen av F (x) i intervallet [0,3] 27.
Det kan bemerkes at hvis g (x) = x³+3, så er g (x) valgt, er et antiderivat av f (x) forskjellig fra f (x), men dette påvirker ikke resultatet som g (3) -g (0) = (27+3)-(3) = 27. Av denne grunn vises ikke integrasjonskonstanten i de definerte integrasjonen.
En av de mest nyttige bruksområdene som denne typen integrer har, er at den gjør det mulig å beregne området (volumet) til en flat figur (av en solid revolusjon), og etablere tilstrekkelige integrasjonsfunksjoner og grenser (og en rotasjonsakse).
Blant de definerte integralene kan vi finne forskjellige utvidelser av denne som integrerte linjer, overflateintegraler, upassende integraler, flere integraler, alle med veldig nyttige applikasjoner innen vitenskap og ingeniørfag.
Det kan tjene deg: forskjell mellom sirkel og omkrets (med eksempler)Referanser
- Kishan, h. (2005). Integrert beregning. Atlantic Publisher & Distributors.
- Purcell, e. J., Varberg, d., & Rigdon, s. OG. (2007). Beregning (Niende utg.). Prentice Hall.

