Typer vinkler, egenskaper og eksempler

Det er mangfoldig Typer vinkler, Når de tar hensyn til flere kriterier for å differensiere dem, for eksempel kan de skilles gjennom sitt mål, etter den posisjonen de inntar og også i henhold til summen med andre vinkler.

Vanligvis er en vinkel definert som åpningen mellom to semi -rett med et vanlig opprinnelse, kalt toppunkt av vinkelen. De amplitude Åpning er målet på vinkelen, som ofte kommer i grader eller radianer.

En grad tilsvarer en av de 360 ​​delene der en omkrets kan deles. Hvis omkretsen er delt inn i to like deler, tilsvarer hver 180 grader eller 180º, hvis den i stedet er delt inn i fire like deler, vil hver være 90º og så videre. Dette systemet kalles Sexagesimal.

Radianes er et annet veldig brukt tiltak, som består av å ta en omkrets og måle vinkelen mellom to av radioene, hvis lengde er "R" og med toppunktet i midten av omkretsen. På denne måten blir buen "S" mellom disse radioene hevdet "R" også, og vinkelen underlagt da er 1 radián eller 1 rad og tilsvarer 57.3. grader.

Instrumentet for å måle vinkler er transportøren. For å ta et tiltak, falt sentrum av transportøren sammen med toppunktet i vinkelen og en av sidene på den samme med 0º -linjen til transportøren. Den andre siden sammenfaller med målet på vinkelen, som leses på skalaen.

Typer vinkler i henhold til ditt mål

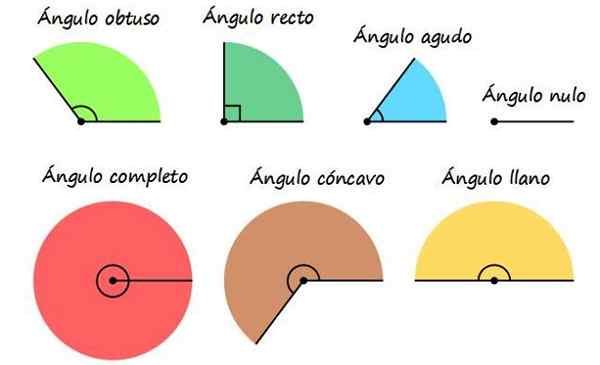
Klassifisering av vinkler etter deres mål. Kilde: Wikimedia Commons.

En av de hyppigste måtene å referere til vinkler på er å navngi dem i henhold til deres tiltak, selv om noen ganger kan en vinkel tilhøre mer enn en kategori beskrevet nedenfor.

Kan tjene deg: Variasjonskoeffisient: Hva er det for, beregning, eksempler, øvelser

Nullvinkel

Den hvis tiltak er 0º eller 0 rad, det vil si at de to semi -straks har en nullåpning.

Spiss vinkel

Målet på en akutt vinkel er mellom 0 og 90º eller mellom 0 og π/2 radianer. For eksempel er vinkler på 30º, 45º og 60º, som er en del av de bemerkelsesverdige vinklene, alle akutte vinkler.

Rett vinkel

Det er den som måler nøyaktig 90º (π/2 radianer), dette betyr at semistammene som definerer det er vinkelrett på hverandre.  De indre vinklene på et kvadrat eller et rektangel er rette vinkler, og det er også en rett vinkel som dannes mellom katetene til et rektangeletrekant.

Stump vinkel

Det er en vinkel større enn 90º eller π/2 radianer.

Flat vinkel

Den måler nøyaktig 180º, tilsvarer π -radianer. Når en vektorial størrelse er motsatt av en annen, danner de en vinkel på 180 º, for eksempel hastigheten på en mobil som beveger seg i en rett linje og retardasjonen oppleves når den blir stoppet.

Konveks vinkel

Hver gang en vinkel måler mindre enn 180º er en konveks vinkel. En akutt vinkel kan være konveks, som en av 90º og de stumpe vinklene hvis mål er inkludert i 90 º og 180º. Flere eksempler på konvekse vinkler er:

• 45º
• 60º
• 75º
• 135º

Konkav vinkel

Det er den som måler mer enn 180º, for eksempel 225º eller 270º, sistnevnte tilsvarer tre fjerdedeler av omkretsen.

Full eller perigonal vinkel

Tiltaket er 360º eller 2π radianer. Det betyr at de to semistammene som gjør det sammen, sammenfaller igjen, men i motsetning til nullvinkelen, har det i dette tilfellet vært en fullstendig sving.

Kan tjene deg: oval (geometrisk figur): egenskaper, eksempler, øvelser

Typer vinkler i henhold til sidens plassering

I mange figurer og geometriske strukturer vises mer enn en vinkel, og det er derfor det er praktisk å ha et kriterium for å sammenligne sidene av en med hensyn til en annen. På denne måten har de:

Påfølgende vinkler

De påfølgende vinklene er ved siden av hverandre, derfor har de en felles side og toppunkt.

Tilstøtende vinkler

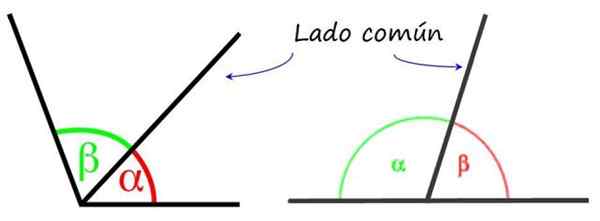Til venstre to vinkler på rad og til høyre to tilstøtende vinkler. Kilde: Wikimedia Commons/F. Zapata.

De tilstøtende vinklene har en felles side og toppunkt, det vil si at de presenterer seg ved siden av den andre. Men i motsetning til de påfølgende vinklene, er de tilstøtende sidene de resterende sidene motsatt semi -rett, derfor mellom de to vinklene totalt 180º.

Motsatte vinkler av toppunktet

De motsatte vinklene med toppunktet har toppunktet til felles, og sidene deres strekker seg overfor, fra en av vinklene til den andre. På denne måten har de motsatte vinklene med toppunktet samme tiltak.

Følgende figur viser 4 vinkler, betegnet med greske bokstaver. De blå vinklene er α og β, og som det kan sees, er de akutte og motsatte vinkler av toppunktet. På den annen side er vinklene γ og Δ stumpe vinkler og er også motarbeidet av toppunktet.

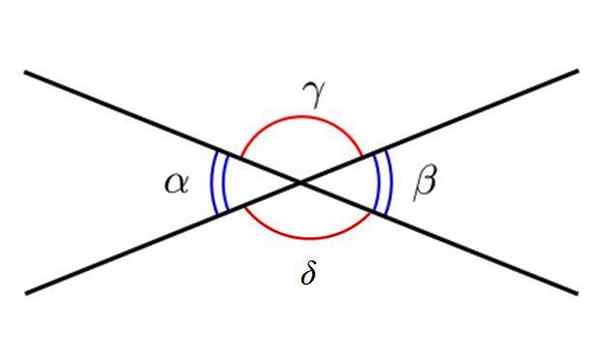Motsatte vinkler av toppunktet. Kilde: Wikimedia Commons.

Typer vinkler i henhold til summen av deres tiltak

Noen beregninger, spesielt i trigonometri, er veldig forenklet ved å observere om summen av målene for to vinkler er den av en av de bemerkelsesverdige vinklene, for eksempel riktig vinkel (90º) eller flatvinkelen (180º). I henhold til dette har de:

Komplementære vinkler

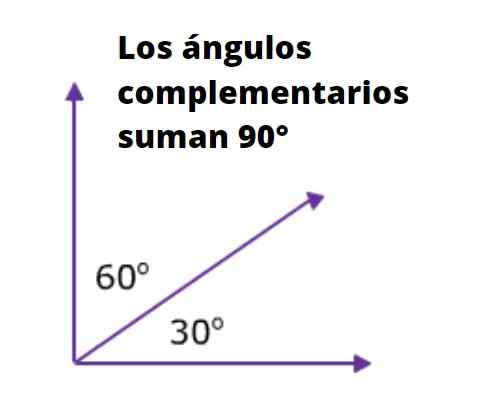
De vinklene hvis summen er lik 90º er komplementære. For eksempel er de indre akutte vinklene til et rektangel -trekant komplementære, siden summen av de tre indre vinklene er lik 180º.

Kan tjene deg: 90 Divisors: Hva er og forklaring

Siden en av de indre vinklene i rektangelet er måler 90º, er summen av de to andre også lik 90º.

Supplerende vinkler

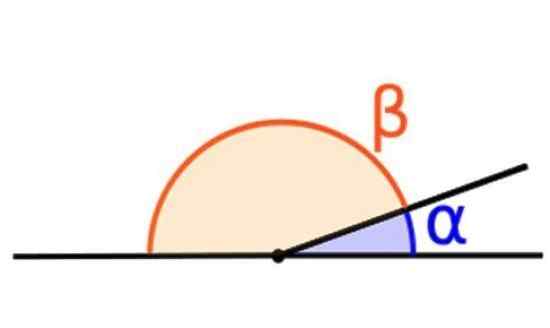Summen av to tilleggsvinkler er lik 180º. Kilde: Wikimedia Commons.

Er de vinklene hvis summen er lik 180º. For eksempel vinklene α og β vist i den øvre figuren.

Eksempler på bemerkelsesverdige vinkler som samtidig er supplerende er:

• 120º og 60º
• 135º og 45º

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Baldor. 1983. Flat og rom og trigonometri geometri. Kulturell hjemlandsgruppe.
3. OG. TIL. 2003. Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
4. Geometri 1st. Vinkler i omkretsen. Gjenopprettet fra: Edu.Xunta.er.
5. Rik, b. Geometri. 1991. Schaum -serien. 2. Utgave. McGraw Hill.