Parabolsk skuddegenskaper, formler og ligninger, eksempler

Han Parabolsk skudd Den består av å kaste et objekt eller et prosjektil med en viss vinkel og la den bevege seg under tyngdekraften. Hvis luftmotstand ikke blir vurdert, vil objektet, uavhengig av dens natur, følge en bane i form av en parabola.

Det er en daglig bevegelse, siden blant de mest populære idrettene er de som baller eller baller blir kastet, enten for hånd, med foten eller med et instrument som en racket eller et flaggermus for eksempel for eksempel.

Figur 1. Vannstrålen fra prydkilden følger en parabolsk bane. Kilde: Wikimedia Commons. Zátonyi Sandor (IFJ.), Fizped/CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)

For studier blir det parabolske skuddet delt opp i to overlappende bevegelser: den ene horisontale uten akselerasjon, og det andre vertikale med konstant akselerasjon ned, noe som er tyngdekraften. Begge bevegelsene har innledende hastighet.

La oss si at den horisontale bevegelsen tar. Hver av disse bevegelsene er uavhengig av den andre.

Med tanke på det faktum at å bestemme prosjektilposisjonen er hovedmålene, er det nødvendig å velge et passende referansesystem. Detaljene kommer neste.

[TOC]

Formler og ligninger av det parabolske skuddet

Anta at objektet blir kastet med vinkel α med hensyn til horisontal og innledende hastighet v_enten Som vist på figuren nedenfor til venstre. Det parabolske skuddet er en bevegelse som finner sted på flyet Xy Og i så fall dekomponerer den opprinnelige hastigheten som dette:

v_okse = v_enten cos α

v_Oy = v_enten sin α

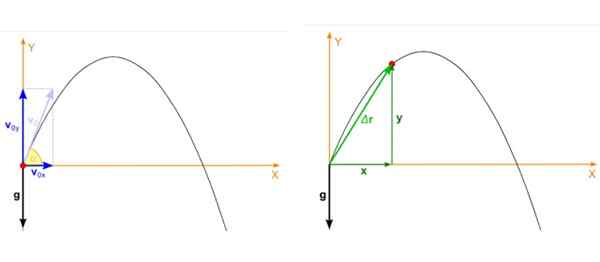Figur 2. Til venstre for den første hastigheten på prosjektilet og til høyre posisjon når som helst av lanseringen. Kilde: Wikimedia Commons. Zátonyi Sandor, (IFJ.) Fizped/CC By-SA (https: // creativeCommons.Org/lisenser/by-SA/3.0).

Prosjektilposisjonen, som er det røde punktet i figur 2, høyre bilde, har også to komponenter som er avhengige av tid, en i x Og den andre i og. Posisjonen er en vektor som er betegnet som r og enhetene er av lengde.

Kan tjene deg: Isomeria

I figuren sammenfaller den opprinnelige posisjonen til prosjektilet med opprinnelsen til koordinatsystemet, derfor x_enten = 0, og_enten = 0. Dette er ikke alltid tilfelle, opprinnelsen kan velges hvor som helst, men dette valget forenkler beregningene mye.

Når det gjelder de to bevegelsene i X og Y, er disse:

-X (t): Det er en jevn rettlinjet bevegelse.

-og (t): tilsvarer en jevn akselerert rettlinjet bevegelse med G = 9.8 m/s² og peker vertikalt ned.

I matematisk form:

x (t) = v_enten cos α.t

og (t) = v_enten .sin α.T - ½g.t²

Posisjonsvektoren gjenstår:

r (t) = [v_enten cos α.t]Yo + [v_enten .sin α.T - ½g.t²] J

I disse ligningene vil den imøtekommende leseren merke at minustegnet skyldes at alvorlighetsgraden peker på bakken, den følelsen som er valgt som negativ, mens den oppover blir tatt som positiv.

Siden hastighet er den første avledet fra stillingen, er det nok å utlede r (t) Når det gjelder tid og få:

v (t) = v_enten cos α Yo + (v_enten .sin α - Gt) J

Endelig uttrykkes akselerasjonen vektorisk som:

til (t) = -g J

- Bane, maksimal høyde, maksimal tid og horisontal rekkevidde

Bane

For å finne den eksplisitte ligningen av banen, som er kurven y (x), må du eliminere tidsparameteren, rydde i ligningen for x (t) og erstatte i y (t). Forenkling er noe arbeidskrevende, men det oppnås endelig:

Maksimal høyde

Maksimal høyde oppstår når v_og = 0. Å vite at det er neste forhold mellom posisjon og kvadratet med hastigheten:

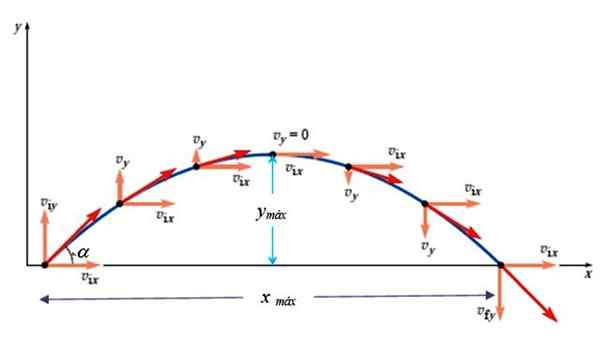Figur 3. Hastigheten i det parabolske skuddet. Kilde: Giambattista, a. Fysikk.

v_og² = v_Oy ²- 2gy

Driver med v_og = 0 Akkurat når den når i maksimal høyde:

0 = v_Oy ²- 2 g.og_Maks → Og_Maks = v_Oy ²/2 g

Med:

Kan tjene deg: Centripetal Acceleration: Definisjon, formler, beregning, øvelser

v_Oy = v_enten Sena

Maksimal tid

Maksimal tid er tiden som objektet tar for å nå og_Maks. For å beregne den brukes den:

v_og = v_enten .sin α - Gt

Vet det v_og Det er gjort 0 når t = t_Maks, resultat:

v_enten .sin α - g.t_Maks = 0

t_Maks = v_Oy /g

Maksimal horisontalt område og flytid

Omfanget er veldig viktig, fordi det indikerer hvor objektet vil falle. Så vi vil vite om det gir hvitt eller ikke. For å finne det trenger vi flytid, total tid eller t_v.

Av den forrige illustrasjonen er det lett å konkludere med det t_v = 2.t_Maks. Men oppmerksomheten er bare sant hvis lanseringen er på nivået, det vil si at høyden på utgangspunktet er den samme som høyden på ankomst. Ellers løser tiden den andre gradslikningen som følger av å erstatte den endelige posisjonen og_endelig:

og_endelig = v_enten .sin α.t_v - ½g.t_v²

I alle fall er det maksimale horisontale omfanget:

x_Maks = v_okse. t_v

Parabolsk skyteeksempler

Det parabolske skuddet er en del av bevegelsen av mennesker og dyr. Også av nesten alle idretter og spill der tyngdekraften griper inn. For eksempel:

Parabolsk skyting i menneskelige aktiviteter

-Steinen kastet av en katapult.

-Keeperens målspark.

-Ballen som kaster muggen.

-Pilen som kommer ut av buen.

-Alle slags hopp

-Kast en stein.

-Ethvert kastevåpen.

Figur 4. Steinen som kastes av katapulten og patey -ballen i finish -boksen er eksempler på parabolske skudd. Kilde: Wikimedia Commons.

Det parabolske skuddet i naturen

-Vannet spirer fra naturlige eller kunstige jetfly som en kilde.

-Steiner og lava spirer fra en vulkan.

-En ball som spretter på fortauet eller en stein som gjør det på vannet.

-Alle slags dyr som hopper: kenguruer, delfiner, gazeller, felines, frosker, kaniner eller insekter, for å nevne noen få.

Det kan tjene deg: Mekanisk kraft: Hva er, applikasjoner, eksemplerFigur 5. Impalaen er i stand til å hoppe opp til 3 m. Kilde: Wikimedia Commons. Arturo de Frias Marques/CC BY-S (https: // CreativeCommons.Org/lisenser/by-SA/3.0).

Trening

En gresshoppe som danner en vinkel på 55 º med horisontalt og lander ved 0.80 meter senere. Finne:

a) maksimal høyde nådd.

b) Hvis jeg hoppet med samme innledende hastighet, men dannet en vinkel på 45 º, ville den bli høyere?

c) Hva kan sies om maksimal horisontalt rekkevidde for denne vinkelen?

Løsning på

Når dataene som er gitt av problemet ikke inneholder den første hastigheten V_enten Beregningene er noe mer arbeidskrevende, men fra de kjente ligningene kan et nytt uttrykk trekkes. Starter fra:

x_Maks = v_okse . t_flygning = v_enten.cos α. t_v

Når den lander senere, er høyden 0 igjen, da:

v_enten .sin α.t_v - ½g.t_v²= 0

Som t_v Det er en vanlig faktor, den er forenklet:

v_enten .sin α - ½g.t_v= 0

Vi kan fjerne t_v Fra den første ligningen:

t_v = x_Maks / v_enten.cos α

Og erstatt i det andre:

v_enten .sin α - (½g.x_Maks / v_enten.cos α) = 0

Ved å multiplisere alle vilkår med v_enten.cos αUttrykket endres ikke og nevneren forsvinner:

(v_enten .sin α.) (v_enten.cos α) - ½g.x_Maks = 0

v_enten² sin α. cos α = ½g.x_Maks

Kan allerede ryddes v_enten eller også erstatte følgende identitet:

Sen 2α = 2 sen α. cos α → V_enten² Sen 2α = g.x_Maks

Beregnes v_enten²:

v_enten² = g.x_Maks / Sen 2α = (9.8 x 0.8 / sen 110) m²/s² = 8.34 m²/s²

Og til slutt maksimal høyde:

og_Maks= v_Oy ²/2g = (8.34 x sen² 55)/(2 x 9.8) M = 0.286 m = 28.6 cm

Løsning b

Hummeren klarer å opprettholde den samme horisontale hastigheten, men når vinkelen avtar:

og_Maks= v_Oy ²/2g = (8.34 x sen² 45)/(2 x 9.8) M = 0.213 m = 21.3 cm

Når en mindre høyde.

Løsning c

Det maksimale horisontale omfanget er:

x_Maks = v_enten² Sen 2a / g

Når vinkelen varierer, endres det horisontale omfanget også:

x_Maks = 8.3. 4 Sen 90 / 9.8  m = 0.851 m = 85.1 cm

Hoppet er lengre nå. Leseren kan bekrefte at det er maksimalt for vinkelen på 45 º da:

sin 2a = sin 90 = 1.

Referanser

1. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysikk. Andre utgave. McGraw Hill.
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fysisk. Vol. 1. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.