Vertikale skyteformler, ligninger, eksempler

Han vertikal skyting Det er en bevegelse som foregår under handling av et styrker, ofte tyngdekraften, og kan være stigende eller synke. Det er også kjent under navnet til Vertikal lansering.

Det mest umiddelbare eksemplet blir kastet opp (eller ned hvis du er foretrukket) en ball med hånden, ja, og sørg for å gjøre det vertikalt. Forakter luftmotstand, bevegelsen som følger ballen passer perfekt til den enhetlige varierte rettlinjede bevegelsesmodellen (MRUV).

Figur 1. Å snakke en ball vertikalt opp er et godt eksempel på vertikalt skudd. Kilde: Pexels.

Den vertikale skytingen er en mye studert bevegelse i de introduksjonskursene for fysikk, siden det er et utvalg av bevegelse i en dimensjon, En veldig enkel og nyttig modell.

Denne modellen kan ikke bare brukes til å studere kinematikken til objekter under virkning av tyngdekraften, men også, som vil bli sett senere, beskriver bevegelsen av partikler midt i et enhetlig elektrisk felt.

[TOC]

Formler og ligninger

Det første som trengs er et koordinatsystem for å indikere opprinnelsen og merke det med en bokstav, som i tilfelle av vertikale bevegelser er bokstaven "og"".

Da blir den positive sansen valgt +og, som vanligvis er oppe og mening -og som vanligvis er tatt ned (se figur 2). Alt dette med mindre hvem løser problemet bestemmer noe annet, siden et annet alternativ er å ta like positiv retning av bevegelsen, uansett hva dette er.

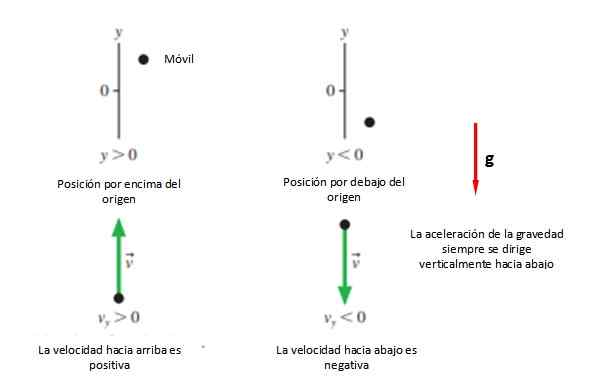Figur 2. Vanlige tegnkonvensjon i det vertikale skuddet. Kilde: f. Zapata.

I alle fall anbefales det at opprinnelsen sammenfaller med poenget med lanseringen og_enten, Fordi ligningene er forenklet, selv om enhver posisjon som er ønsket kan tas for å begynne å studere bevegelsen.

Det kan tjene deg: Andre likevektstilstand: Forklaring, eksempler, øvelser

Vertikale skytingslikninger

Når koordinatsystemet og opprinnelsen er etablert, går vi til ligningene. Størrelsene som beskriver bevegelsen er:

-Starthastighet v_enten

-Akselerasjon til

-Hastighet v

-Start posisjon x_enten

-Posisjon x

-Forskyvning Dx

-Tid t

Alle unntatt tid er vektorer, men siden det er en endimensjonal bevegelse med en viss retning, som betyr noe da bruker tegn på + eller - for å peke på hvor den aktuelle størrelsen er rettet. Når det gjelder vertikal skyting, går tyngdekraften alltid ned, og med mindre annet er spesifisert, tildeles et skilt -.

Det er da ligningene tilpasset den vertikale skytingen, og erstatter "x" av "og"Og"til" av "g"". I tillegg er tegnet (-) som tilsvarer tyngdekraften rettet:

1) Posisjon: y = y_enten + v_enten.T - ½ g.t²

2) hastighet: v = v_enten - g.t

3) Hastighet avhengig av forskyvningen Δog: v² = v_enten² - 2.g. Δog

Eksempler

Så er det applikasjonseksempler for vertikal skyting. I sin oppløsning må følgende tas i betraktning:

-""g”Det har en konstant verdi at i gjennomsnitt er 9,8 m/s² eller omtrent 10 m/s² Hvis det er foretrukket å lette beregninger når det ikke er for presisjon, er det nødvendig.

-Når v_enten Ok 0, Disse ligningene reduseres til de av fritt fall.

-Hvis lanseringen er oppe, må objektet ha en innledende hastighet som lar deg flytte. En gang i bevegelse når objektet en maksimal høyde som vil avhenge av hvor stor den opprinnelige hastigheten er. Selvfølgelig til større høyde vil mobilen bruke mer tid i luften.

-Objektet går tilbake til utgangspunktet med samme hastighet som det ble lansert, men hastigheten er rettet ned.

-For en vertikal lansering, jo høyere er den første hastigheten, jo raskere vil objektet komme til bakken. Her er avstanden som er tilbakelagt fast i henhold til den valgte høyden for lanseringen.

Kan tjene deg: det som er relativt og absolutt ruhet?

-I det vertikale skuddet beregnes tiden som tar mobilen for å nå den maksimale høyden ved å gjøre v = 0 I ligning 2) i forrige seksjon. Dette er maksimal tid t_Maks:

0 = v_enten - g . t_Maks ⇒ t_Maks = v_enten /g

-De maksimal høyde og_Maks Det er klar fra ligning 3) i forrige seksjon også å gjøre v = 0:

0 = v_enten² - 2.g. Δy ⇒ 0 = v_enten² - 2.g. (og_Maks - og_enten) ⇒ og_Maks = y_enten  + v_enten² / 2 g

Ja og_enten = 0, Det reduseres til:

og_Maks = v_enten² / 2 g

Løst eksempel 1

En ball med V blir kastet vertikalt oppover_enten = 14 m/s, fra toppen av en 18 m høy bygning. Ballen har lov til å følge nedstrøms til fortauet. Regne ut:

a) Maksimal høyde oppnådd av ballen med hensyn til bakken.

b) Tiden i luften (Flytid).

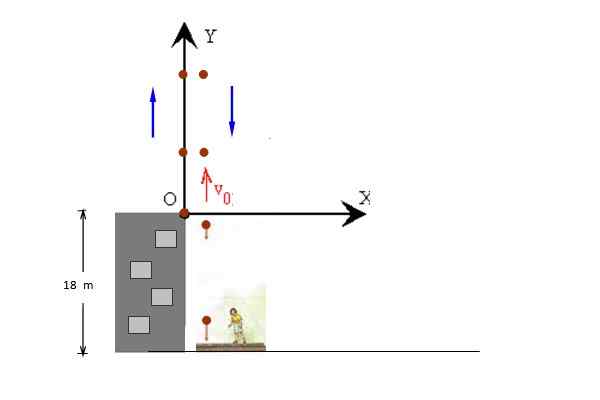Figur 3. En ball kastes vertikalt fra taket i en bygning. Kilde: f. Zapata.

Løsning

I figuren vises bevegelsene til stigende og senking av ballen separat for klarhet, men begge skjer på samme linje. Startposisjonen er tatt ved y = 0, slik at den endelige posisjonen er y = - 18 m.

a) Det maksimale målet målt fra taket på bygningen er og_Maks = v_enten² / 2 g Og fra uttalelsen leses det at den første hastigheten er +14 m/s, da:

og_Maks = (14 m/s)² / 2 x 9.8 m/s² = 10 m (Angående taket)

H_Maks = 10 m + 18 m = 28 m (Angående fortauet).

b) å finne Total tid enten Flytid som varer i luften. Ballen vil bli brukt ligningen y = y_enten + v_enten.T - ½ g.t², Med følgende verdier og tegn:

y = - 18 m

og_enten = 0 m

v_enten = +14 m/s

Erstatte:

- 18 = 14.T - ½ 9.8 .t²

- 4.9 t²+14.T + 18 = 0 

4.9 t²-14.T - 18 = 0

Det er en annen grads ligning som lett løses ved hjelp av en vitenskapelig kalkulator eller ved bruk av oppløsningen. Løsningene er: 3.82 og -0.96. Den negative løsningen blir kastet siden det er en tid mangler fysisk betydning.

Det kan tjene deg: Varme: Formler og enheter, egenskaper, hvordan det måles, eksempler

Flygingstiden for ballen er 3.82 sekunder.

Løst eksempel 2

En positivt lastet partikkel med Q = +1.2 Milicoulombs (MC) og masse m = 2.3 x 10 ^-10 Kg Det projiseres vertikalt opp, med start fra posisjonen vist på figuren og med innledende hastighet v_enten = 30 km/s.

Blant de lastede platene er det et elektrisk felt OG Uniform, rettet vertikalt ned og størrelsen på 780 N/C. Hvis avstanden mellom platene er 18 cm, vil partikkelen kollidere med den øvre platen? Forakte gravitasjonsattraksjonen på partikkelen, siden den er ekstremt lys.

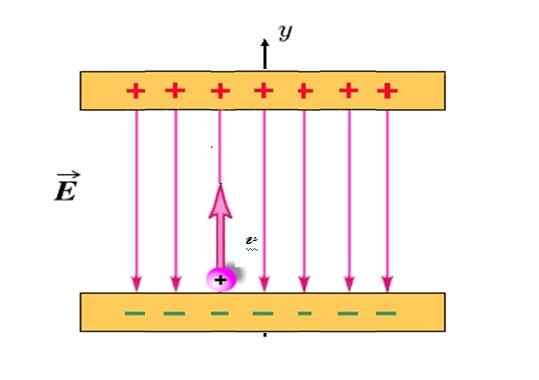Figur 4. En positiv belastningspartikkel beveger seg som en ball som kastes vertikalt oppover, når den er nedsenket i det elektriske feltet på figuren. Kilde: Modifisert av F. Wikimedia Commons sko.

Løsning

I dette problemet det elektriske feltet OG er den som produserer en styrke F og den påfølgende akselerasjonen. Partikkelen er alltid tiltrukket av den nedre platen, men når den blir projisert vertikalt oppover vil den når en positiv lastet, men når den blir projisert vertikalt oppover vil den nå en maksimal høyde og deretter gå tilbake til den nedre platen, for eksempel ballen i de forrige eksemplene.

Per definisjon av elektrisk felt:

E = f/q = m.A /q ⇒ a = q.E / m

Det er nødvendig å bruke denne ekvivalensen før du erstatter verdier:

1 MC = 1 x 10^-3 C

Med dette er akselerasjonen:

A = 1.2 x 10^-3 X 780 /2.3 x 10 ^-10m/s² = 4.07 x 10⁹ m/s²

For maksimal høyde brukes formelen til den foregående delen, men i stedet for å bruke "g"Denne akselerasjonsverdien brukes:

og_Maks = v_enten² / 2a = (30.000 m/s)²/2 x 4.07 x 10⁹ m/s² = 0.11 m = 11 cm

Ikke kolliderer med den øvre platen, siden den er 18 cm fra utgangspunktet, og partikkelen så snart den hever 11 cm.

https: // youtu.BE/KT08NTUDZWQ

Referanser

1. Kirkpatrick, l. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage Learning. 23 - 27.
2. Rex, a. 2011. Fundamentals of Physics. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14^th. Ed. Volum 1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9^na Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fysikk 10. Pearson Education. 133 - 149.