Toroid eller Toro Dona

Vi forklarer hva en okse eller okse er, dens egenskaper, volum, overflate, applikasjoner og viser flere eksempler

Hva er en toroid?

Han Toroid Det er en tre -dimensjonal geometrisk kropp i form av en bøyle, ring, ring, smultring eller smultring, derav navnet "Toro Dona", som tilhører klassen kalt objekter som heter Revolusjons faste stoffer.

En toroid genereres ved å rotere en lukket flat figur, rundt en linje som tilhører det samme planet på figuren, men avskjærer den ikke, som vist nedenfor:

En okse, som er en revolusjonsflate som oppnås ved å rotere en lukket flat figur (som en omkrets) rundt en fast akse. Kilde: Wikimedia Commons

Hovedkarakteristikken for toroiden er at til tross for at den er en lukket overflate, har den et hull. Dette betyr at to punkter på overflaten kan kobles sammen med et segment som er utenfor objektet.

Et annet kjennetegn ved toroiden er at det er en tredimensjonal figur uten toppunkter. Denne egenskapen deler den med andre volumetriske organer som sfæren, men mens sfæren er en konveks overflate, er oksen samtidig konkav og konveks.

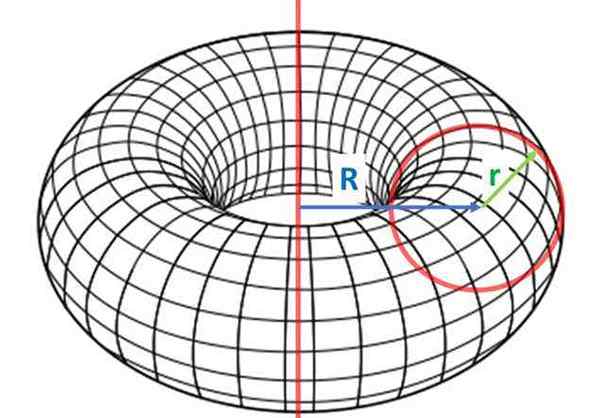
Blant oksene, oksen Det er det vanligste og oppnås fra rotasjonen av en radiokrets r, Angående en avstandsaks R av den første. Radio R (i små bokstaver) er kjent som mindre radius og R (kapital) er den største radius.

Volum av en toroid

En okse genereres ved å rotere en lukket flat figur av område TIL rundt en rotasjonsaks som ikke kutter den. Betegner av R Avstanden fra aksen til centroid av den flate figuren, volumet av Revolution Bull er:

Kan tjene deg: inverse trigonometriske funksjoner: verdi, derivater, eksempler, øvelser

V = 2πr⋅ a 

Dette resultatet oppnås når du bruker Pappus teorem For volumet av et faststoff av revolusjon, som sier at volumet av en fast revolusjon oppnås ved å multiplisere området til figuren som er brutt av omkretsen av omkretsen dannet ved rotasjon av centroid (eller tyngdepunkt ) av den roterte figuren, rundt rotasjonsaksen.

Volum av en okse

Oksen er toroidet som genereres av en radiokrets r. Hvis avstanden til rotasjonsaksen til midten av sirkelen roteres er r, er det da nødvendig å volum oksen er:

V = (2πr) ⋅ (πr²) = 2π²R³

Overflaten av en okse

Være en enkelt relatert flat figur TIL og kontur L. Hvis en slik figur roteres rundt en akse som er inneholdt i samme plan på figuren, men som ikke krysser den, er den genererte overflaten et område okse:

S = 2πr⋅ l

Å være avstanden fra aksen til tyngdepunktet eller centroid, av generatrix -figuren.

Dette resultatet er en konsekvens av Pappus teorem For overflaten av en faste revolusjon.

Overflaten av en okse

Det sirkulære krysset -avsnitts oksen av radio R (små bokstaver og radiorordfører R (store bokstaver) er en bestemt okse kalt Toro.

Som konturen av en radius r sirkel er 2πr, Da er området på overflaten til nevnte okse:

S = (2πr) ⋅ (2πr) = (4π²) (R⋅ r)

Toroid -applikasjoner

På grunn av sine geometriske egenskaper har oksen utallige praktiske og kulturelle applikasjoner. For å starte, er bøyler eller ringer toroidale deler som har forskjellige bruksområder:

Kan tjene deg: minimums torg

Kulturell

• Ornamental eller kosmetisk bruk når en ring plasseres på en finger, eller når en piercing er plassert i øret.
• I oksenes nese plasseres en bøyle, som tjener til å binde den og kontrollere den.
• Når ringen eller ringen er plassert i venstre hånd på ringfingeren, har den en sosial konnotasjon, som stammer fra de gamle grekerne, og betegner forpliktelse, troskap og ekteskap med paret som bærer en bøyle i samme måte og materiale.

I mekanikk

Utenfor ornamental, kosmetisk og kulturell kontekst har oksen mange praktiske bruksområder. I mekanikk brukes toroidet som en retensjonsring av lageret i kjøretøyets aksespiss. 

Lagrene på motorvogner er også sammensatt av en eller to bøyler i en okseform med forskjellige former for tverrsnitt, som de ruller sylindere eller kuler, med det formål å redusere friksjonen i aksene.

I strøm

I elektriske anvendelser er toroiden også av største betydning, siden de ferromagnetiske kjernene av induktorer, elektromagere og transformatorer ofte har en okseform og på seg en kabel i form av spole.

Tokamak

Det er en type kontrollert fusjonsreaktor i form av en toroid eller smultring kalt med det russiske navnet: tOkamak. I denne typen nukleær fusjonsreaktor har beholderen og spolene som produserer magnetfeltet til plasmatramming en toroidal form eller disposisjon.

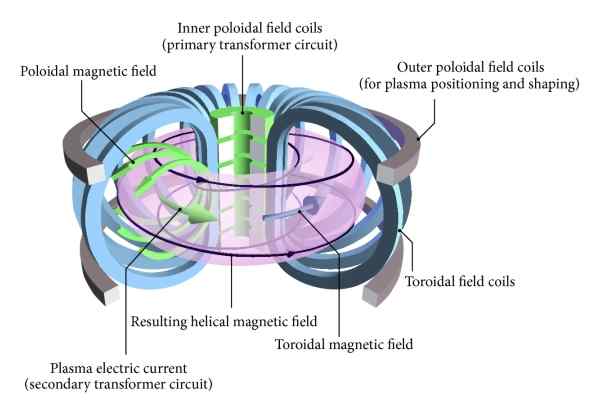Figuren viser skjematisk en kontrollert kjernefusjonsreaktor i en toroidal form som er kjent som "tokamak". I denne typen reaktor har både plasma, spoler og magnetfeltet for innesperring en toroidal konfigurasjon. Kilde: Wikimedia Commons

Eksempler

Overflaten til en firkantet seksjons okse (etter formel)

I dette eksemplet blir en firkantet seksjonsbull vurdert som vist i følgende figur:

Kan tjene deg: Scaleno Triangle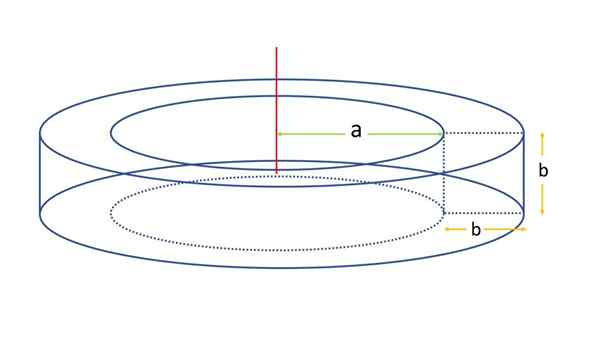 Firkantet seksjon toroid. Kilde: f. Zapata

Overflaten vil bli bestemt ved å bruke overflateformelen for en generell okse. For dette formål er det nødvendig å vite avstanden til rotasjonsaksen til centroid på torget, som ved bruk av den forrige nomenklaturen er R:

R = a + b/2

Det er også nødvendig å kjenne omkretsen L av Generatrix -figuren, som som i dette tilfellet er en firkant på siden b, Konturen vil være lang:

L = 4⋅B

Deretter brukes overflateformelen til en okse:

S = 2πr⋅l

Å erstatte R og L for deres tilsvarende uttrykk, avhengig av tiltak A og B for den firkantede oksen er:

S = 2π (a + b/2) ⋅4⋅b = 8π (a + b/2) ⋅b

Firkantet toroidoverflate (summen av ansiktene)

Den firkantede oksen til den forrige figuren består av fire ansikter: den øvre og den nedre er flate ringene, og interiøret og utsiden er sylindrisk.

Å ta hensyn til dette er det mulig å beregne overflaten ved å legge til området for de fire ansiktene.

Øvre og nedre ansikter har et område som tilsvarer den ytre sirkelen av radius (A+B) Mindre den av den indre sirkelen av radio til, som har som et resultat:

S_s= S_Yo= π [(a+b)² - b²] = π⋅ [a²+ 2ab]

Det indre sylindriske ansiktet har et område:

S₁= 2πab

Og det ytre sylindriske ansiktet har et område:

S₂= 2π (a+b) b = 2πab+2πb²

Slik at det totale arealet til toroid vil være summen s_s+S_Yo+S₁+S₂:

A = 2π⋅ [a²+ 2ab]+2πab+2πab+2πb².