Lineære transformasjonsegenskaper, hva er bruk, typer, eksempler

EN Lineær transformasjon, Som vi ganske enkelt vil kalle, relaterer elementene i to vektorrom V og W, og tilordner hver vektor v tilhører v en enkelt vektor W som tilhører W, gjennom en spesifikk operasjon.

Denne transformasjonen oppfyller to betingelser:

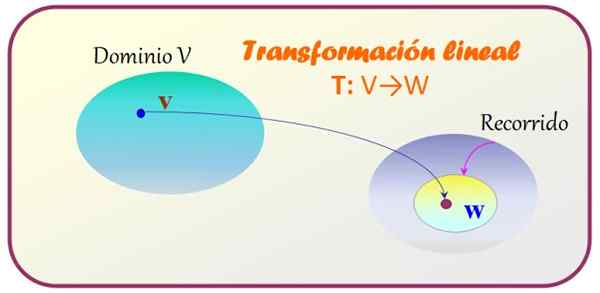
Figur 1. En lineær transformasjon gjelder en vektor av vektorrom v for å oppnå en annen vektor som tilhører W -vektorrommet. Kilde: f. Zapata.

-Tilstand 1

Det refererer til tillegget, slik at en t -lineær transformasjon må oppfylles det:

T (v + W) = T (v) + T (W)

-Tilstand 2

Den andre tilstanden representerer homogenitet i multiplikasjonen av en skalar med en vektor:

T (cv) = c⋅t (v)

Den lineære transformasjonen, som navnet tilsier, er ansvarlig for å kartlegge eller transformere elementer av V til elementer i w.

Notasjonen for funksjoner brukes også når det.

Et eksempel på lineær transformasjon er:

For å indikere at bokstaven t kommer til å bli brukt. Transformasjonen vil bli brukt på en vektor v hvis komponenter er x og y, som har blitt representert med en enkelt kolonnematrise. Resultatet er en annen vektor W hvis komponenter er x og 0, også representert med en kolonnematrise.

Derfor er dette en transformasjon av R -vektorrommet r² Mot vektorrommet r², at det i sammendrag er skrevet slik:

T: r² → R²         

Hvis vi har vektoren:

Transformasjonen returnerer oss:

Og så med hvilken som helst R -vektor². I eksempel 1 vil det bli bekreftet at denne transformasjonen er lineær.

[TOC]

Egenskaper for lineære transformasjoner

Anta at en lineær transformasjon av V i W, der vektorer v og eller De tilhører V, da blir følgende egenskaper oppfylt:

Eiendom 1

T (0) = 0

Hvor 0 er nullvektoren.

Eiendom 2

T (-v) = - t (v)

Eiendom 3

T (eller  - v) = T (eller) - T (v)

Eiendom 4

Være v = c₁v₁ + c₂v₂ +.. . +  c_nv_n

 Så:

T (c₁v₁ + c₂v₂ +.. . +  c_nv_n) = c₁ T (v₁) + c₂ T (v₂) +.. . +  c_n T (v_n)

Elementer av lineær transformasjon

La V og W allerede nevnte vektorrom der de lineære transformasjonene t transformerer elementer av V til w. Vi kan definere følgende elementer:

-C -kjernen eller kjernen: Det er en delmengde av domenet som det er betegnet av N (t) enten Ker (t) og forstå alle elementene i V slik at:

T (v) = 0.

Den lineære transformasjonen t (v) = 0 er kalt null transformasjon.

Naturligvis nullvektoren v = 0 oppfyller uansett med denne tilstanden, men kjernen består av hele ikke -null -vektorene som også oppfyller den, for en gitt t.

Kan tjene deg: Voksende funksjon: Hvordan identifisere den, eksempler, øvelser

-Bilde av t: Det er settet med vektorer som tilhører W slik som er bildet av minst noen vektor i V. Det er betegnet som Im t) Og det er undergruppen av W -vektorrommet.

Disse elementene vil hjelpe oss med å klassifisere lineære transformasjoner senere.

Hva er lineære transformasjoner for?

Opprinnelig fungerer lineære transformasjoner med vektorrom, dannet av vektorer. Mange ganger forbinder vi vektorer med styrke og andre fysiske størrelser, men i digital bildebehandling kan en piksel representeres av en vektor.

I så fall kan bildet manipuleres av praktiske lineære transformasjoner for å oppnå de ønskede effektene, for eksempel å projisere, rotere, finne speilbildet eller endre størrelsen uten å endre de relative dimensjonene.

Lineære transformasjoner er også mye brukt i økonomi og beslutningstaking, for eksempel for å vite mengden råstoff som kreves for å produsere et bestemt produktbatch.

Antall stykker som er nødvendige for å sette sammen de forskjellige modellene som er produsert av en fabrikk, kan arbeides gjennom en matrisearrangement, som vi vil se senere.

Typer lineære transformasjoner (klassifisering)

Som funksjoner kan lineære transformasjoner være:

-Injeksjon eller monomorfismer

-Bijektiver eller Epimorfismer

-Overbevis eller Isomorfismer

I tillegg er følgende typer:

-Endomorfismer

-Automorfismer.

Injiserende lineære transformasjoner

La V og W vektorrom og t en lineær transformasjon t: v → w. T er injeksjon når:

Ker (T) = 0

Lineære overvisningstransformasjoner

Hvis V og W er vektorområdene slik at T: V → W, sies det at T er bijektiv når:

Im (t) = w

Bijjektive lineære transformasjoner

En lineær transformasjon t: v → w er bijektiv når det er både injiserende og oversvivende. Derfor blir det oppfylt det:

Ker (T) = 0 og Im (t) = w

Endomorfismer

De er lineære transformasjoner der domene og codominium sammenfaller.

Automorfismer

Denne typen lineære transformasjoner er bijektive endomorfismer.

Spesielle lineære transformasjoner

Lineær operatør

En lineær transformasjon T: V → V, som går fra et vektorrom til samme vektorrom kalles Lineær operatør.

Null transformasjon

Null transformasjon er nevnt ovenfor, viktig for å finne kjernen til en lineær transformasjon:

Det kan tjene deg: tetradecágon

T: v → w slik at t (v) = 0 For alle v.

Identitetstransformasjon

T: v → v slik at t (v) = v  For alle v.

Transformasjon definert av en matrise

T: v → w slik at t (v) = Av, hvor a er en matrise og v Det er en kolonnevektor.

Lineal FUNTION

De lineære funksjonene til Y = MX -typen er lineære transformasjoner. Ta for eksempel y = 3x og se om den oppfyller de to forholdene i begynnelsen, og testet med to verdier A og B noen:

f (a+b) = 3 (a+b) = 3a+3b = f (a)+f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

Det er faktisk en lineær transformasjon.

applikasjoner

Lineære transformasjoner har matematiske applikasjoner, for eksempel:

-Koordinere aksler rotasjon.

-I løsningen av systemer med lineære differensialligninger.

-Selvverdi og autoveringsproblemer.

Og de har også applikasjoner innen andre vitenskapsfelt, for eksempel innen mekanikk, kvantemekanikk og økonomi, blant andre områder.

Eksempler på lineære transformasjoner

Eksempel 1

I mange mekanikkproblemer må vi finne projeksjonen av en vektor v tilhører rommet, på et visst fly. Denne vektoren v kan representere for eksempel en styrke.

Anta at du vil projisere vektoren v = På XY -flyet. Vi kan definere en lineær transformasjon gitt av følgende matrise:

Når vi bruker den på vektoren v Vi får en vektor hvis z -komponent blir kansellert. Geometrisk er det representert, med projeksjonen av v På XY -planet som den røde vektoren med to komponenter.

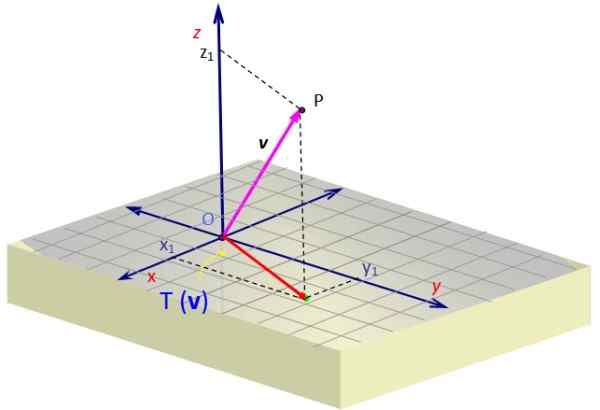Figur 2. Projeksjon av en vektor i rommet på et plan, som oppnås gjennom en lineær transformasjon. Kilde: f. Zapata.

Eksempel 2

Anta at du har en fabrikk som produserer tre typer leketøyvogner: C1, C2 og C3, som du igjen trenger tre typer stykker i visse mengder for å produsere hver type vogn:

-Akser eller stykke

-Hjul eller stykke B

-Chassis eller stykke c

For hver type vogn er antall stykker annerledes, siden modellene er forskjellige. Vi kan imøtekomme beløp.

Dette er et eksempel på transformasjon gitt av en matrise som ville være slik:

Hvis fabrikken mottar en viss innkjøpsordre, som består av x mengde C1, og  av C2 og z Fra C3, hvor mange stykker A, B og C må ha tilgjengelig for å sette sammen bestillingsvognene?

Det kan tjene deg: Hva er algebraiske uttrykk og som er de hyppigste?

Vi må finne en lineær transformasjon t (x) slik at:

Å få vektoren og:

Som vil gi oss mengden deler vi må ha til disposisjon. I året løst 2 evaluerer vi effektiviteten til de lineære transformasjonene for å finne mengden av deler som er nødvendige for å oppfylle en viss ordre.

Løste øvelser

- Oppgave 1

Sjekk at følgende transformasjon t: r² → R² Det er lineært:

Løsning

For å gjøre dette, må du sørge for at transformasjonen oppfyller de to forholdene som er beskrevet i begynnelsen, først tilsetningen og deretter produktet av en skalar for en vektor. Så du må ta to vektorer v og  eller tilhører r², Skrive dem etter matrise -notasjon eller spesifisere komponentene.

Disse vektorene er:

v = x₁, og₁

eller = x₂, og₂

Første tilstand

-Husker at vektorene er lagt til komponentkomponent, må det verifiseres at:

T (v+eller) = T (v) + T (eller)

T (v+eller) = T (x₁+ x₂ ; og₁ + og₂)

Herfra er det oppnådd at:

T (x₁+ x₂ ; og₁ + og₂) = (x₁+ x₂; 0)

-På den annen side, når du bruker transformasjonen på hver vektor hver for seg:

T (x₁,og₁) + T (x₂,og₂) = (x₁,0) + (x₂,0)

Ved å legge til de resulterende vektorene oppnås det effektivt:

W = (X₁+ x₂; 0)

Ettersom begge resultatene er identiske, er den første tilstanden fornøyd.

Andre tilstand

Nå skal vi bekrefte at ved å multiplisere med en scler C, kan den gå ut av transformasjonen:

T (cv) = c⋅t (v)

Sean:

v = x₁, og₁

c.v = C⋅x₁, C⋅y₁

Så:

T (cv) = T (c⋅x₁, C⋅y₁ ) = (C⋅x₁ , 0)

Men vi vet at fra forrige trinn at T (v) = T (x₁, og₁ ) = (X₁ , 0).

Så ettersom begge uttrykkene er identiske, blir den andre tilstanden også oppfylt og transformasjonen er lineær.

- Oppgave 2

En leketøyvognfabrikk samler tre kjøretøysmodeller: C1, C2 og C3, som du trenger stykker A, B og C som er henholdsvis aksler, hjul og chassis. De nødvendige beløpene er i følgende tabell:

Fabrikken har blitt bedt om å utarbeide 12 modeller C1, 22 C2 og 16 C3. Hvor mange stykker A, B og C er pålagt å fullføre bestillingen?

Løsning

Lineær transformasjon t (x) = y brukes, hvis resultat er produktet mellom matriser:

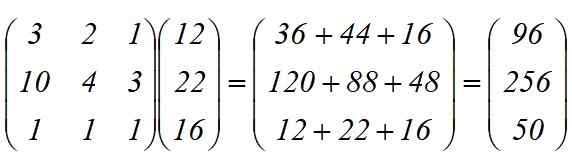
De er påkrevd totalt:

-96 akser

-256 hjul

-50 chassis.

Referanser

1. Algebra og analytisk geometri. Kjerne og bilde. Klassifisering av lineære transformasjoner. Gjenopprettet fra: AGA.frba.Utn.Edu.ar.
2. Grossman, s. 2012. Lineær algebra. 7. Utgave. McGraw Hill.
3. Gutiérrez, e. 2014. Lineær algebra og dens applikasjoner. Patria redaksjonell gruppe.
4. Larson, r. 2016. Grunnleggende om lineær algebra. 6. Utgave. Cengage Learning.
5. Wikipedia. Lineære applikasjoner. Gjenopprettet fra: er.Wikipedia.org.