Laplace Transform

Hva er Laplaces transformasjon?

De Laplace Transform Det har vært de siste årene av stor betydning innen ingeniørfag, matematikk, fysikk, blant andre vitenskapelige områder, siden det i tillegg til å være av stor interesse for det teoretiske, gir en enkel måte å løse differensialligninger, og transformere dem til algebraiske ligninger.

Opprinnelig ble Laplace Transform presentert av Pierre-Simon Laplace (1745-1827) i sin studie om teorien om sannsynlighet, og ble i prinsippet behandlet som et matematisk objekt av bare teoretisk interesse.

Nåværende applikasjoner oppstår når forskjellige matematikere prøvde å gi en formell begrunnelse til de "operasjonelle reglene" som ble brukt av Oliver Heaviside (1850-1925) i studiet av ligninger av elektromagnetisk teori.

Definisjon av Laplace -transformasjonen

La f være en definert funksjon for t ≥ 0. Laplace Transform er definert som følger:

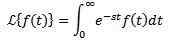
Det sies at Laplace -transformasjonen eksisterer hvis de tidligere integrerte konvergerer, ellers sies det at Laplace -transformasjonen ikke eksisterer.

Generelt sett, for å betegne funksjonen som er ønsket å transformere bittesmå bokstaver og store bokstaver tilsvarer transformasjonen. På denne måten vil vi ha:

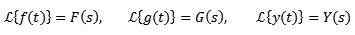
Eksempler

Vurder konstant funksjon f (t) = 1. Vi må transformere:

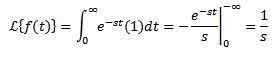
Forutsatt at integralen konvergerer, det vil si forutsatt at s> 0. Ellers, s < 0, la integral diverge.

La g (t) = t. Laplace -transformasjonen hans er gitt av:

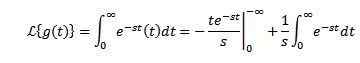
Når du integrerer av deler og vet det^-St Det har en tendens til 0 når T har en tendens til uendelig og s> 0, sammen med det forrige eksemplet vi må:

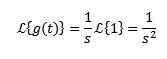
Transformasjonen kan eller ikke eksisterer, for eksempel for funksjonen f (t) = 1/t, integralen som definerer dens Laplace -transform.

Tilstrekkelige forhold for å sikre at Laplace -transformasjonen av en funksjon f eksisterer, er at F er kontinuerlig i deler for t ≥ 0 og er av eksponentiell rekkefølge.

Det sies at en funksjon er kontinuerlig i deler for t ≥ 0, når det for ethvert intervall [a, b] med en> 0, er det et begrenset antall punkter t_k, Hvor f har diskontinuiteter og er kontinuerlig i hvert underintervall [t_K-1,t_k].

På den annen side sies det at en eksponentiell funksjon C hvis det er reelle konstanter m> 0, C og T> 0 slik at:

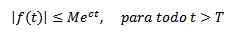
Som eksempler må vi f (t) = t² Det er eksponentielt, siden | t²| < e^3t For alle T> 0.

Formelt sett har vi følgende teorem:

Teorem (tilstrekkelige betingelser for eksistens)

Hvis f er en kontinuerlig funksjon for t> 0 og eksponentiell C, er det Laplace -transformasjonen for S> C.

Det er viktig å fremheve at dette er en tilstand av tilstrekkelighet, det vil si at det kan være en sak at det er en funksjon som ikke oppfyller disse forholdene, og likevel eksisterer Laplace -transformasjonen.

Et eksempel på dette er funksjonen f (t) = t^-1/2 som ikke er kontinuerlig i deler for t ≥ 0, men dens Laplace -transformasjon eksisterer.

Laplace -transformasjon av noen grunnleggende funksjoner

Følgende tabell viser Laplace -transformasjonene av de vanligste funksjonene.

Kan tjene deg: Hele tall

Historien om Laplace Transform

Laplace Transform skylder navnet Pierre-Simon Laplace, matematiker og fransk astronom og teoretiker som ble født i 1749 og døde i 1827. Hans berømmelse var slik at han var kjent som Newton i Frankrike.

I 1744 dedikerte Leonard Euler (1707-1783) studiene til integraler med skjemaet

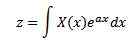
som løsninger av vanlige differensialligninger, men forlot raskt denne forskningen. Senere undersøkte Joseph Louis Lagrange (1736-1813), som beundret Euler mye, også denne typen integrerte og relaterte dem til teorien om sannsynlighet.

1782, Laplace

I 1782 begynte Laplace å studere disse integralene som løsninger på differensialligninger, og ifølge historikere bestemte han i 1785 seg for å omformulere problemet, som senere fødte Laplaces transformasjoner som de blir forstått i dag.

Etter å ha blitt introdusert innen sannsynlighetsteori, var det av liten interesse for forskere for øyeblikket, og ble bare sett på som et matematisk objekt bare av teoretisk interesse.

Heaviside Oliver

Det var i midten av nittende århundre da den engelske ingeniøren Oliver Heaviside oppdaget at differensialoperatører kan behandles som algebraiske variabler, og dermed ga sin moderne anvendelse til Laplace Transforms.

Oliver Heaviside var fysiker, engelsk elektrisk og matematisk ingeniør som ble født i 1850 i London og døde i 1925. Mens du prøvde å løse problemer med differensialligninger brukt på vibrasjonsteori, og ved bruk av Laplace -studier, begynte det å forme de moderne anvendelsene av Lapla -transformasjoner.

Resultatene eksponert av Heaviside spredte seg raskt.

Nytten av Heavisides arbeid når du løste fysikklikninger, fikk imidlertid at metodene deres var populære mellom fysikere og ingeniører.

Til tross for disse tilbakeslagene, og etter noen tiår med mislykkede forsøk, kan det på begynnelsen av 1900 -tallet gis en streng begrunnelse for de operasjonelle reglene som er etablert av Heaviside.

Disse forsøkene lønnet seg takket være innsatsen fra forskjellige matematikere, som Bromwich, Carson, Van der Pol, blant andre.

Laplace transformerer egenskaper

Blant egenskapene til Laplace -transformasjonen skiller følgende:

Linearitet

La C1 og C2 konstante og f (t) og g (t) funksjoner hvis transformasjoner av Laplace er henholdsvis f (s) og g (s), så må den:

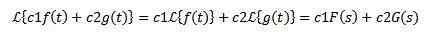
På grunn av denne egenskapen sies det at Laplace Transform er en lineær operatør.

Eksempel:

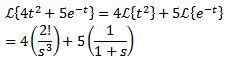
Første oversettelsessteorem

Hvis det skjer det:

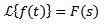
Og 'A' er noe reelt tall, da:

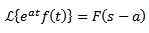
Eksempel:

Som Laplace de cos Transform (2T) = S/(S^2 + 4) Da:

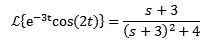
Andre oversettelsessteorem

Ja

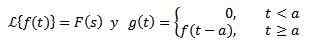
Så

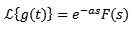
Eksempel:

Hvis f (t) = t^3, så f (s) = 6/s^4. Og derfor transformasjonen av 

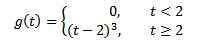
er g (s) = 6e^-2s/s^4

Endring av skala

Ja

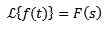
Og 'A' er virkelig annerledes enn null, må vi

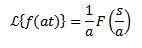
Eksempel:

Som transformasjonen av f (t) = sen (t) er f (s) = 1/(s^2 + 1)

Kan tjene deg: utviklet notasjon: Hva er eksempler og øvelser

Laplace forvandlet fra derivater

Hvis f, f ', f ", ..., f^(N) De er kontinuerlige for t ≥ 0 og er eksponentielle og f^(N)(t) er kontinuerlig i deler for t ≥ 0, deretter

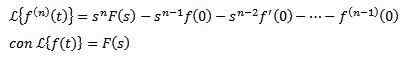
Integrert Laplace -transformasjon

Ja

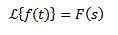
Så

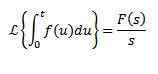
Multiplikasjon med tⁿ

Hvis vi må

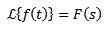
Så

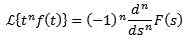
Divisjon av t

Hvis vi må

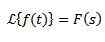
Så

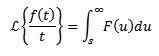
Periodiske funksjoner

La f være en periodisk funksjon med periode t> 0, det vil si f (t +t) = f (t), deretter

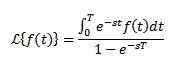
Oppførsel av f (s) når s har en tendens til uendelig

Hvis f er kontinuerlig i deler og av eksponentiell rekkefølge og

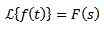
Så

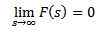
Inverse transformert

Når vi bruker Laplace -transformasjonen til en funksjon f (t), oppnår vi f (s), som representerer nevnte transformasjon. På samme måte kan vi si at f (t) er transformasjonen av det inverse laplace av f (s), og er skrevet som

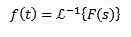
Vi vet at Laplace -transformasjonene til f (t) = 1 og g (t) = t er f (s) = 1/s og g (s) = 1/s² henholdsvis, derfor må vi

Noen vanlige Laplace -transformerte er følgende

I tillegg er den omvendte Laplace -transformasjonen lineær, det vil si at det er oppfylt det

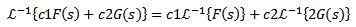
Trening

Finne

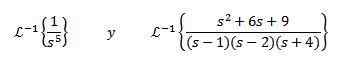
For å løse denne øvelsen må vi samsvare med F (S) -funksjonen med noen av forrige tabell. I dette tilfellet, hvis vi tar n + 1 = 5 og bruker linearitetsegenskapen til omvendt transformasjon, multipliserer vi og deler med 4! Får

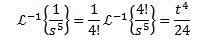
For den andre omvendte transformasjonen bruker vi delvise brøk for å omskrive funksjonen f (s) og deretter linearitetens egenskap, og oppnå

Som vi kan se av disse eksemplene, er det vanlig at funksjonen f (s) som er evaluert ikke stemmer overens med nettopp noen av funksjonene som er gitt i tabellen. For disse tilfellene, som observert, er det nok å omskrive funksjonen til den når riktig form.

Laplace Transform Applications

Differensiallikninger

Hovedprogrammet som Laplace transformerer har er å løse differensialligninger.

Ved å bruke egenskapen til transformasjonen av et derivat er det klart at

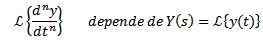
Og av n-1 avledet evaluert ved t = 0.

Denne egenskapen gjør den transformerte.

Følgende eksempler viser hvordan du bruker Laplace -transformasjonen for å løse differensialligninger.

Eksempel 1

Gitt følgende initialverdiproblem

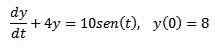
Bruk Laplace -transformasjonen for å finne løsningen.

Vi bruker Laplace -transformasjonen til hvert medlem av differensialligningen

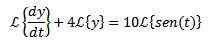
For eiendommen til transformasjonen av et derivat vi har

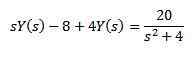
Når vi utvikler alt uttrykket og ryddingen og (e) har vi

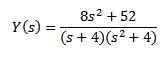
Bruke delvis brøk for å omskrive høyre side av ligningen vi oppnår

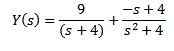
Til slutt er målet vårt å finne en funksjon og (t) som tilfredsstiller differensialligningen. Bruke det inverse Laplace -transformasjonen det resulterer i

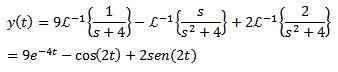
Eksempel 2

Løse

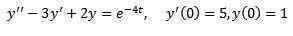
Som i forrige tilfelle, bruker vi transformert på begge sider av ligningen og separat terminperiode.

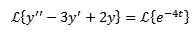
På denne måten har vi som et resultat

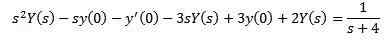
Erstatning med de opprinnelige verdiene som er gitt og rydding og (er)

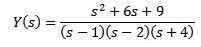
Ved å bruke enkle brøk kan vi omskrive hvordan ligningen følger

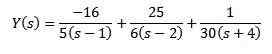
Og å bruke omvendt transformasjon av Laplace gir oss som et resultat

I disse eksemplene kan feil konklusjon oppnås at denne metoden ikke er mye bedre enn tradisjonelle metoder for å løse differensialligninger.

Kan tjene deg: proporsjon

Fordelene som tilbys av Laplace -transformasjonen er at det ikke er nødvendig.

I tillegg, når vi løser innledende verdiproblemer med denne metoden, bruker vi fra begynnelsen av de første forholdene, så det er ikke nødvendig å utføre andre beregninger for å finne den spesielle løsningen.

Differensialligningssystemer

Laplace Transform kan også brukes til å finne løsninger på samtidig vanlige differensialligninger, som vist i følgende eksempel.

Eksempel

Løse

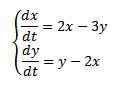
Med de opprinnelige forholdene x (0) = 8 e y (0) = 3.

Hvis vi må

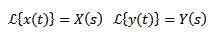
Så

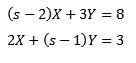
Løsning gir oss som et resultat

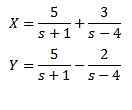
Og når vi bruker omvendt transformasjon av Laplace har vi

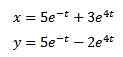
Mekanikk og elektriske kretsløp

Laplace Transform er av stor betydning i fysikken, har hovedsakelig applikasjoner for mekanikk og elektriske kretsløp.

En enkel elektrisk krets er sammensatt av følgende elementer:

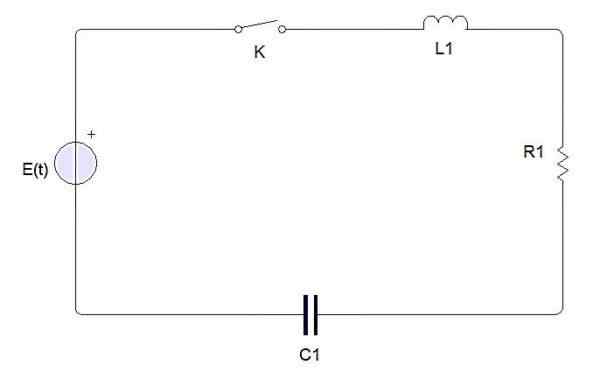Elementer i en elektrisk krets

En bryter, et batteri eller kilde, en induktor, en motstand og en kondensator. Når bryteren er lukket en elektrisk strøm som er betegnet av I (t). Kondensatorbelastningen er betegnet med Q (t).

Av Kirchhoffs andre lov, må spenningen produsert av fuente e til den lukkede kretsen være lik summen av hver av spenningsfastene.

Elektrisk strøm I (t) er relatert til belastning q (t) i kondensatoren gjennom i = dq/dt. På den annen side er spenningsfallet i hvert av elementene definert som følger:

Spenningsfallet i en motstand er IR = R (DQ/DT)

Spenningsfallet i en induktor er l (di/dt) = l (d²Q/dt²)

Spenningsfallet i en kondensator er Q/C

Med disse dataene, og anvendelse av Kirchhoffs andre lov på den enkle enkle kretsen, oppnås en annen -ordre differensialligning som beskriver systemet og lar oss bestemme verdien av Q (t).

Eksempel

En induktor, en kondensator og motstand er koblet til et batteri E, som vist på figuren. Induktoren er 2 Henries, 0,02 Farads -kondensatoren og 16 Onhmios -motstanden. For øyeblikket t = 0 lukker kretsen. Finn belastningen og strømmen når som helst t> 0 hvis e = 300 volt.

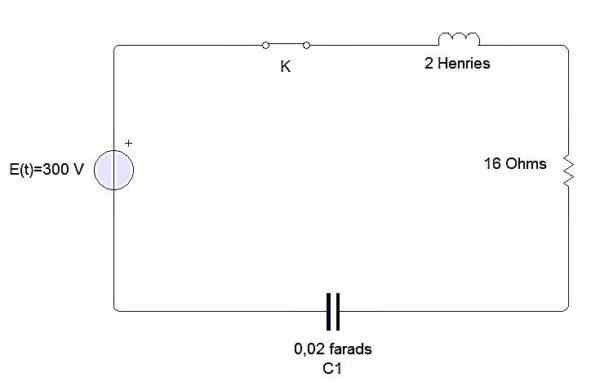
Vi har at differensialligningen som beskriver denne kretsen er som følger:

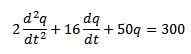
Der de opprinnelige forholdene er q (0) = 0, i (0) = 0 = q '(0).

Bruke Laplace -transformasjonen vi får det

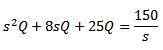
Og rydding Q (t)

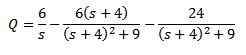
Deretter bruker vi den inverse Laplace -transformasjonen vi har

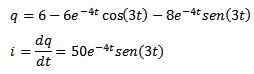
Referanser

1. G.Holbrook, J. (1987). Laplace Transform for Electronics Engineers. Limusa.
2. Ruiz, l. M., & Hernandez, m. P. (2006). Differensielle og transformerte ligninger av Laplace med applikasjoner. UPV -redaksjon.
3. Simmons, g. F. (1993). Differensialligninger med historiske applikasjoner og notater. McGraw-Hill.
4. Spiegel, m. R. (1991). Laplace forvandlet. McGraw-Hill.
5. Zill, d. G., & Cullen, m. R. (2008). Differensialligninger med verdier av verdipapirer i grensen. Cengage Learning Editores, S.TIL.