Fourier diskrete transformerte egenskaper, applikasjoner, eksempler

De Fourier diskret transformert Det er en numerisk metode som brukes til å definere prøver relatert til spektralfrekvensene som utgjør et signal. Studerer periodiske funksjoner i lukkede parametere, og kaster som et resultat et annet diskret signal.

For å få den diskrete transformasjonen av Furier fra N -punkter, på et diskret signal, må følgende to forhold på en sekvens være oppfylt X [n]

 x [n] = 0   N n - 1

Oppfyller disse forholdene, Fouriers diskrete transformasjon kan defineres som

Tdf

Fouriers diskrete transform.

[TOC]

Tolkning av Fouriers diskrete transformasjon

Kilde: Pexels

Det er 2 synspunkt som resultatene oppnådd fra en sekvens x kan tolkes_s[n] gjennom Fouriers diskrete transformasjon.

-Den første tilsvarer de spektrale koeffisientene, allerede kjent for Fourier -serien. Det observeres i diskrete periodiske signaler, med prøver sammenfallende med sekvens x_s[N].

-Det andre handler om spekteret av et diskret aperiadisk signal, med prøver som tilsvarer sekvens x_s[N].

Den diskrete transformasjonen er en tilnærming til spekteret av det opprinnelige analoge signalet. Fasen avhenger av prøvetakingsøyeblikk, mens størrelsen avhenger av prøvetakingsintervallet.

Egenskaper

Algebraiske grunnlag av struktur utgjør det logiske grunnlaget for følgende seksjoner.

Linearitet

C . S_n → c . F [S_k]; Hvis en sekvens multipliseres med en skalar, vil transformasjonen også være.

T_n + V_n = F [t_k]+F [v_k]; Transformasjonen av en sum er lik summen av de transformerte.

Dualitet

F [s_n] → (1/n) s_-K; Hvis den diskrete transformasjonen av Fourier huskes til et uttrykk som allerede er transformert, oppnås det samme uttrykket, klatring i N omvendt med hensyn til den vertikale aksen.

Konvolusjon

Å jage lignende mål som i Laplace -transformasjonen, konvolusjon av funksjoner refererer til produktet mellom Fourier -transformasjonene. Konvolusjonen gjelder også for diskrete tider og er ansvarlig for mange moderne prosedyrer.

X_n * R_n → F [x_n] .F [r_n]; Transformasjonen av en konvolusjon er lik produktet av de som er transformert.

X_n . R_n→ F [x_n] * F [r_n]; Transformasjonen av et produkt er lik konvolusjonen til de transformerte.

Forskyvning

X_N-m → F [x_k] e ^{-I (2π/n) km} ; Hvis en rekkefølge blir forsinket i M -prøver, vil dens virkning på den diskrete transformasjonen være en modifisering av vinkelen definert av (2π/n) km.

Kan tjene deg: Hvorfor er algebra viktig i visse hverdagslivssituasjoner?

Symmetri konjugert

X_t [-K] = x*_t[k] = x_t [N - k]

Modulasjon

W^-nm_N . x [n] ↔ x_t[K - m]

Produkt

x [n] y [n] ↔ (1/n) x_t[k]*og_t[K]

Symmetri

X [-n] ↔ x_t[-K] = x*_t[K]

Konjugat

x*[n] ↔ x*_t[-K]

ParseVal ligning 

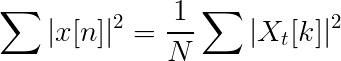
Likheter og forskjeller med Fourier -transformasjonen

Når det gjelder den konvensjonelle transformasjonen av Fourier, har den flere likheter og forskjeller. Fouriers transformasjon konverterer en sekvens til en kontinuerlig linje. På denne måten sies det at resultatet av Fourier -variabelen er en kompleks ekte variabel funksjon.

Fouriers diskret transformasjon, i motsetning til, mottar et diskret signal og forvandler det til et annet diskret tegn, det vil si en sekvens.

Hva er bruken av Fouriers diskrete transformasjon?

De tjener hovedsakelig til betydelige ligninger, mens de transformerer uttrykk avledet til maktelementer. Betegner differensielle uttrykk i former for integrerbare polynomer.

I optimalisering, modulering og modellering av resultater fungerer det som et standardisert uttrykk, og er en hyppig ressurs for prosjektering etter flere generasjoner.

Kilde: Pixabay

Historie

Dette matematiske konseptet ble presentert av Joseph B. Fourier i 1811, mens han utviklet en traktat om Varme spredt. Det ble raskt adoptert av forskjellige grener av vitenskap og ingeniørfag.

Det ble etablert som hovedarbeidsverktøyet i studiet av ligninger med delvis derivater, og sammenlignet selv med arbeidsforholdet mellom Laplace transformerte og vanlige differensialligninger.

Enhver funksjon som kan arbeides med Fourier Transform, må presentere ugyldighet utenfor en definert parameter.

Fourier diskret transformert og dens inverse

Den diskrete transformasjonen oppnås gjennom uttrykket:

Etter en diskret sekvens x [n]

Det inverse av Fouriers diskrete transformasjon er definert gjennom uttrykket:

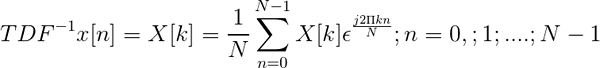Inverse tdf

Det tillater når den diskrete transformeres, definerer sekvensen i tidsdomenet x [n].

Fineri

Parameteriseringsprosessen som tilsvarer Fouriers diskrete transformasjon ligger i Cub. For å jobbe transformasjonen må vi begrense sekvensen i tid. I mange tilfeller har ikke de aktuelle signalene disse begrensningene.

En rekkefølge som ikke oppfyller størrelseskriteriene for å gjelde for den diskrete transformasjonen, kan multipliseres med et "vindu" v [n] -funksjon, og definerer oppførselen til suksessen i en kontrollert parameter.

Kan tjene deg: sirkulære permutasjoner: demonstrasjon, eksempler, løste øvelser

X [n] . V [n]

Spektrumbredden vil være avhengig av vindusbredden. Når vindusbredden øker, vil den beregnede transformerte være smalere.

applikasjoner

Beregning av den grunnleggende løsningen

Fouriers diskrete transformasjon er et kraftig verktøy i studiet av diskrete suksesser.

Fouriers diskret transformasjon transformerer en kontinuerlig variabel funksjon, til en diskret variabel transformasjon.

Cauchys problem for varme ligning presenterer et hyppig anvendelsesfelt av Fouriers diskret transformasjon. Der funksjonen genereres Dirichlet Heat eller Core Nucleus, som gjelder verdier prøvetaking i en definert parameter.

Signalteori

Den generelle årsaken til anvendelsen av Fouriers diskrete transform.

Det kan være en lydbølge eller en elektromagnetisk bølge, Fouriers diskrete transformasjon uttrykker den i en enkel bølgeoverlapping. Denne representasjonen er ganske hyppig i elektroteknikk.

Fouriers serie

De er definert serier når det gjelder cosenos og bryster. De tjener til å lette arbeidet med generelle periodiske funksjoner. Når de brukes, er de en del av oppløsningsteknikkene for delvise og vanlige differensialligninger.

Fourier -serien er enda mer generelle enn Taylors serie, fordi de utvikler periodiske Discontinua -funksjoner som ikke har noen representasjon i Taylor Series.

Andre former for Fourier -serien

Å analytisk forstå Fouriers transformasjon er det viktig.

-Fourier -serien på en 2L -periodefunksjon:

Mange ganger er det nødvendig å tilpasse strukturen i en Fourier-serie, til periodiske funksjoner hvis periode er p = 2l> 0 i intervallet [-l, l].

-Fourier -serien i jevn og rare funksjoner

Intervallet [-π, π] vurderes som gir fordeler når du utnytter funksjonens symmetriske egenskaper.

Kan tjene deg: endelig sett: egenskaper, eksempler, løste øvelser

Hvis f er dreiemoment, er Fourier -serien etablert som en serie Cosenos.

Hvis F er merkelig, er Fourier -serien etablert som en serie bryster.

-Kompleks notasjon av Fourier -serien

Hvis du har en F (t) -funksjon, som oppfyller alle kravene i Fourier-serien, er det mulig å betegne den i intervallet [-t, t] ved å bruke dens komplekse notasjon: 

Eksempler

Når det gjelder beregningen av den grunnleggende løsningen, presenteres følgende eksempler:

Laplace ligning

Varm ligning

Schrödinger ligning

Bølge ligning

På den annen side er det eksempler på anvendelse av Fouriers diskrete transformasjon innen signalteori:

-Systemidentifikasjonsproblemer. Etablert f og g

-Problem med konsistensen av utgangssignalet

-Problemer med signalfiltrering

Øvelser

Oppgave 1

Beregn Fouriers diskrete transformasjon for følgende suksess.

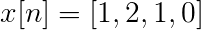
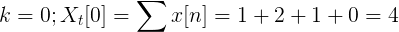
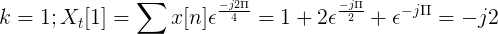
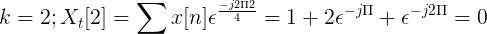
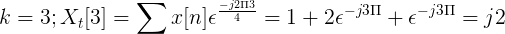
X [n] TDF kan defineres som:

X_t[k] = 4, -j2, 0, j2 for k = 0, 1, 2, 3

Oppgave 2

Det er ønsket å bestemme gjennom en digital algoritme spektralsignalet definert av uttrykket x (t) = e^-t. Der den maksimale frekvensen som ber om koeffisient er f_m= 1Hz. En harmonisk tilsvarer F = 0.3 Hz. Feilen er begrenset til mindre enn 5%. Regne ut F_s , D og n.

Tar hensyn til prøvetakingsteoremet F_s = 2f_m = 2 Hz

En frekvensoppløsning av F₀ = 0.1 Hz, hvor d = 1/0,1 = 10 er oppnådd

0.3 Hz er frekvensen som tilsvarer indeks k = 3, der n = 3 × 8 = 24 prøver. Indikerer det F_s = N/d = 24/10 = 2.4> 2

Fordi formålet er å oppnå minst mulig verdi for n, kan følgende verdier betraktes som en løsning:

F₀ = 0.3 Hz

D = 1/0.3 = 3.33S

K = 1

N = 1 × 8 = 8

Referanser

1. Å mestre den diskrete Fourier -transformasjonen i en, to eller flere dimensjoner: fallgruver og gjenstander. Isaac Amidor. Springer Science & Business Media, 19. juli. 2013
2. DFT: En eierhåndbok for den diskrete Fourier -transformasjonen. William L. Briggs, Van Emden Henson. Siam, 1. jan. nitten nitti fem
3. Digital signalbehandling: teori og praksis. D. Sundararajan. World Scientific, 2003
4. Transforms og raske algoritmer for signalanalyse og representasjoner. Guoan Bi, Yonghong Zeng. Springer Science & Business Media, 6. desember. 2012
5. Diskrete og kontinuerlige Fourier -transformasjoner: Analyse, applikasjoner og raske algoritmer. Eleanor Chu. CRC Press, 19. 2008