Escaleno trapezio egenskaper, formler og ligninger, eksempler

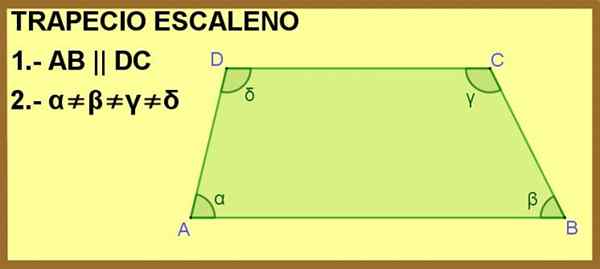
EN trapes Scalene Det er en fire -sidig polygon, hvorav to er parallelle med hverandre, og med sine fire indre vinkler med forskjellige tiltak.

ABCD -kvadrilateral vises, der sidene AB og DC er parallelle med hverandre. Med dette er det nok til å gjøre det til en trapes, men i tillegg er α-, β-, γ- og Δ innvendige vinkler alle forskjellige, derfor er trapesformet Escalano.

Figur 1. ABCD Quadrilateral er en trapes for tilstand 1 og skalen for tilstand 2. Kilde: f. Zapata.

[TOC]

Elementer av Scaleno Trapect

Under de mest karakteristiske elementene:

-Baser og side: De parallelle sidene av trapesiden er basene og de to ikke -parallelle sidene er sidene.

I en Scalene Trapezio er basene også av forskjellige lengder og sidene. Imidlertid kan en scalene trapezoid ha en side av like lengde som en base.

-Median: Det er segmentet som blir med på midtpunktene på sidene.

-Diagonal: Diagonalen til en trapes er segmentet som blir sammen med to motsatte hjørner. En trapes, som hver firkantet, har to diagonaler. I Scalene Trapezio er de av forskjellig lengde.

Andre trapesoider

I tillegg til Escaleno Trapezio, er det andre spesielle trapezoider: rektangelet trapesoid og isosceles trapesidzoid.

Et trapes er rektangel når en av vinklene er rette, mens Trapezio Isosceles har sidene av samme lengde.

Den trapesformen har mange applikasjoner på design- og industrinivå, for eksempel i konfigurasjonen av flymurer, formen på hverdagsobjekter som tabeller, sikkerhetskopiering av stoler, containere, lommebøker, tekstiltrykk og mer.

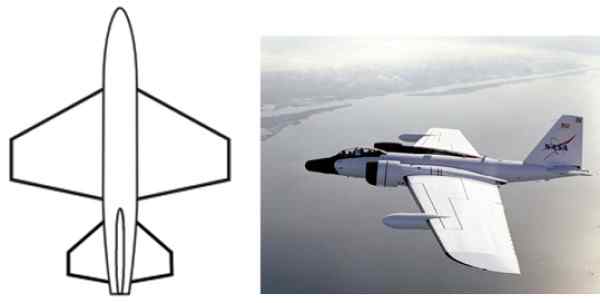Figur 2. Den trapesformen er vanlig i ALAR -flykonfigurasjonen. Kilde: Wikimedia Commons.

Egenskaper

Deretter er egenskapene til klatring av trapesoid oppført, hvorav mange er omfattende til de andre typene trapesoid. I det følgende, når du snakker om “Trapezio”, vil eiendommen være gjeldende for noe slag, inkludert Scalene.

1. Medianen av trapesiden, det vil si segmentet som forener midtpunktene til dets ikke -parallelle sider, er parallelt med noen av basene.

2.- Median av en trapesoid har en lengde som er semi -sum i basene og kutter diagonalene på midtpunktet.

3.- Diagonalene til en trapes krysser hverandre på et punkt som deler dem i to seksjoner som er proporsjonale med forholdet mellom basene.

4.- Summen av rutene til diagonalene til en trapes er lik summen av rutene på sidene pluss det doble produktet av basene.

5.- Segmentet som blir med i midten av diagonale punkter har lengde lik semi -referansen til basene.

Kan tjene deg: Injeksjonsfunksjon: Hva den består av, hva er det for og eksempler

6.- Vinklene ved siden av sidene er supplerende.

7.- I en scalene trapes er lengden på diagonalene forskjellige.

8.- En trapes har bare en registrert omkrets hvis summen av basene er lik summen av sidene.

9.- Hvis en trapes har en registrert omkrets, er vinkelen med toppunkt i midten av nevnte omkrets og sider som passerer gjennom endene av lateralen av trapesen rett.

10.- En escaleno trapes har ingen omskrevet omkrets, den eneste typen trapes som hvis den har det er Isosceles.

Formler og ligninger

Følgende forhold til klatring trapesen henvises til følgende figur.

1.- Hvis ae = ed og bf = fc → ef || AB og EF || DC.

2.- EF = (AB + DC)/2 som er: M = (A + C)/2.

3.- Di = ib = d₁ /2 og ag = gc = d₂ /2.

4.- Dj / jb = (c / a) Tilsvarende cj / ja = (c / a).

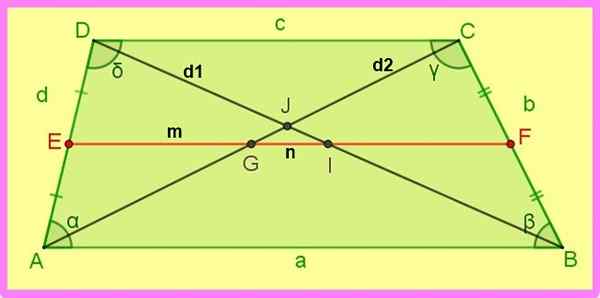Figur 3. Median og diagonaler av en scalene trapezoid. Kilde: f. Zapata.

5.- Db² + Ac² = Annonse² + BC² + 2 AB ∙ DC 

Tilsvarende:

d₁² + d₂² = d² + b² + 2 A ∙ C

6.- GI = (AB - DC)/2

Det er å si:

n = (a - c)/2

7.- α + Δ = 180⁰ og β + γ = 180⁰

8.- Hvis α ≠ β ≠ γ ≠ Δ, så d1 ≠ d2.

9.- Figur 4 viser en scalene trapesoid som har en registrert omkrets, i så fall er det oppfylt at:

A + C = D + B

10.- I en ABCD Escalene trapezoid med et registrert senter av senteret eller følgende er også oppfylt:

∡AOD = ∡BOC = 90⁰

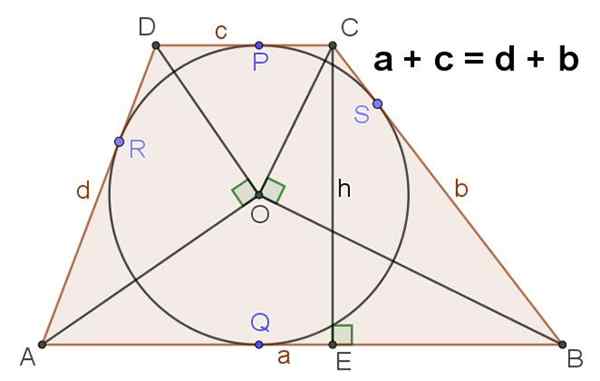Figur 4. Hvis det i en trapes er bekreftet at summen av basene er lik summen av sidene, så er det omkretsen påskrevet i samme. Kilde: f. Zapata.

Høyde

Høyden på en trapes er definert som segmentet som går fra et punkt i basen vinkelrett til motsatt base (eller dets forlengelse).

Alle trapeshøydene har samme tiltak H, så mesteparten av tiden refererer ordhøyden til dets måling. Kort sagt, høyden er avstanden eller separasjonen mellom basene.

Høyden H kan bestemmes om lengden på en side og et av vinklene ved siden av siden er kjent:

H = d sin (α) = d sin (γ) = b Sin (β) = B sin (Δ)

Median

M -medianmålet på trapesoiden er semi -kroppene til basene:

M = (a + b)/2

Diagonaler

d₁ = √ [a² + d² - 2 ∙ a ∙ d ∙ cos (α)]

d₂= √ [a² + b² - 2 ∙ A ∙ B ∙ COS (β)]

Det kan også beregnes hvis bare lengden på trapesformet er kjent:

d₁ = √ [B² + A ∙ C - A (B² - d²)/(a - c)]

d₂ = √ [D² + A ∙ C - A (D² - b²)/(a - c)]

Omkrets

Omkretsen er den totale lengden på konturen, det vil si summen av alle sidene:

Kan tjene deg: diskret tilfeldig variabel

P = a + b + c + d

Område

Området til en trapezoid er semi -kroppene til basene multiplisert med høyden:

A = h ∙ (a + b)/2

Det kan også beregnes hvis median m og høyde er kjent:

A = m ∙ h

I tilfelle bare lengden på trapesidene er kjent, kan området bestemmes av Heróns formel for trapesiden:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]

Hvor s er semi -perimeter: s = (a+b+c+d)/2.

Andre forhold for klatringstigningen

Medianens kutt med diagonalene og parallellen som går gjennom skjæringspunktet mellom diagonalene, gir opphav til andre forhold.

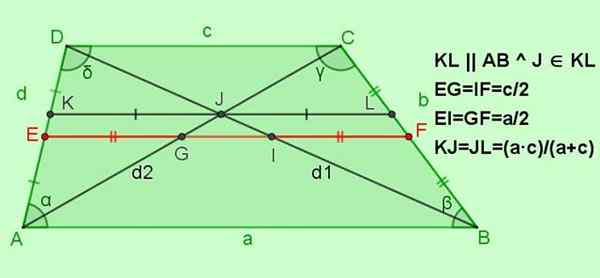Figur 5. Andre forhold for klatringstigningen. Kilde: f. Zapata.

-Forhold for median EF

EF = (A+C)/2; F.eks = if = c/2; Ei = gf = a/2

-Relasjoner for det parallelle segmentet til KL -basene, og det går gjennom punktet av Kryss J av diagonalene

Ja KL || Ab || DC med J ∈ KL, deretter KJ = JL = (A ∙ C)/(A+C)

Bygging av Scalene Trapezium med regel og kompass

Gitt basene i lengden til og c, å være en> c og med side av lengden B og d, å være b> d, Vi fortsetter å følge disse trinnene (se figur 6):

1.- Med regelen er segmentet av den største AB trukket.

2.- Fra en SE og på AB er punkt P merket slik at AP = C.

3.- Med kompasset med C- og Radio D -senteret trekkes en bue.

4.- Det er laget sentrum i B med radio B som tegner en bue som tolker buen trukket opp i forrige trinn. Vi kaller at kryssingspunktet.

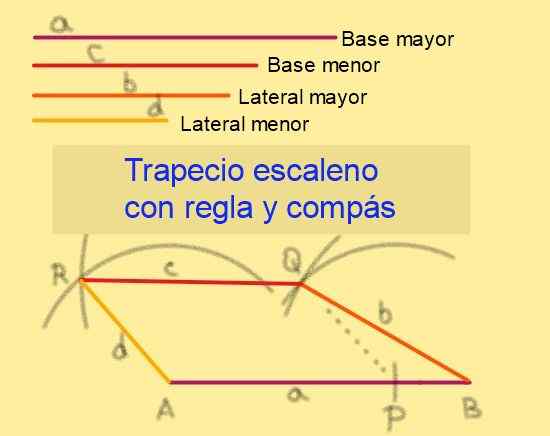Figur 6. Bygging av Escaleno Trapecio gitt sidene. Kilde: f. Zapata.

5.- Med sentrum i å tegne en radiusbue d.

6.- Med sentrum å tegne en radiusbue som ble oppfanget til buen trukket opp i forrige trinn. Det vil bli kalt r til skjærepunktet.

7.- Segmentene BQ, QR og RA er tegnet med regelen.

8.- ABQR Quadrilateral er en skalae trapesoid, siden APQR er et parallellogram, som garanterer at AB || QR.

Eksempel

Følgende lengder er gitt i CM: 7, 3, 4 og 6.

a) Bestem om du med dem kan bygge en Scalene trapes som kan omskrive til en omkrets.

b) Finn omkretsen, området, lengden på diagonalene og høyden på nevnte trapes, samt radius for den registrerte omkretsen.

- Løsning på

Ved å bruke segmentene i lengde 7 og 3 som baser og lengden 4 og 6 som sider, kan en skala -trapezoid bygges ved hjelp av prosedyren beskrevet i forrige seksjon.

Vi må sjekke om den har en registrert omkrets, men husker eiendommen (9):

Kan tjene deg: sekskantet prisme

En trapes har bare en registrert omkrets hvis summen av basene er lik summen av sidene.

Vi ser det faktisk:

7 + 3 = 4 + 6 = 10

Da blir tilstanden til den innskrevne omkretsen oppfylt.

- Løsning b

Omkrets

Operimeter P oppnås ved å legge til sidene. Ettersom basene totalt er 10 og sidene også, er omkretsen:

P = 20 cm

Område

For å bestemme området, bare kjent, er forholdet anvendt:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]

Hvor S er semi -perimeter:

S = (a+b+c+d)/2.

I vårt tilfelle er halvperimeteret verdt S = 10 cm. Etter å ha erstattet de respektive verdiene:

A = 7 cm; B = 6 cm; C = 3 cm; D = 4 cm

Er til overs:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Høyde

Høyde H er relatert til område A gjennom følgende uttrykk:

A = (a+c) ∙ h/2, hvor høyden kan oppnås ved klarering:

H = 2a / (a+c) = 2 * 19,84 / 10 = 3,968 cm.

Registrert omkretsradio

Radius for den registrerte omkretsen er verdt halvparten av høyden:

R = h/2 = 1 984 cm

Diagonaler

Endelig er det lengden på diagonalene:

d₁ = √ [B² + A ∙ C - A (B² - d²)/(a - c)]

d₂ = √ [D² + A ∙ C - A (D² - b²)/(a - c)]

Riktig erstatning av verdiene er:

d₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

d₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

Det vil si: D₁ = 4,69 cm og d₂ = 8,49 cm

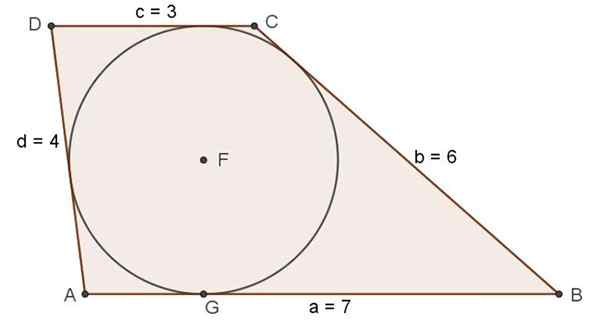Figur 7. Scalene Trapezio som oppfyller tilstanden til eksistensen av registrert omkrets. Kilde: f. Zapata.

Trening løst

Bestem de indre vinklene til basen trapesoid ab = a = 7, cd = c = 3 og lateral bc = b = 6, da = d = 4.

Løsning

Kosinusteoremet kan brukes for å bestemme vinklene. For eksempel bestemmes vinkelen ∠A = α fra trekanten ABD med AB = A = 7, BD = D2 = 8,49 og DA = D = 4.

Kosinosteoremet som ble brukt på denne trekanten forblir slik:

d₂² = a² + d² - 2 ∙ a ∙ d ∙ cos (α), det vil si:

72 = 49+16-56 ∙ cos (α).

Ved rydding oppnås kosinus av vinkelen α:

Cos (α) = -1/8

Det vil si at α = Arccos (-1/8) = 97.18⁰.

På samme måte oppnås de andre vinklene, og er deres verdier:

β = 41.41⁰; γ = 138,59⁰ og til slutt Δ = 82,82⁰.

Referanser

1. C. OG. TIL. (2003). Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematikk 2. Patria redaksjonell gruppe.
3. Frigjort, k. (2007). Oppdag polygoner. Benchmark Education Company.
4. Hendrik, v. (2013). Generaliserte polygoner. Birkhäuser.
5. Iger. (s.F.). Matematikk første semester Tacaná. Iger.
6. JR. Geometri. (2014). Polygoner. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematikk: Resonnement og applikasjoner (tiende utgave). Pearson Education.
8. Patiño, m. (2006). Matematikk 5. Redaksjonell progreso.
9. Wikipedia. Trapes. Gjenopprettet fra: er.Wikipedia.com