Trapecio isosceles egenskaper, forhold og formler, eksempler

EN trapes likebent Det er en firkantet der to av sidene er parallelle med hverandre, og også de to vinklene ved siden av en av de parallelle sidene har samme mål.

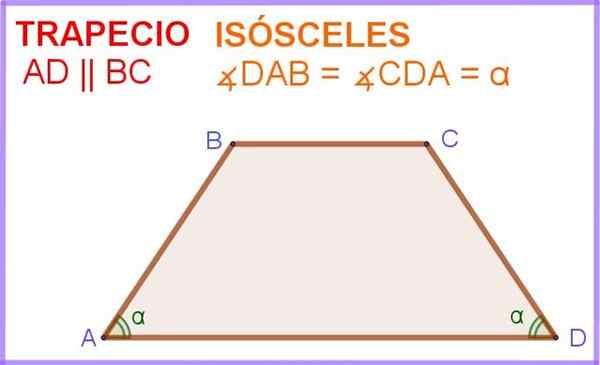
I figur 1 har du ABCD -firkantet, der AD- og BC -sidene er parallelle. I tillegg har vinklene ∠DAB og ∠ADC ved siden av den parallelle sideannonsen samme mål α. 

Figur 1. Trapezium isosceles. Kilde: f. Zapata.

Dermed er denne firkantede, eller fire -sidige polygonen, faktisk en isosceles trapesidzoid.

I en trapes kalles de parallelle sidene baser og ikke-paralleller kalles lateral. En annen viktig funksjon er høyde, som er avstanden som skiller parallelle sider.

I tillegg til isosceles trapesoid er det andre typer trapes:

-TRapecio Escaleno, som har alle forskjellige vinkler og sider.

-TRektangel Rapecio, der en side har rette tilstøtende vinkler.

Den trapesformen er hyppig på forskjellige områder av design, arkitektur, elektronikk, beregning og mange flere, som det vil bli sett senere. Derav viktigheten av å bli kjent med dens egenskaper.

[TOC]

Egenskaper

EKSKLUSIV ISOSCELES TRAPEZOID

Hvis en trapes er isosceles, oppfyller følgende karakteristiske egenskaper:

1.- Sidene har samme mål.

2.- Vinklene ved siden av basene er de samme.

3.- Motsatte vinkler er supplerende.

4.- Diagonalene har samme lengde, det samme er de to segmentene som forener de motsatte toppunktene.

5.- Vinkelen som dannes mellom basene og diagonalene er alle av samme mål.

6.- Det har omskrevet omkrets.

Gjensidig, hvis en trapeze møter noen av de tidligere egenskapene, er det en isosceles trapesoid.

Hvis en av vinklene er rett (90 º i en trapesel. Det vil si at et rektangel er et spesielt tilfelle av isosceles trapesidzoid.

Figur 2. Corn Palomites -beholderen og skolebordene er formet som Isosceles. Kilde: PXFuel (til venstre)/McDowell Craig gjennom Flickr. (Ikke sant)

For alle trapesformet

Følgende sett med egenskaper er gyldige for all trapes:

7.- De median Av trapesen er det segmentet som sammenføyer midtpunktene til dets ikke -parallelle sider, er parallell med noen av basene.

8.- Lengden på medianen er lik halvtemumet (sum delt med 2) av den for dens baser.

9.- Medianen av en trapesoid kutter diagonalene ved midtpunktet.

10.- Diagonalene til en trapes krysser hverandre på et punkt som deler dem i to seksjoner proporsjonale med basenes kvotienter.

elleve.- Summen av rutene til diagonalene til en trapes er lik summen av rutene på sidene pluss det doble produktet av basene.

Det kan tjene deg: Hvor mange tusendeler passer de i en tiende?

12.- Segmentet som blir med i midten av diagonale punkter har lengde lik semi -referansen til basene.

1. 3.- Vinklene ved siden av sidene er supplerende.

14.- En trapes har en registrert omkrets hvis og bare hvis summen av basene er lik summen av sidene.

femten.- Hvis en trapes har en registrert omkrets, er vinklene med toppunkt i midten av nevnte omkrets og sider som går gjennom endene på samme side, rette vinkler.

Relasjoner og formler

Følgende sett med forhold og formler blir referert til figur 3, hvor i tillegg til isosceles trapesoid andre viktige segmenter som allerede er nevnt, for eksempel diagonaler, høyde og medium.

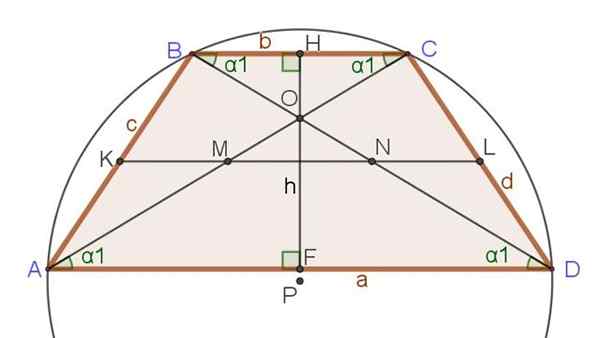Figur 3. Median, diagonaler, høyde og omkrets omskrevet i en isosceles trapesoid. Kilde: f. Zapata.

Eksklusive forhold til Isosceles Trapecio

1.- Ab = dc = c = d

2.- ∡dab = ∡cda og ∡abc = ∡bcd

3.- ∡dab + ∡bcd = 180º og ∡cda + ∡abc = 180º

4.- BD = AC

5.- ∡CAD = ∡BDA = ∡CBD = ∡BCA = α₁

6.- A, B, C og D tilhører den omskrevne omkretsen.

Relasjoner for enhver trapesoid

7. Hvis AK = KB og DL = LC ⇒ KL || AD og KL || BC

8.- KL = (AD + BC)/2

9.- AM = MC = AC/2 og DN = NB = DB/2

10.- AO/OC = AD/BC Y DO/OB = AD/BC

elleve.- Ac² + Db² = Ab² + DC² + 2⋅ad⋅bc

12.- MN = (AD - BC)/2

1. 3.- ∡DAB + ∡ABC = 180º og ∡CDA + ∡BCD = 180º

14.- Hvis AD + BC = AB + DC ⇒ ∃ R hva likestilling av AD, BC, AB og DC

femten.- Hvis ∃ r hva ekvidista av ad, BC, AB og DC, da:

∡bra = ∡drc = 90º

Isosceles trapesforhold med registrert omkrets

Hvis summen av basene er i en isosceles -trapes.

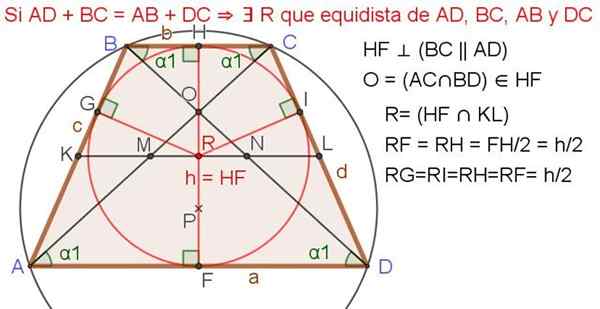Figur 4. Trapeze med registrert omkrets. Kilde: f. Zapata.

Følgende egenskaper gjelder når isosceles trapesoid har en registrert omkrets (se figur 4 ovenfor):

16.- Kl = AB = DC = (AD + BC)/2

17.- Diagonalene er kuttet i rett vinkel: AC ⊥ BD

18.- Høyden er den samme som median: hf = kl, det vil si h = m.

19.- Square of the Height er lik produktets produkt: h² = BC⋅ad

tjue.- Under disse spesifikke forholdene er trapesområdet lik kvadratet på høyden eller produktets produkt: område = h² = BC⋅ad.

Formler for å bestemme den ene siden, kjent de andre og en vinkel

Kjent en base, siden og en vinkel, kan den andre basen bestemmes av:

a = b + 2c cos α

B = a - 2c cos α

Hvis lengden på basene er kjent som kjent og en vinkel, er lengden på begge sider:

Det kan tjene deg: Fermat Limit: Det som består av øvelser løst

C = (a - b) / (2 cos α)

Besluttsomhet på den ene siden, kjent de andre og en diagonal

A = (D₁² - c²)/ B;

B = (D₁² - c²)/ til 

C = √ (D₁² - A⋅B)

Hvor₁ Det er lengden på diagonalene.

Base fra høyden, området og den andre basen

a = (2 a)/h - b

b = (2 a)/h - a

Kjent baser, området og en vinkel

C = (2a) /[(a + b) sin α]

Kjent lateral median, området og en vinkel

C = a / (m.sin α)

Kjent høyde sidene

H = √ [4 c² - (A - B)²]

Kjent høyde en vinkel og to sider

H = tg ⋅⋅ (a - b)/2 = c . sin α

Kjente diagonaler alle sider, eller to sider og en vinkel

d₁ = √ (C²+ a b)

d₁ = √ (a²+ c² - 2 a c cos α)

d₁ = √ (B² + c²- 2 B C COS β)

Isosceles Triangle Operimeter 

P = A + B + 2C

Isosceles trapezoid område

Det er flere formler for å beregne området, avhengig av dataene som er kjent. Følgende er det mest kjente, avhengig av baser og høyde:

A = h⋅ (a + b)/2

Og disse andre kan også brukes:

-Hvis sidene er kjent

A = [(a +b)/4] √ [4c² - (A - B)²]

-Når du har to sider og en vinkel

A = (b + c cos α) c sen α = (a - c cos α) c sen α

-Hvis radien til den registrerte omkretsen er kjent og en vinkel

A = 4 r² / Sin α = 4 r² / Sin β

-Når basene og en vinkel er kjent

A = a⋅b / sin α = a⋅b / sen β 

-Hvis trapesen kan registreres en omkrets

A = c⋅ √ (a⋅b) = m⋅ √ (a⋅b) = r⋅ (a + b)/2

-Kjent diagonalene og vinkelen som dannes med hverandre

A = (D₁²/2) sen γ = (d₁² / 2) Sen Δ 

-Når du har siden, medianen og en vinkel

A = MC.sin α = mc.Sen β

Omskrevet omkretsradio

Bare isosceles trapesoider har en omskrevet omkrets. Hvis hovedbasen er kjent, er siden C og diagonalen d₁, Da er radius r av omkretsen som passerer gjennom de fire hjørnene til trapesen:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p -d₁)]

Hvor p = (a + c + d₁) / 2

Eksempler på bruk av isosceles trapesoid

Isosceles trapesoid vises innen designfeltet, som sett i figur 2. Og her har vi noen flere eksempler:

I arkitektur og konstruksjon

De gamle inkaene kjente Isosceles trapesoid og brukte det som et konstruksjonselement i dette vinduet i Cuzco, Peru:

Figur 5 . Vindu med en trapesformet form av Coricancha, Cuzco. Kilde: Wikimedia Commons.

Og her vises trapezoiden igjen i samtalen Trapezoidal ark, Et ofte brukt materiale i konstruksjon:

Figur 6. Trapezoidal metallplate beskytter vinduene i en bygning midlertidig. Kilde: Wikimedia Commons.

I design

Vi så allerede at Isosceles trapesoid vises i hverdagsobjekter, inkluderende matvarer som denne sjokoladebaren:

Figur 7. Sjokoladebar hvis ansikter er formet som isosceles. Kilde: PXFuel.

Løste øvelser

- Oppgave 1

En isosceles trapezoid er basert enn 9 cm, base mindre enn 3 cm og diagonalene 8 cm hver. Regne ut:

Det kan tjene deg: Generell parabola -ligning (eksempler og øvelser)

a) side

b) høyde

c) Omkrets

d) ärea

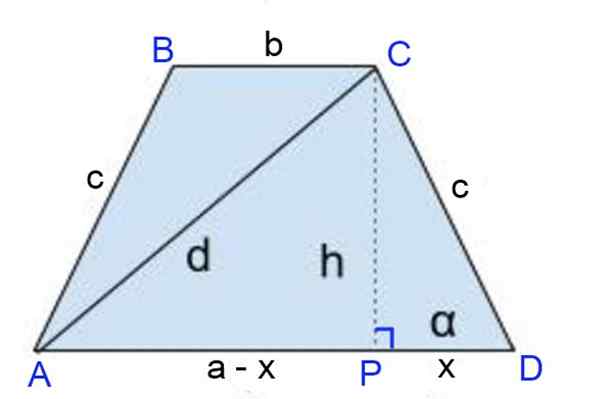Figur 8. Ordning for oppgave 1. Kilde: f. Zapata

Løsning på

Høyden CP = H er tegnet, der høydenes fot definerer segmentene:

Pd = x = (a-b)/2 og 

Ap = a - x = a - a/2 + b/2 = (a + b)/2.

Gjennom Pythagoras -teorem til DPC -rektangel -trekanten:

c² = h² + (A - B)² /4

Og også til APC Rectangle Triangle:

d² = h² + Ap² = h² + (A+B)² /4

Til slutt blir et medlem trukket fra, den andre ligningen av den første og forenkler:

d² - c² = ¼ [(a+b)² - (A-B)²] = ¼ [(a+b+a-b) (a+b-a+b)]

d² - c² = ¼ [2a 2b] = a b

c²= d² - A b ⇒ c = √ (d² - a b) = √ (8² - 9⋅3) = √37 = 6,08 cm

Løsning b

h² = d² - (A+B)² /4 = 8² - (12² / 2² ) = 8² - 6² = 28

H = 2 √7 = 5,29 cm

Løsning c

Omkrets = A + B + 2 C = 9 + 3 + 2⋅6,083 = 24,166 cm

Løsning d

Område = H (A+B)/2 = 5,29 (12)/2 = 31,74 cm

- Oppgave 2

Det er en isosceles trapezoid hvis største base er dobbelt så langt og den minste basen er lik høyden, som er 6 cm. Fastslå:

a) siden av siden

b) Omkrets

c) område

d) vinkler

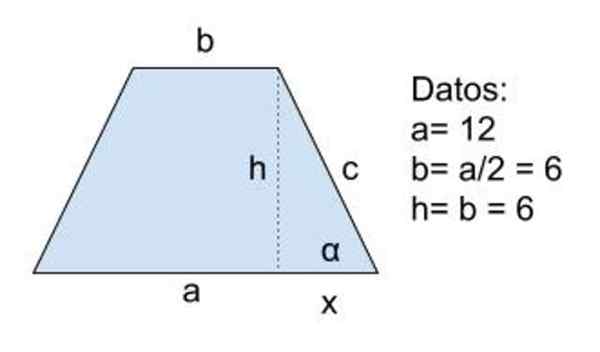Figur 8. Ordning for oppgave 2. Kilde: f. Zapata

Løsning på

Data: a = 12, b = a/2 = 6 og h = b = 6

Vi fortsetter på denne måten: høyden h trekkes og Pythagoras -teoremet brukes på hypotenuse -trekanten "C" og Catetos H og X:

c² = h²+Xc²

Da må du beregne høydeverdien fra dataene (h = b) og kateto x: 

a = b + 2 x ⇒ x = (a-b)/2

Erstatte de tidligere uttrykkene du har:

c² = b²+(A-B)²/2²

Nå blir numeriske verdier introdusert og forenklet:

c² = 62+ (12-6) 2/4

c² = 62 (1+¼) = 62 (5/4)

Å skaffe seg:

C = 3√5 = 6,71 cm

Løsning b

Omkretsen P = A + B + 2 C

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Løsning c

Området basert på høyden og lengden på basene er:

A = h⋅ (a + b)/2 = 6⋅ (12 + 6)/2 = 54 cm²

Løsning d

Vinkelen α som danner siden med hovedbasen oppnås ved trigonometri:

Solbrun (α) = h / x = 6/3 = 2

α = Arctan (2) = 63,44º

Den andre vinkelen, som danner siden med den mindre basen er β, som er supplerende av α:

β = 180º - α = 180º - 63,44º = 116,56º

Referanser

1. OG. TIL. 2003. Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
2. Campos, f. 2014. Matematikk 2. Patria redaksjonell gruppe.
3. Frigjort, k. 2007. Oppdag polygoner. Benchmark Education Company.
4. Hendrik, v. 2013. Generaliserte polygoner. Birkhäuser.
5. Iger. Matematikk første semester Tacaná. Iger.
6. JR. Geometri. 2014. Polygoner. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. 2006. Matematikk: resonnement og applikasjoner. 10.  Utgave. Pearson Education.
8. Patiño, m. 2006. Matematikk 5. Redaksjonell progreso.
9. Wikipedia. Trapes. Gjenopprettet fra: er.Wikipedia.com