Tidecágono

Figur 1.- Til venstre en vanlig tridecácágone og til høyre en valuta på 20 kroner i Tsjekkia, med en bridecagon -form formet kontur påskrevet i en omkrets, på den ene siden har den løven av Bohemia og på den andre til San Wenceslao, skatron av Tsjekkia, montert på hesteryggen. Kilde: f. Zapata.

Hva er en tridecágono?

Tridecagon er en flat geometrisk figur av Polygons -familien, og som er preget av å ha 13 sider og 13 hjørner. Et annet navn for denne polygonen er Triskaidcágono, Antall avledet fra gresk.

De 13 sidene er linjesegmenter som endelig nærmer seg figuren. Polygonene, som er navngitt i henhold til mengden sider, er en rik inspirasjonskilde for arkitektur, konstruksjon og design av mange gjenstander, både kunst og utilitarikere.

Egenskaper til Tridecágono

Tridecágono deler med de andre polygonene følgende egenskaper og egenskaper:

-Sider, De er linjesegmentene som er sammenføyd for å danne figuren, som i tilfelle av Tridecágono er 13. De identifiseres med små bokstaver.

-Hjørner, Dette er hva skjæringspunktene på påfølgende sider kalles og betegner vanligvis med store bokstaver. Tridecágono har 13 hjørner.

-Omkrets, tilsvarer summen av sidene. Hvis alle sider har like mål “A”, er omkretsen ganske enkelt 13 × A, men hvis sidene er ulik, legger omkretsen til hver av sidene på sidene.

-Senter, Det er poenget som holder samme avstand med både toppunktene og sidene.

-Diagonal, En linje som blir med i et toppunkt til et annet ikke -samlet toppunkt (de påfølgende vertiklene er forent av sidene).

-Interne vinkler, De er dannet mellom to tilstøtende sider av figuren og på den indre delen av polygonen, og dets toppunkt er den vanlige toppunktet til begge sider.

Kan tjene deg: Miletus slikt teorem

-Eksterne vinkler, De er utenfor polygonen, mellom den ene siden og forlengelsen av en av påfølgende sidene til den første.

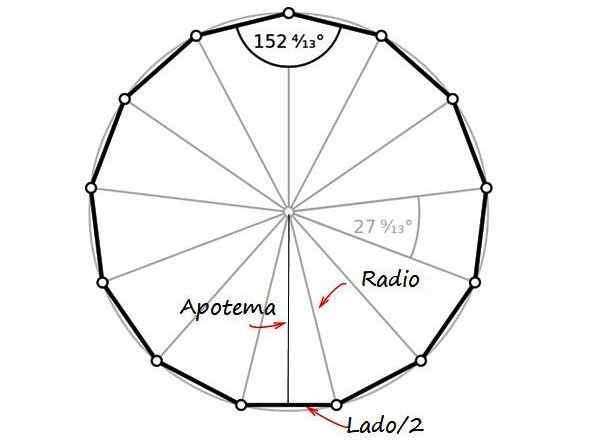
-Radio, Avstandsavstand-vertix av Tridecágon.

-Sentral vinkel, Det er den hvis toppunkt er sentrum av polygonen.

-Apothem, segment som blir med sentrum av den ene siden med midten av figuren og danner 90º med den siden.

Regelmessig og uregelmessig torden

Treekaroner kan være:

-Regelmessig, Når målet på alle sine tretten sider er det samme og dens indre vinkler måler det samme.

-Uregelmessig, Hvis en eller flere av sidene har forskjellige tiltak.

Når det gjelder den vanlige Tridecácágone, kan følgende formler brukes:

Indre vinkel

For en vanlig polygon er formelen som gjør det mulig å beregne verdien av den interne vinkelen:

Der n representerer antall sider, som i dette tilfellet er 13. Med denne verdien er det:

I = (11 × 180º)/13 ≈ 152.3

Diagonaler

Antall diagonaler beregnes med følgende formel, til og med gyldig hvis polygon er uregelmessig:

For n = 13 resultater:

D = 13 × 10/2 = 65 diagonaler

Apothem

Verdien av apothem l_TIL  Det beregnes med følgende formel, og er "en" lengden på siden:

L_TIL ≅ 2.0286A

Område

Hvis omkretsen p og lengden på apothem l_TIL, Tridecágono -området beregnes av:

A = (P × L_TIL)/2

Avhengig av "A" -siden, gjenstår formelen:

A = (13a × l_TIL)/2

Erstatte tiltaket_TIL Fra forrige seksjon oppnås en formel for området som bare avhenger av lengden på siden:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Kan tjene deg: Hypergeometrisk distribusjon: Formler, ligninger, modell

Trening

Hvis diameteren til en 20 mm kroner er 26 mm, hvor mye er siden og området til Tridecágono registrert i sirkelen av valutaen?

Løsning

Fra figuren er det en rektangel -trekant, hvis kategorier er apothem og halvparten av lengden på siden, med hypotenusa lik radiusen til valutaen, som er halvparten av diameteren. Siden dette er verdt 26 mm, er radio r lik 13 mm.

Figur 2. Radioen, apotemen og halvparten av siden av trindecagon danner et rektangel -trekant. Kilde: Wikimedia Commons/F. Zapata.

Av Pythagoras teorem:

Siden l_TIL ≈ 2.0286A, du har:

R² = (2.0286A)² + (0.5.)² = 4.3652a²

Siden er:

Med denne verdien er valutaen:

A ≈ 13.186a² = 13.186 (6.222mm)² = 510.5 mm²

Leseren er igjen for å sammenligne dette resultatet med området oppnådd ved å anta at valutaen er sirkulær av radius r = 13 mm.

Hvordan er en tridecágono?

Den vanlige trindecagon er av polygonene som ikke innrømmer nøyaktig konstruksjon ved å bare regel og kompass, det vil si at det ikke er en byggbar polygon. De er bare byggbare, i det minste i teorien, de polygonene hvis antall sider bare inkluderer primære faktorer i formen:

Primtallene på den måten kalles Fermat Cousins, Men tallet 13, selv om det er fetter, har ikke dette skjemaet.

Imidlertid kan du tegne en vanlig trindecagon som er registrert i en omkrets, hvert toppunkt har kryss med seg, uten å bli lagt merke til i det blotte øye. For dette er det nødvendig.

Kan tjene deg: obtusangle trekant

En måte å bygge en vanlig Tridecácágone, selv om den ikke er den eneste, er å trekke strekene som vist i følgende animasjon:

Figur 3. Bygging av en vanlig tridecagon. Kilde: Wikimedia Commons.

Og denne andre animasjonen beskriver også hvordan man lager en Tridecágono omtrent, med regel og kompass:

Figur 4.- Alternativ måte å bygge en omtrent vanlig tridecagon med regel og kompass på. Kilde: Wikimedia Commons.

Eksempler på Tridecágel

Konkav og konveks torden

Når de indre vinklene til tridecágono er mindre enn 180 º, er figuren konveks, mens hvis en eller flere indre vinkler er større enn 180º, er tridecágono konkav.

Den vanlige Tridecácágon er konveks, siden dens indre vinkler måler omtrent 152.3. hver.

Bruk av Tridecágono i numismatikk

Tsjekkisk krone

Numismatics er vitenskapen om mynter, medaljer, billetter og chips. Polygonene på mange sider er ideelle som dekorative elementer i utformingen av mynter, spesielt de som har mange sider, for eksempel Tridecágono.

Ikke alle mynter er runde, men polygonene på mange sider ligner den sirkulære formen, jo flere sider har den, jo større er tilnærmingen. Derfor bruker Coins -designere polygonene på mange sider for å introdusere et snev av originalitet i designen deres.

Ulike polygoner brukes med dette formålet, for eksempel den øvre valutaen, kalt kronen og fra Tsjekkia, et godt eksempel på bruk av Tridecágono som et designelement.

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Tegning. Vanlige polygoner. Gjenopprettet fra: tegning.com.
3. Hartley, m. Konstruere en tridecagon. Gjenopprettet fra: YouTube.com
4. Wikipedia. Byggbar polygon. Gjenopprettet fra: er.Wikipedia.org.
5. Wikiwand. Tidecagon. Gjenopprettet fra: wikiwand.com.