Scalene Triangle

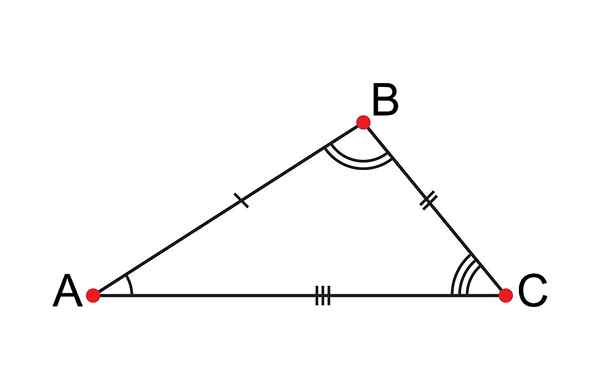
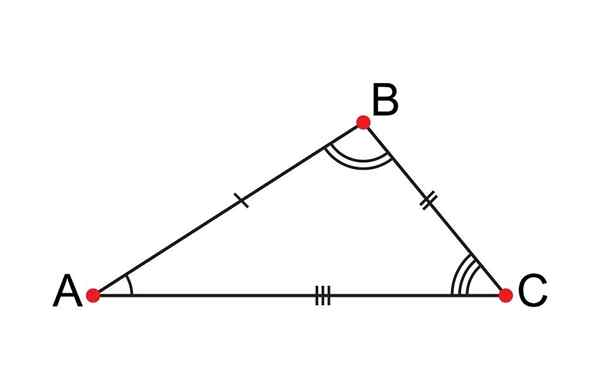Scalene -trekanten har alle sine ulik sider

Hva er en skala trekant?

EN Scalene Triangle Det er en tre -sidig polygon, der alle har forskjellige tiltak eller lengder; Av den grunn ble det gitt navnet Escaleno, som på latin betyr ulik.

Trekantene er polygoner betraktet som de enkleste i geometri, fordi tre sider, tre vinkler og tre hjørner er dannet. I tilfelle av Scalene -trekanten, for å ha alle de forskjellige sidene, innebærer det at de tre vinklene også vil være.

Skala trekanteregenskaper

Skala -trekanter er enkle polygoner fordi ingen av sidene eller vinklene har samme mål, i motsetning til isosceles og likevektstrekanter.

Fordi alle sidene og vinklene har forskjellige tiltak, anses disse trekantene som uregelmessige konvekse polygoner.

I henhold til amplituden av indre vinkler er skalene trekanter klassifisert som:

• Scalene Rectangle Triangle: Alle sidene er forskjellige. Et av vinklene er rette (90^enten) og de andre er akutte og med forskjellige tiltak.
• Scalene stump Triangle: Alle sidene er forskjellige og en av vinklene er stump (> 90^enten).
• Scalene Acutangle Triangle: Alle sidene er forskjellige. Alle dens vinkler er akutte (< 90^enten), Med forskjellige tiltak.

Et annet kjennetegn ved Scalene -trekantene er at på grunn av inkonsisten.

Komponenter/elementer

Medianen

Det er en linje som forlater fra midtpunktet på den ene siden og når motsatt toppunkt. De tre mediene deltar på et punkt som heter baricentro eller centroid.

Bisektoren

Det er en halv rett som deler hver vinkel i to vinkler med like mål. Bisektorene til en trekant er enig i punkt som kalles incenter.

MediaTrix

Det er et segment vinkelrett på siden av trekanten, som har sin opprinnelse midt i dette. Det er tre mediatriser i en trekant og delta på et punkt som kalles circumentro.

Høyden 

Det er linjen som går fra toppunktet til motsatt side, og også denne linjen er vinkelrett på den siden. Alle trekanter har tre høyder som sammenfaller på et punkt som heter Ortotener.

Egenskapene til Escaleno Triange

Skala -trekanter er definert eller identifisert fordi de har flere egenskaper som representerer dem, stammer fra teoriene foreslått av store matematikere. De er:

Interne vinkler

Summen av interne vinkler er alltid lik 180^enten.

Sum av sidene

Summen av tiltakene på to sider skal alltid være større enn målet på tredje side, a + b> c.

Inkongruøse sider

Alle sider av klatrekantene har forskjellige tiltak eller lengder; det vil si at de er inkongruøse.

Inkongruøse vinkler

Siden alle sidene av Scalene -trekanten er forskjellige, vil også vinklene være. Imidlertid vil summen av de indre vinklene alltid være lik 180º, og i noen tilfeller kan en av vinklene være stump eller rett, mens i andre vil alle dens vinkler være akutte.

Kan tjene deg: Multiplikative problemer for barn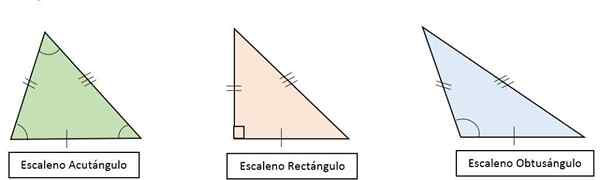 Typer av skaletrekanter i henhold til deres vinkler

Høyde, median, mediatrix og bisektor er ikke tilfeldig

Som enhver trekant har Escaleno forskjellige linjer med linjer som komponerer den, for eksempel: høyde, medium, mediatrix og bisektor.

På grunn av sidene på sidene, vil ingen av disse linjene sammenfatte i en enkelt av en enkelt av disse linjene i en enkelt.

Orocentro, baricentro, incentro og circumcentro er ikke tilfeldig

I likhet med høyden er median, bisektor og mediatrix representert av forskjellige linjesegmenter, i en Scalene -trekant vil møtepunktene -Orthosenteret, incentre og circumentro baricenter -vil bli funnet på forskjellige punkter (det vil si at de ikke sammenfaller).

Avhengig av om trekanten er akutangrep, rektangel eller stump, har ortosenteret forskjellige steder:

til. Hvis trekanten er akutangrep, vil ortosenteret være inne i trekanten.

b. Hvis trekanten er rektangel, vil ortosenteret sammenfalle med toppunktet på rett side.

c. Hvis trekanten er stump, vil ootocenteren være utenfor trekanten.

Relative høyder

Høydene er relativt til sidene.

Når det gjelder Scalene Triangle, vil denne høydene ha forskjellige tiltak. Hver trekant har tre relative høyder og for å beregne dem, brukes Herón -formelen.

Omkretsberegning, område, høyde og sider

Hvordan beregne omkretsen?

Omkretsen til en polygon beregnes av summen av sidene.

Som i dette tilfellet har Scalene -trekanten alle sine sider med et annet tiltak, dens omkrets vil være:

P = side til + side b + side c.

Hvordan beregne området?

Trekantene beregnes alltid med samme formel, multipliserer basen etter høyde og deling med to:

Område = (base _* H) ÷ 2

I noen tilfeller er ikke høyden på Scalene -trekanten kjent, men det er en formel som ble foreslått av matematikeren Herón, for å beregne området og vite målet på de tre sidene av en trekant.

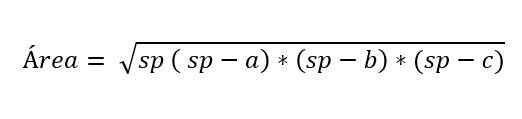
Hvor:

• A, B og C representerer sidene av trekanten.
• SP tilsvarer semi -perimeter av trekanten, det vil si halvparten av omkretsen:

sp = (a + b + c) ÷ 2

I tilfelle at bare to av sidene av trekanten og vinkelen som dannes mellom dem er, kan området beregnes ved å anvende de trigonometriske grunnene. Dermed må du:

Område = (side _* H) ÷ 2

Der høyden (h) er produktet på den ene siden gjennom motsatt vinkel. For eksempel, for hver side, vil området være:

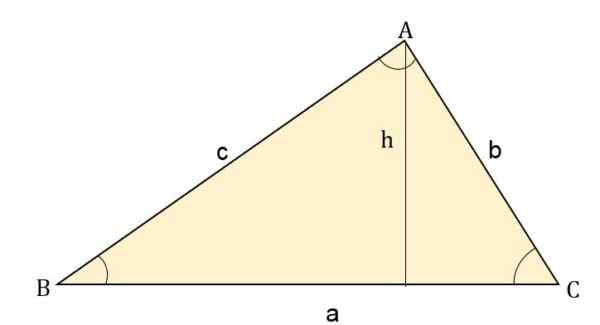
• Område = (B _* c _* sin a) ÷ 2
• Område = (a _* c _* sin b) ÷ 2.
• Område = (a _* b _* Sen c) ÷ 2

Hvordan beregne høyden?

Som alle sidene av Scalene -trekanten er de forskjellige, er det ikke mulig å beregne høyden med Pythagoras teorem.

Fra Herón -formelen, som er basert på tiltakene til de tre sidene av en trekant, kan området beregnes.

Kan tjene deg: Faktoriell notasjon: Konsept, eksempler og øvelser

Høyden kan være klar fra den generelle formelen i området:

Formel for å beregne høyden på en scalene trekant

Siden erstattes av målet på side A, B eller C.

En annen måte å beregne høyden når verdien av et av vinklene er kjent, er å bruke de trigonometriske årsakene, der høyden vil representere en trekantkateto.

For eksempel, når den motsatte vinkelen er kjent for høyden, vil den bli bestemt av brystet:

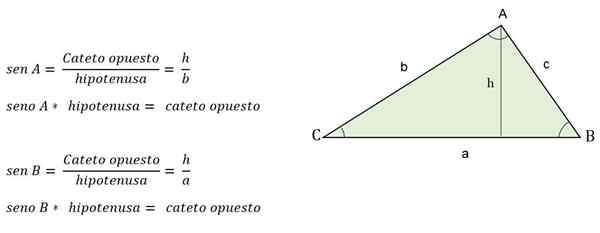Trigonometrisk formel for å beregne høyden på en skala trekant

Hvordan beregne sidene?

Når du har mål på to sider og vinkelen i motsetning til disse, er det mulig å bestemme den tredje siden som bruker Cosenos teorem.

For eksempel, i en AB -trekant, trekkes høyden i forhold til AC -segmentet. På denne måten er trekanten delt inn i to rektangeltrekanter.

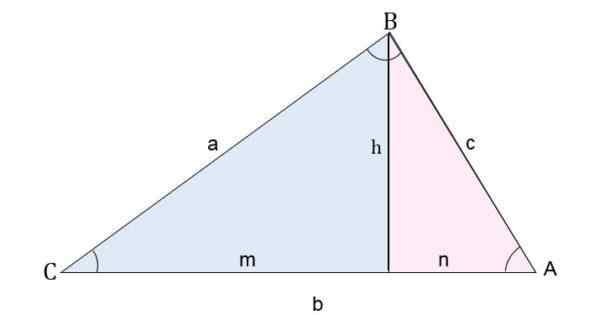Deling av en skalen trekant i to rektangler for å beregne sidene

For å beregne side C (segment AB), brukes Pythagoras teorem for hver trekant:

• For den blå trekanten må du:

c² = h² + m²

Som m = b - n, erstattes den:

c² = h² + b² (B - N)²

c² = h² + b² - 2bn + N².

• For den rosa trekanten må du:

h² = a² - n²

Den erstattes i forrige ligning:

c² = a² - n² + b² - 2bn + N²

c² = a² + b² - 2bn.

Å vite at n = a _* Cos C, erstattes i den forrige ligningen og verdien av side C oppnås:

c² = a² + b² - 2b_* til _* cos c.

Ved loven fra Cosenos kan sidene beregnes som:

• til² = b² + c² - 2b_* c _* ting.
• b² = a² + c² - 2_* c _* cos b.
• c² = a² + b² - 2b_* til _* cos c.

Det er tilfeller der tiltakene på trekantesidene ikke er kjent, men høyden og vinklene som dannes i toppunktene. For å bestemme området i disse tilfellene er det nødvendig å anvende trigonometriske grunner.

Å kjenne vinkelen til en av dens hjørner, er kategorien identifisert og den tilsvarende trigonometriske grunnen brukes:

Trigonometrisk formel for å beregne sidene av en skalen trekant

For eksempel vil kateto ab være motsatt for vinkel C, men ved siden av vinkelen a. Avhengig av siden eller benet som tilsvarer høyden, blir den andre siden ryddet for å oppnå verdien av dette.

Løste øvelser

Første trening

Beregn området og en høyde på Escalano ABC -trekanten, vel vitende om at sidene er:

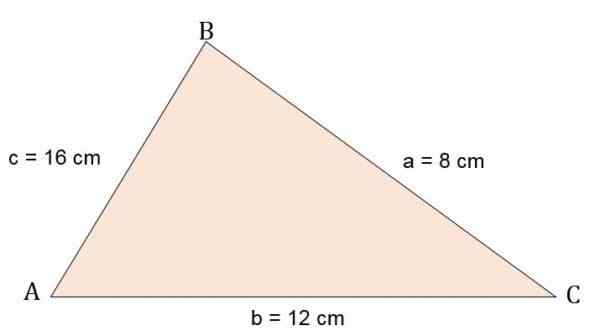
A = 8 cm.

B = 12 cm.

C = 16 cm.

Løsning

Ettersom data blir gitt tiltakene på de tre sidene av Scalene Triangle.

Fordi du ikke har verdien av høyden, kan området bestemmes ved å bruke Herón -formelen.

Først beregnes semi -perimeteret:

sp = (a + b + c) ÷ 2

sp = (8 cm + 12 cm + 16 cm) ÷ 2

sp = 36 cm ÷ 2

sp = 18 cm.

Nå erstattes verdiene i Heróns formel:

Kan tjene deg: Absolutt frekvens: Formel, beregning, distribusjon, eksempel Herón Formula

Å vite at området kan beregnes den relative høyden til side B. Fra den generelle formelen, rydde den du har:

Område = (side _* H) ÷ 2

46, 47 cm² = (12 cm _* H) ÷ 2

H = (2 _* 46,47 cm²) ÷ 12 cm

H = 92,94 cm² ÷ 12 cm

H = 7,75 cm.

Andre trening

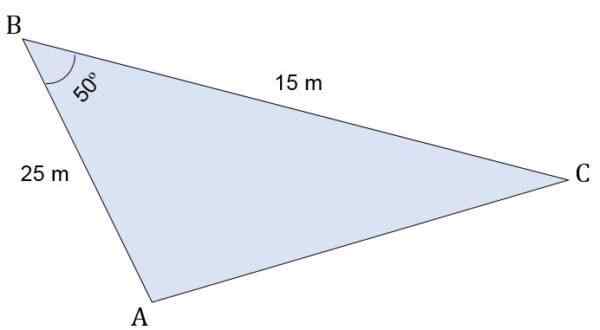
Gitt ABC Escalano Triangle, hvis tiltak er:

• Segment ab = 25 m.
• Segment bc = 15 m.

I toppunkt B dannes en vinkel på 50º. Beregn høyden i forhold til side C, omkretsen og området til den trekanten.

Løsning

I dette tilfellet er det to -sider tiltak. For å bestemme høyden er det nødvendig å beregne målet på tredje side.

Ettersom den motsatte vinkelen gis til de gitte sidene, er det mulig å anvende loven til Cosenos for å bestemme målet på AC (B) -siden:

b² = a² + c² - 2_*c _* cos b

Hvor:

A = bc = 15 m.

C = ab = 25 m.

B = AC.

B = 50^enten.

Dataene erstattes:

b² = (15)² + (25)² - 2_*(femten)_*(25) _* cos 50

b² = (225) + (625) - (750) _* 0.6427

b² = (225) + (625) - (482,025)

b² = 367.985

B = √367,985

B = 19,18 m.

Ettersom du allerede har verdien av de tre sidene, beregnes omkretsen av den trekanten:

P = side til + side b + side c

P = 15 m + 25 m + 19, 18 m

P = 59,18 m

Det er nå mulig å bestemme området ved å bruke Herón -formelen, men først må semi -perimeteret beregnes:

sp = p ÷ 2

sp = 59,18 m ÷ 2

sp = 29,59 m.

Sidens mål og semi -perimeter i Herón -formelen erstattes:

Til slutt, når du kjenner til området, kan den relative høyden beregnes til side C. Fra den generelle formelen, og rydder den, må du:

Område = (side _* H) ÷ 2

143,63 m² = (25 m _* H) ÷ 2

H = (2 _* 143,63 m²) ÷ 25 m

H = 287,3 m² ÷ 25 m

H = 11,5 m.

Tredje øvelse

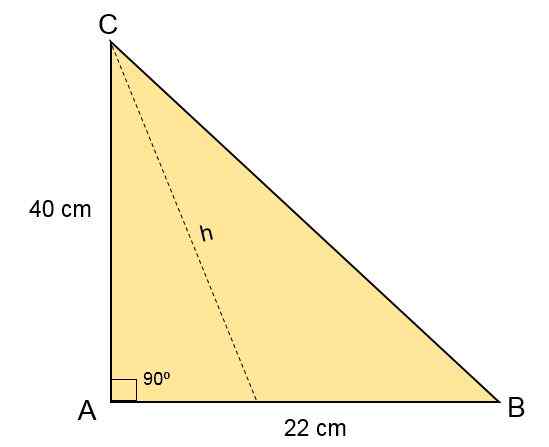
I Escaleno ABC -trekanten måler B -siden 40 cm, C -siden måler 22 cm, og i toppunktet er A en vinkel på 90^enten. Beregn området til den trekanten.

Løsning

I dette tilfellet er det gitt tiltakene på to sider av ABC -skala -trekanten, så vel som vinkelen som dannes i toppunktet til.

For å bestemme området er det ikke nødvendig å beregne målet på side A, siden gjennom trigonometriske grunner er vinkelen brukt til å finne den.

Ettersom den motsatte vinkelen er kjent for høyden, vil dette bli bestemt av produktet på den ene siden og brystets bryst.

Erstatter i områdeformelen du må:

• Område = (side _* H) ÷ 2
• H = c _* sin a

Område = (B _* c _* sin a) ÷ 2

Område = (40 cm _* 22 cm _* Sen 90) ÷ 2

Område = (40 cm _* 22 cm _* 1) ÷ 2

Område = 880 cm² ÷ 2

Område = 440 cm².

Referanser

1. Álvaro Rendón, til. R. (2004). Teknisk tegning: Aktivitetsnotatbok.
2. Ángel Ruiz, h. B. (2006). Geometrier. Cr teknologisk, .
3. Angel, a. R. (2007). Elementær algebra. Pearson Education,.
4. Baldor, a. (1941). Algebra. Havana: kultur.
5. Barbosa, J. L. (2006). Flat euklidisk geometri. Rio de Janeiro,.
6. Coxeter, h. (1971). Grunnleggende om geometri. Mexico: Limusa-Wiley.
7. Daniel c. Alexander, g. M. (2014). Elementær geometri for studenter. Cengage Learning.
8. Harpe, p. d. (2000). Temaer i geometrisk gruppeteori. University of Chicago Press.