Samtidig vektoregenskaper, eksempler og øvelser

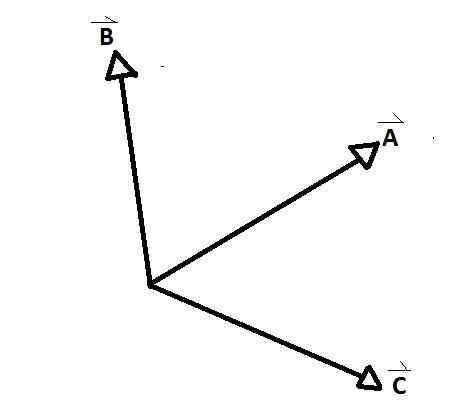
De Samtidig vektorer De er gruppene av vektorer hvis akser sammenfaller på et tidspunkt, og dannes mellom hvert par av dem en indre og en ytre vinkel. Et klart eksempel observeres i det nedre figuret, hvor A, B og C er samtidig vektorer med hverandre.

D og E i motsetning til resten er det ikke. Det er vinkler dannet mellom samtidige vektorer AB, AC og CB. Forholdsvinkler mellom vektorer kalles.

[TOC]

Kjennetegn

-De har et felles punkt, som sammenfaller med deres opprinnelse: alle størrelsene på de samtidige vektorene starter fra et felles punkt til deres respektive ytterpunkter.

-Opprinnelsen regnes som vektorhandlingspunktet: et handlingspunkt må etableres som vil bli direkte påvirket av hver av de samtidige vektorene.

-Domenet ditt i flyet og rommet er R² og r³ henholdsvis: Samtidig vektorer står fritt til å dekke hele det geometriske rommet.

-Tillater forskjellige notasjoner i samme gruppe vektorer. I henhold til grenene til studien er forskjellige notasjoner til stede i operasjoner med vektorer.

Typer vektorer

Grenen av vektorene har flere underavdelinger, blant noen kan de utnevnes: parallell, vinkelrett, koplanarios, tilsvarende, motsatt og enhetlig. Samtidige vektorer vises på denne listen, og som alle de tidligere utnevnte, har de mange applikasjoner i forskjellige vitenskaper.

De er veldig vanlige i vektorstudien, fordi de representerer en lønnsom generalisering i operasjonene med dem. Både i planet og i verdensrommet er samtidig vektorer for aktuell bruk for representasjon av forskjellige elementer og studerer deres innflytelse på et bestemt system.

Vektornotasjon

Det er forskjellige måter å representere et vektorelement. Det viktigste og mest kjente er:

Kartesisk

Foreslått ved denne samme matematiske tilnærmingen, betegner vektorer med en liste som tilsvarer størrelsene på hver akse (x, y, z)

A: (1, 1, -1) Space A: (1, 1) Plan

Polar

De tjener bare til å betegne vektorer i planet, selv om dybdekomponenten i den integrerte beregningen er tildelt. Den består med en lineær størrelse r og en vinkel med hensyn til polaraksen Ɵ.

Kan tjene deg: Inferensiell statistikk: Historie, egenskaper, hva er det for, eksempler

A: (3, 45⁰ ) Plan A: (2, 45⁰ , 3) Plass

Analytisk

Definere størrelsen på vektoren gjennom versorene. Versorene (R&E + K) representerer enhetsvektorene som tilsvarer aksene X, y og

A: 3I + 2J - 3K

Sfærisk

De ligner på polar notasjon, men med tilsetning av en andre vinkel som feier på flyet Xy symbolisert av Δ.

A: (4, 60^enten , π/4)

Operasjoner med samtidig vektorer

Samtidige vektorer brukes mest til å definere operasjoner mellom vektorer, fordi det er lettere å sammenligne elementene i vektorene når de oppstår på en samtidig måte.

Sum (a + b)

Summen av samtidige vektorer tar sikte på å finne den resulterende vektoren V_r. Som ifølge grenen av studien tilsvarer en endelig handling

For eksempel: 3 strenger er bundet a, b, c til en boks, hver ende av tauet er i hendene på et emne. Hvert av de 3 forsøkspersonene må trekke tauet i en annen retning enn de andre 2.

A: (AX, AY, AZ) B: (BX, BY, BZ) C: (CX, CY, CZ)

A+b+c = (ax+bx+cx; ay+av+cy; az+bz+cz) = V_r

Boksen kan bare bevege seg i en retning, derfor V_r vil indikere retningen og følelsen av forskyvningen av boksen.

Forskjell (A - B)

Det er mange kriterier angående forskjellen mellom vektorer, mange forfattere velger å ekskludere det og hevder at bare summen mellom vektorer er fastsatt, hvor forskjellen er summen av den motsatte vektoren. Sannheten er at algebraisk vektorer kan trekkes fra.

A: (Ax, AY, AZ) B: (BX, BY, BZ)

A-b = a + (-b) = (ax-bx; ay-be; az-bz) = [ax + (-bx); ay + (-by); AZ + (-bz)]

Scalar Product (a . B)

Også kjent som Punto -produktet, genererer en skalærverdi som kan relateres til flere størrelser i henhold til studiegrenen.

For geometri indikerer parallellogramområdet dannet av paret av samtidige vektorer gjennom parallellogrammetoden. For mekanisk fysikk definerer arbeidet som er utført av en styrke F Ved å bevege en kropp en avstand ΔR.

Det kan tjene deg: sammensatt proporsjonalitet: forklaring, tre sammensatte regel, øvelser

ѡ = f . ΔR

Som navnet tilsier, genererer det en skalarverdi og er definert som følger:

Være vektorene a og b

A: (Ax, AY, AZ) B: (BX, BY, BZ)

-Analytisk form:

( TIL . B) = | a |.| B |.Cos θ

Hvor θ er den indre vinkelen mellom begge vektorene

-Algebraisk form:

( TIL . B) = (øks.Bx + ay.av + az.Bz)

Vektorprodukt (a x b)

Vektoren eller punktproduktet mellom to vektorer, definerer en tredje vektor C som har kvaliteten på å være vinkelrett på B og C. I fysikk definerer vektormomentet τ Baseelement i rotasjonsdynamikk.

-Analytisk form:

| A X B | = | A |.| B |.Sin θ

-Algebraisk form:

(A X B) = = (Øks . av - ay . bx)- (øks . BZ - AZ . bx) J + (Øks . av - ay . bx) k

-Relativ bevegelse: r_A/b

Grunnlaget for relativitet er den relative bevegelsen og de samtidige vektorene er grunnlaget for den relative bevegelsen. Du kan utlede posisjoner, hastigheter og relative akselerasjoner ved å bruke følgende ideer for ideer.

r _A/b = r_TIL - r_B    ; Relativ stilling angående B

v _A/b = v_TIL - v_B  ; Relativ hastighet på respekten til B

til _A/b = a_TIL - til_B  ; Relativ akselerasjon av respekt til B

Eksempler: Løste øvelser

Oppgave 1

La A, B og C samtidig vektorer.

A = (-1, 3, 5) b = (3, 5, -2) c = (-4, -2, 1)

-Definer den resulterende vektoren V_r = 2A - 3B + C

2a = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)

-3b = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)

V_r = 2a + (-3b) + c = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)

V_r = ([-2+(-9)+(-4)]; [6+(-15)+(-2)]; (10+6+1))

V_r = (-15, -11, 17)

-Definere skalarproduktet (a . C)

( TIL . C) = (-1, 3, 5) . (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4 -6 + 5

( TIL . C) = 3

-Beregn vinkelen mellom A og C

( TIL . C) = | a |.| C |.Cos θ hvor θ er den korteste vinkelen mellom vektorer

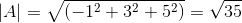
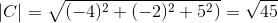
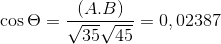
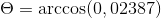
θ = 88.63⁰

 -Finn en vektor vinkelrett på A og B

For dette er det nødvendig å definere vektorproduktet mellom (-1, 3, 5) og (3, 5, -2). Som forklart før, bygges en 3 x 3 -matrise der den første raden er sammensatt av listen over enhetsvektorer (i, j, k). Deretter består 2. og 3. rad av vektorene som skal betjenes, og respekterer den operasjonelle ordren.

Kan tjene deg: desimalnotasjon

(A X B) = = [(-1) . 5 - (3 . 3)] Yo  - [ (-1) . (-2) - (5 . 3)] J + [ (-1) . 5 - (3 . 3)] k

(A X B) = (-5 - 9) Yo - (2 - 15) J + (-5 - 9) k         

(A X B) =  -14 I + 13 J - 14 K

Oppgave 2 

La v_til og v_b Hastighetsvektorene til henholdsvis A og B. Beregn B -hastigheten fra a.

V_til = (3, -1, 5) V_b = (2, 5, -3)

I dette tilfellet blir den relative hastigheten til B bedt om fra V_B/a

V_B/a = V_B - V_TIL

V_B/a = (2, 5, -3) -(3, -1, 5) = (-1, 6, -8)

Dette er Veloc -vektoren til B sett fra en. Der en ny vektor av B -hastigheten er beskrevet ved referanse til en observatør plassert i A og beveger seg med hastigheten på en.

Foreslåtte øvelser

1-konstruksjon 3 vektorer A, B og C som er samtidig og relaterer 3 operasjoner mellom dem gjennom en praktisk øvelse.

2 -vektorer A: (-2, 4, -11), B: (1, -6, 9) og C: (-2, -1, 10). Finn vinkelrett vektorer til: a og b, c og b, sum a + b + c.

4-bestemmende 3 vektorer som er vinkelrett på hverandre, uten å ta hensyn til koordinataksene.

5-definer arbeidet utført av en styrke som løfter en 5 kg masseblokk, fra bunnen av en 20 m dyp brønn.

6-Swamker algebraic at subtraksjon av vektorer er lik summen av den motsatte vektoren. Rettferdiggjøre postulatene dine.

7-denote en vektor i alle notasjoner utviklet i denne artikkelen. (Cartesian, Polar, Analytics og sfærisk).

8-Magnetiske krefter som utøves på en magnet som hviler på et bord, er gitt av følgende vektorer; V: (5, 3, -2), T: (4, 7, 9), H: (-3, 5, -4). Bestem i hvilken retning magneten vil bevege seg hvis alle magnetiske krefter fungerer samtidig.

Referanser

1. Euklidisk geometri og transformasjoner. Clayton w. dukke. Couer Corporation, 1. januar. 2004
2. Hvordan løse Bruk matematikkproblemer l. Moiseiwitsch. Couer Corporation, 10. april. 2013
3. Grunnleggende konsepter av geometri. Walter Prenowz, Meyer Jordan. Rowman & Littlefield, 4. oktober. 2012
4. Vektorene. Rocío Navarro Lacoba, 7. juni. 2014
5. Lineær algebra. Bernard Kolman, David R. HØYDE. Pearson Education, 2006