Areolar hastighet hvordan det beregnes og løses øvelser

De Areolar hastighet Det er det feiende området per tidsenhet og er konstant. Det er typisk for hver planet og oppstår fra beskrivelsen av Keplers andre lov på matematisk måte. I denne artikkelen vil vi forklare hva den består av og hvordan den beregnes.

Bommen som representerer oppdagelsen av planeter utenfor solsystemet har reaktivert interessen for planetariske bevegelser. Ingenting mener at disse ekso-planettene følger andre lover enn de som allerede er kjent og gyldige for solsystemet: Keplers lover.

Johannes Kepler var astronomen som uten hjelp av teleskopet og brukte observasjonene fra sin mentor Tycho Brahe, skapte en matematisk modell som beskriver bevegelsen til planetene rundt solen.

Han forlot denne modellen uttrykt i de tre lovene som bærer navnet hans, og som forblir like gyldige i dag som i 1609, da han etablerte de to første og 1618, dato den tredje.

[TOC]

Kepler lover

På nåværende språk sier Keplers tre lover som dette:

1. Banene til alle planetene er elliptiske og solen er i fokus.

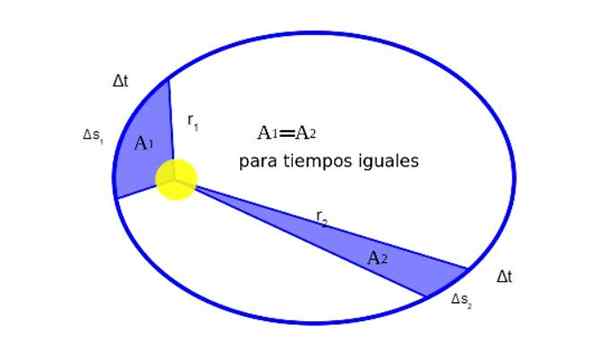
2. Posisjonsvektoren som går fra solen til en planet feier like områder i like tider.

3. Torget i orbitalperioden til en planet er proporsjonal med kuben til semi-Weise of the Ellipse beskrevet.

En planet vil ha en lineær hastighet, som ethvert kjent objekt som beveger seg. Og det er mer: Når du skriver Keplers andre lov i matematisk form, oppstår et nytt konsept kalt areolar hastighet, typisk for hver planet oppstår.

Hvorfor beveger planeter elliptisk rundt solen?

Jorden og de andre planetene beveger seg rundt solen takket være det faktum at den utøver en styrke på dem: gravitasjonsattraksjonen. Det samme gjelder enhver annen stjerne og planetene som samsvarer med systemet ditt, hvis du har dem.

Det kan tjene deg: sensitiv varme: konsept, formler og øvelser løst

Dette er en styrke av den typen som er kjent som sentral kraft. Vekten er en sentral kraft som alle er kjent med. Objektet som utøver den sentrale kraften, det være seg solen eller en fjern stjerne, tiltrekker planetene mot sitt sentrum, og de beveger seg og beskriver en lukket kurve.

I prinsippet kan denne kurven tilnærmes som en omkrets, da Nicolás Copernico, en polsk astronomskaper av den heliosentriske teorien, gjorde.

Ansvarlig styrke er gravitasjonsattraksjon. Denne styrken avhenger direkte av massene til stjernen og den aktuelle planeten og er omvendt proporsjonal med kvadratet på avstanden som skiller dem.

Problemet er ikke så enkelt, for i et solsystem samhandler alle elementer på denne måten, og legger til kompleksitet til saken. De er heller ikke partikler, ettersom stjerner og planeter er målbar størrelse.

Av denne grunn er det sentrale punktet i bane eller krets som er reist av planetene ikke akkurat sentrert på stjernen, men på et punkt kjent som tyngdepunktet i sol-planet-systemet.

Den resulterende bane er elliptisk. Følgende bilde viser det, og tar som et eksempel jorden og solen:

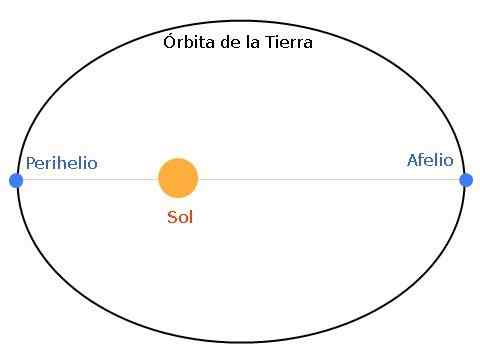Figur 1. Jordens bane er elliptisk, med solen lokalisert i en av fokusene. Når jorden og solen er i sin maksimale avstand, sies det at jorden er i afelium. Og hvis avstanden er minimal, snakker vi om perihelio.

Apeliet er den fjerneste posisjonen fra jorden til solen, mens perihelium er det nærmeste punktet. Ellipsen kan være mer eller mindre flatet, i henhold til egenskapene til stjernersystemet - planeten.

Asels og perihelio -verdiene varierer årlig, siden de andre planetene forårsaker forstyrrelser. For andre planeter kalles disse stillingene henholdsvis støtte og kompetanse.

Størrelsen på den lineære hastigheten til en planet er ikke konstant

Kepler oppdaget at når en planet går i bane rundt solen, under sin Barr -bevegelse like områder i like tider. Figur 2 viser grafisk betydningen av dette:

Det kan tjene deg: Hva er balansen i partikkelen? (Med eksempler)Figur 2. Posisjonsvektoren til en planet med hensyn til solen er r. Når planeten beskriver sin bane, reiser en ellipsebue ΔS i en tid Δt.

Matematisk, det faktum at₁ være lik₂ Det kommer til uttrykk slik:

Bueskantene er små, slik at hvert område kan nærme seg det for en trekant:

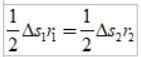
Som ΔS =vΔt, Der V er planetens lineære hastighet på et gitt punkt, når vi erstatter har vi:

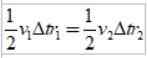
Og siden tidsintervallet Δt er det samme, oppnås det:

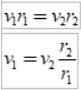
Som r₂ > r₁, da v₁ > v₂, Med andre ord, den lineære hastigheten til en planet er ikke konstant. Faktisk går jorden raskere når den er i perihelium enn når den er i afelium.

Derfor er jordens lineære hastighet eller en hvilken som helst planet rundt solen ikke en styrke som tjener til å karakterisere bevegelsen til nevnte planet.

Areolar hastighet

Keplers andre lov antyder en ny størrelse kalt areolar hastighet. Det er definert som området feid per tidsenhet og er konstant. For å beregne den, brukes følgende figur:

Figur 3. Jordens posisjonsvektor (eller planet) med hensyn til sol.

Et lite område feid av jorden velges mens vi utfører sin elliptiske krets, som vi vil betegne hvordan ΔA. Tiden som trengs for dette er Δt.

Figur 3 viser jordens posisjonsvektor med hensyn til solen, betegnet med r. Når jorden beveger seg, opplever du en forskyvning ΔR.

Dette området tilsvarer halvparten av rektangelområdet vist i figur 3:

Kvotienten ΔR/ΔT er nettopp jordens lineære hastighet, så den areolære hastigheten gjenstår:

V_TIL I det internasjonale systemet er de:

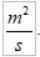
Merk at mens både R og V varierer, forblir produktet konstant. Dette gjør areolar hastighet til en veldig passende størrelse for å karakterisere bevegelsen til en planet rundt stjernen.

Kan tjene deg: Antoinkonstanter: Formler, ligninger, eksempler

Produktet av R og V er størrelsen på vinkelmomentet L, slik at den areolære hastigheten kan uttrykkes som:

Beregning av lineær hastighet og areolar hastighet

Med følgende eksempel vil vi vise hvordan du beregner den areolære hastigheten når noen parametere for planetariske bevegelser er kjent:

Trening

En ekso-planet beveger seg rundt solen etter en elliptisk bane, i henhold til Keplers lover. Når det er i eksperiment, er radiovektoren r₁ = 4 · 10⁷ km, og når det er i støtten er r₂ = 15 · 10⁷ km. Den lineære hastigheten i sin kompetanse er v₁ = 1000 km/s.

Regne ut:

A) Størrelsen på hastigheten i støtten.

B) Exo-planetens areolar hastighet.

C) Lengden på ellipsen Major Semi -Axis.

Svar til)

Ligningen brukes:

der numeriske verdier erstattes.

Hvert begrep identifiseres som følger:

v₁ = Hastighet i støtte; v₂ = Hastighet i eksperten; r₁= Forfatteravstand,

r₂= Avstand fra eksperten.

Med disse verdiene er det oppnådd:

Svar b)

Ligningen som skal brukes er

der par verdiene r og v av eksperiment eller støtten kan erstattes, siden v_TIL Det er en planet konstant:

Svar C)

Lengden på ellipsenes viktigste semi -aksel er semi -semi -semi -semi -semi -seismum og ekspertisen:

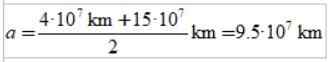
Bibliografi

1. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. Mexico. Cengage Learning Editors. 367-372.
2. Stern, d. (2005). De tre Kepler -lovene i planetarbevegelsen. Hentet fra PWG.GSFC.gryte.Gov
3. Merk: Den foreslåtte øvelsen ble tatt og endret fra følgende tekst i en McGrawhill -bok. Dessverre er det et isolert kapittel i PDF -format, uten tittelen eller forfatteren: MHEducation.ES/BCV/GUIDE/KAPITTEL/844817027X.PDF