Gjennomsnittlig hastighetsformler, hvordan den beregnes og løses trening

De gjennomsnittshastighet For en mobilpartikkel er det definert som årsaken mellom variasjonen av posisjonen hun opplever og tidsintervallet som brukes i endringen. Den enkleste situasjonen er en der partikkelen beveger seg langs en rett linje representert av X -aksen.

Anta at det mobile objektet inntar X -stillingene₁ og x₂ I tider t₁ og T₂ henholdsvis. Definisjonen av gjennomsnittshastighet v_m Det er matematisk representert som følger:

Enhetene til v_m I det internasjonale systemet er de meter/sekund (m/s). Andre vanlige bruksenheter som vises i mobile tekster og enheter er: km/t, cm/s, miles/t, føtter/s og mer, forutsatt at de er lengden/tidsformen.

Den greske bokstaven "Δ" lyder "Delta" og brukes til å oppsummere forskjellen mellom to mengder.

[TOC]

Kjennetegn på gjennomsnittlig hastighetsvektor V_m

Gjennomsnittshastigheten er et viktig kjennetegn ved bevegelse. Kilde: Pixabay

Gjennomsnittshastigheten er en vektor, siden den er relatert til posisjonsendringen, som igjen er kjent som Vektorforskyvning.

Denne kvaliteten er representert med fet skrift eller av en pil over brevet som utpeker størrelsesorden. Imidlertid, i en dimensjon, er den eneste mulige retningen av x -aksen og kan derfor dispenseres med vektortrollen.

Siden vektorene har størrelse, retning og mening, indikerer et første blikk på ligningen at gjennomsnittshastigheten vil ha samme retning og følelse som forskyvningen.

Se for deg partikkelen til eksemplet som beveger seg langs en rett linje. For å beskrive bevegelsen din, er det nødvendig å indikere et referansepunkt, som vil være "opprinnelsen" og vil bli betegnet som eller.

Partikkelen kan bevege seg bort eller nærme seg eller, enten til venstre eller til høyre. Du kan også bruke mye eller lite tid til å nå en bestemt stilling.

Det kan tjene deg: Varme: Formler og enheter, egenskaper, hvordan det måles, eksempler

Størrelsene som er blitt nevnt: posisjon, forskyvning, intervall av tid og gjennomsnittshastighet, beskriv partikkelenes oppførsel mens du beveger seg. Det handler om størrelsesorden Kinematisk.

For å skille posisjonene eller plasseringene til venstre for eller tegnet (-) brukes og de som finnes til høyre for eller bære skiltet (+).

Gjennomsnittshastigheten har en geometrisk tolkning som kan sees i følgende figur. Det er skråningen på linjen som passerer gjennom P- og Q -punktene. Når du skjærer til stillingen vs posisjon. tid på to punkter, det er en linje Tørking.

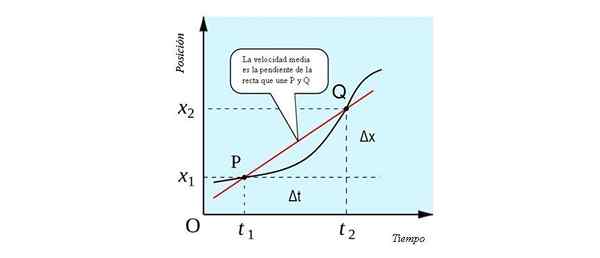Geometrisk tolkning av gjennomsnittshastighet, som en skråning av linjen som blir med P- og Q -punktene. Kilde: すじにく シチュー [CC0].

Tegnene på gjennomsnittshastighet

For følgende analyse må det tas i betraktning at t₂ > t₁. Det vil si at det følgende øyeblikket alltid er større enn strømmen. Denne måten t₂ - t₁ Det er alltid positivt, noe som vanligvis gir mening daglig.

Da blir tegnet på gjennomsnittshastigheten bestemt av x₂ - x₁. Legg merke til at det er viktig.

Eller "frem" eller "tilbake", som leseren foretrekker.

Hvis gjennomsnittshastigheten er positiv, betyr det det gjennomsnittlig verdien av "x”Øker over tid, selv om dette ikke betyr at det kunne ha gått ned på et tidspunkt i den vurderte tiden - Δt -.

Imidlertid i globale termer, på slutten av tiden Δt, Hun endte med en større posisjon enn den hun hadde i begynnelsen. Detaljene i bevegelsen blir ignorert i denne analysen.

Du kan tjene deg: Newtons tredje lov: Søknader, eksperimenter og øvelser

Hva om gjennomsnittshastigheten er negativ? Vel, det betyr at partikkelen ender med en mindre koordinat enn den den begynte. Groso -modus beveget seg bakover. La oss se på noen numeriske eksempler:

Eksempel 1: Gitt de innledende og endelige posisjonene som er angitt, angir tegnet på gjennomsnittshastigheten. Hvor beveget partikkelen seg globalt?

a) x₁ = 3 m; x₂ = 8 m

Svar: x₂- x₁  = 8 m - 3 m = 5 m. Positiv gjennomsnittshastighet, partikkelen beveget seg fremover.

b) x₁ = 2 m; x₂ = -3 m

Svar: x₂ - x₁ = -3 m -2 m = -5 m. Gjennomsnittlig negativ hastighet, partikkelen beveget seg bakover.

 c) x₁  = - 5 m; x₂ = -12 m

Svar: x₂ - x₁   = -12 m -( -5 m) = -7 m. Gjennomsnittlig negativ hastighet, partikkelen beveget seg bakover.

d) x₁  = - 4 m; x₂ = 10 m

Svar: x₂ - x₁  = 10 m - (-4m) = 14 m. Positiv gjennomsnittshastighet, partikkelen beveget seg fremover.

Kan gjennomsnittshastigheten være 0? Ja. Så lenge utgangspunktet og ankomstpunktet er det samme. Betyr dette at partikkelen nødvendigvis var i ro hele tiden?

Nei, det betyr bare at turen var tur / retur. Kanskje han reiste raskt eller kanskje veldig sakte. For nå er det ikke kjent.

Gjennomsnittshastigheten: en skalær størrelse

Dette fører til at vi definerer et nytt begrep: Gjennomsnittshastighet. I fysikk er det viktig å skille mellom vektorstørrelsene og størrelsene som ikke er: skalarene.

For partikkelen som gjorde tur / retur, er gjennomsnittshastigheten 0, men den kunne ha vært veldig rask eller kanskje ikke. For å vite det, er gjennomsnittshastigheten definert som:

Enhetene for gjennomsnittshastigheten er de samme som for gjennomsnittshastigheten. Den grunnleggende forskjellen mellom begge størrelsene er at gjennomsnittshastigheten inkluderer interessant informasjon om retningen og retningen på partikkelen.

Det kan tjene deg: Fermionic Condensate: Egenskaper, applikasjoner og eksempler

På den annen side gir gjennomsnittshastigheten bare numerisk informasjon. Med henne er det kjent hvor raskt eller sakte partikkelen beveget seg, men ikke hvis han gjorde den fremover eller bakover. Det er derfor det er en skalær størrelse. Hvordan du kan skille dem for å betegne dem? En måte er å forlate fet skrift for vektorer, eller plassere en pil på dem.

Og det er viktig å merke seg at gjennomsnittshastigheten ikke trenger å være lik gjennomsnittshastigheten. For tur / retur er gjennomsnittshastigheten null, men gjennomsnittshastigheten gjør det ikke. Begge har samme numeriske verdi når de alltid reiser i samme retning.

Trening løst

Du skal hjem fra skolen stille på 95 km/t per 130 km. Begynn å regne og reduserer hastigheten til 65 km/t. Han kommer endelig hjem etter å ha kjørt i 3 timer og 20 minutter.

a) Hvor langt er skolen din hjem?

b) Hva var gjennomsnittshastigheten?

Svar:

a) Noen tidligere beregninger er nødvendige:

Turen er delt inn i to deler, den totale avstanden er:

D = d1+ d₂, Med d1 = 130 km

Den totale tiden er 3 timer og 20 minutter = 3 + 1/3 time = 10/3 timer = 3.33 timer (det er nødvendig å plassere de samme enhetene for tid, i dette tilfellet er det passende).

T2 = 3.33 - 1.37 timer = 1.96 timer

Beregning av d_2:

d₂ = 65 km/t x 1.96 H = 125. 4 km.

Skolen er D1+ D₂ = 255.4 km fra huset.

b) Nå kan du finne gjennomsnittshastigheten:

Referanser

1. Giancoli, d. Fysikk. Prinsipper med applikasjoner. Sjette utgave. Prentice Hall. 21-22.
2. Resnick, r. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Continental Editorial Company s.TIL. Av c.V. 20-21.
3. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7ma. Utgave. Mexico. Cengage Learning Editors. 21-23.