Relativ hastighetskonsept, eksempler, øvelser

De Relativ hastighet av et objekt er et som måles med hensyn til en gitt observatør, siden en annen observatør kan oppnå et annet tiltak. Hastigheten avhenger alltid av observatøren som måler den.

Derfor vil hastigheten til et objekt målt av en bestemt person være den relative hastigheten med hensyn til det. En annen observatør kan oppnå en annen verdi for hastigheten, fremdeles i tilfelle av samme objekt.

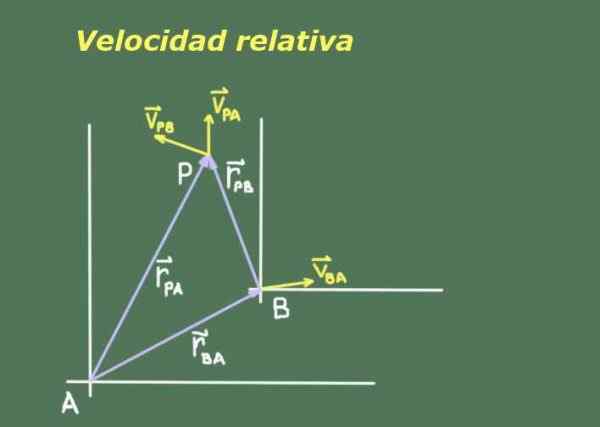
Figur 1. Skjema som representerer til punktet P i bevegelse, sett fra referansesystemer A og B. Kilde: Selvlaget.

Ettersom to observatører A og B som beveger seg fra hverandre, kan de ha forskjellige mål for et tredje P -objekt som beveger seg, er det nødvendig å se etter et forhold mellom posisjonene og hastighetene til P -visninger av A og B.

Figur 1 viser to observatører A og B med sine respektive referansesystemer, hvorfra de måler plasseringen og hastigheten til objekt P.

Hver observatør A og B måler plasseringen og hastigheten til objektet P på et bestemt tidspunkt t. I klassisk relativitet (eller galileisk) er tiden for observatør A den samme som for observatør B uavhengig av dens relative hastigheter.

Denne artikkelen handler om klassisk relativitet som er gyldig og anvendelig for de fleste hverdagssituasjoner der gjenstander har mye lavere hastighet enn lys.

Posisjonen til observatør B angående betegnelser som r_Ba. Ettersom posisjonen er en vektormengde bruker vi fet skrift for å indikere den. Posisjonen til objekt P med hensyn til en betegner som r_Pa og det av samme objekt P angående B r_Pb.

[TOC]

Forholdet mellom posisjoner og relative hastigheter

Det er et vektorforhold mellom disse tre stillingene som kan trekkes ut fra representasjonen av figur 1:

 r_Pa= r_Pb + r_Ba

Hvis det forrige uttrykket tas med hensyn til tiden t Vi vil oppnå forholdet mellom de relative hastighetene til hver observatør:

Du kan tjene deg: Newtons andre lov: søknader, eksperimenter og øvelser

V_Pa= V_Pb + V_Ba

I det forrige uttrykket er det den relative hastigheten til P med hensyn til en avhengig av den relative hastigheten til P med hensyn til B og den relative hastigheten til B med hensyn til.

Tilsvarende kan den relative hastigheten til P skrives med hensyn til den relative hastigheten til P med hensyn til A og den relative hastigheten til B.

V_Pb= V_Pa + V_AB

Det skal bemerkes at den relative hastigheten på med hensyn til B er lik og i strid med B med B med hensyn til A:

V_AB = -V_Ba 

Dette blir sett av et barn fra en bil i bevegelse

En bil går langs en rett vei, som går fra vest til dette, raskt fra 80 km/t mens i motsatt retning (og på den andre banen) kommer en motorsykkel raskt 100 km/t.

I baksetet på bilen reiser et barn som vil vite den relative hastigheten til en motorsykkel som nærmer seg ham. For å finne ut svaret, vil barnet bruke forholdene du nettopp har lest i forrige seksjon, og identifisere hvert koordinatsystem som følger:

-A er koordinatsystemet til en observatør på veien, og med hensyn til det er rapides av hvert kjøretøy målt.

-B er bilen og P vil være motorsykkelen.

Hvis du vil beregne hastigheten på moto p med hensyn til bil B, vil følgende forhold bli brukt:

V_Pb= V_Pa + V_AB=V_Pa - V_Ba

Tar som positiv den vest-østlige retningen du har:

V_Pb= (-100 km/t - 80 km/t) Yo = -180 km/t Yo

Dette resultatet tolkes som følger: motorsykkelen beveger seg med hensyn til bilen med en hastighet på 180 km/t og retning -Yo, det vil si dette til vest.

Det kan tjene deg: blokker algebra: elementer, eksempler, løste øvelser

Relativ hastighet mellom motorsykkelen og bilen

Motorsykkelen og bilen har krysset hver og en etter banen. Gutten som går i baksetet på bilen ser motorsykkelen bort og nå vil vite i hvilken hastighet han beveger seg bort fra ham, forutsatt at både motorsykkel og bil opprettholder de samme rapidene som før kryssing.

For å vite svaret, bruker barnet det samme forholdet som tidligere ble brukt:

V_Pb= V_Pa + V_AB=V _Pa - V_Ba

V_Pb= -100 km/t Yo - 80 km/t Yo = -180 km/t Yo

Og nå beveger motorsykkelen seg bort fra bilen med samme relative hastighet som de nærmet seg før de krysset.

Den samme motorsykkelen til del 2 returnerer ved å holde samme hastighet på 100 km/t, men endre adresse. Det vil si bilen (som fortsetter raskt 80 km/t) og motorsykkelen beveger seg begge i en positiv retning.

På et tidspunkt overstiger motorsykkelen bilen, og barnet som går i baksetet på bilen vil vite den relative hastigheten på motorsykkelen med hensyn til ham når han ser henne passere ved hennes side.

For å få svaret gjelder barnet igjen forholdene til den relative bevegelsen:

V_Pb= V_Pa + V_AB=V_Pa - V_Ba

V_Pb= +100 km/t Yo - 80 km/t Yo = 20 km/t Yo 

Barnet fra baksetet observerer motorsykkelen som fremmer bilen med en hastighet på 20 km/t.

-Trening løst

Oppgave 1

En motorbåt krysser en elv på 600 m bred og strømmer fra nord til sør. Hastigheten på elven er 3 m/s. Båthastigheten med hensyn til elvevannet er 4 m/s mot øst.

Kan tjene deg: grener av klassisk og moderne fysikk

(i) Finn båthastigheten med hensyn til elvebredden.

(ii) Angi hastigheten og retningen på båten med hensyn til land.

(iii) Beregn kryssetiden.

(iv) Hvor mye vil ha beveget seg sørover med hensyn til utgangspunktet.

Løsning 

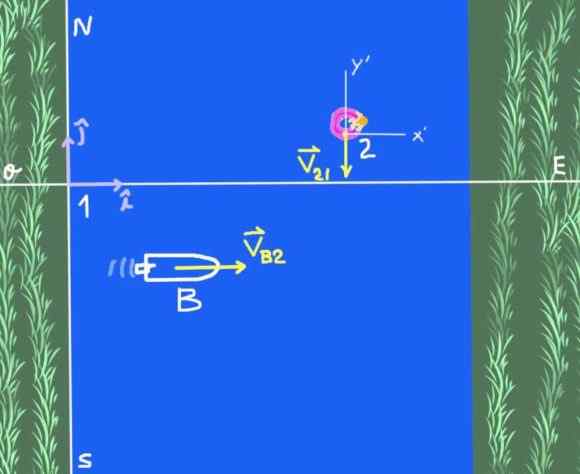Figur 2. Båt som krysser elven (øvelse 1). Kilde: Selvlaget.

Det er to referansesystemer: Solidaritetsreferansesystemet ved elvebredden som vi vil ringe 1 og referansesystemet 2 som er en observatør som flyter på elvevannet. Studiens objekt er båt B.

Hastigheten på båten med hensyn til elven er skrevet i en vektorform som følger:

VB2 = 4 Yo m/s

Hastigheten til observatør 2 (flåte over elven) med hensyn til observatør 1 (på land):

Vtjueen = -3 J m/s

Du vil finne båthastigheten med hensyn til land VB1.

VB1 = VB2 + Vtjueen

Svar i

VB1 = (4 Yo - 3 J) m/s   

Hastigheten på båten vil være den forrige hastighetsmodulen:

|VB1| = (42 + (-3) 2) ½ = 5 m/s

Svar ii

Og adressen vil være:

θ = Arcan (-¾) = -36,87º 

Svar iii

Båtenes kryssingstid er forholdet mellom elvenes bredde og komponenten X på båthastigheten med hensyn til jorden.

t = (600m)/(4 m/s) = 150 s 

Svar IV

For å beregne driften som båten hadde sør, multipliseres komponenten og hastigheten på båten med hensyn til bakken med kryssetiden:

d = -3 J m/s * 150 s = -450 J m

Forskyvningen mot sør med hensyn til utgangspunktet er 450m.

Referanser

1. Giancoli, d. Fysikk. Prinsipper med applikasjoner. 6. utgave. Prentice Hall. 80-90
2. Resnick, r. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Continental Editorial Company s.TIL. Av c.V. 100-120.
3. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Utgave. Mexico. Cengage Learning Editors. 95-100.
4. Wikipedia. Relativ hastighet. Gjenopprettet fra: Wikipedia.com
5. Wikipedia. Relativ hastighetsmetode. Gjenopprettet fra: Wikipedia.com