Ikke -coplanar vektors definisjon, forhold, øvelser

De Ikke -coplanares vektorer De er de som ikke deler det samme flyet. To gratis vektorer og ett punkt definerer et enkelt plan. En tredje vektor kan kanskje ikke dele det planet, og hvis det ikke gjør det, er dette ikke -koplanære vektorer.

Ikke -koblingsvektorer kan ikke representeres i to -dimensjonale rom, for eksempel et brett eller et ark, fordi noen av dem er inneholdt i den tredje dimensjonen. For å representere dem riktig, må du bruke perspektiv.

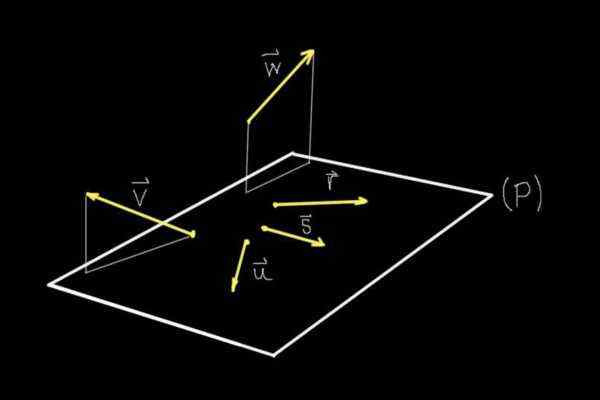Figur 1. Koplaner og ikke-koblingsvektorer. (Egen utdyping)

Hvis vi observerer figur 1, er alle objektene som er strengt vist i skjermen, men takket være perspektivet, er hjernen vår i stand til å forestille seg et plan (P) som kommer ut av det samme.

På det planet (p) er vektorene r, s, eller, mens vektorer v og W  De er ikke på det flyet.

Derfor vektorene r, s, eller De er Coplanarios eller Coplanares med hverandre siden de deler samme plan (P). Vektorene v og W De deler ikke en leilighet med noen av de andre vektorene som er vist, derfor er de ikke-kobling. 

[TOC]

Coplanares og Plane Likningsvektorer

Et fly er unikt definert hvis tre punkter er gitt i det tre -dimensjonale rommet.

Anta at de tre poengene er poenget TIL, punkt B Og poenget C som definerer flyet (P). Med disse punktene er det mulig å bygge to vektorer AB = U og AC = v som er ved konstruksjon med flyet (P).

Vektor (eller kryssprodukt) produkt av disse to vektorene resulterer i en tredje vinkelrett (eller normal) vektor for dem og derfor vinkelrett på planet (P):

n = u X v   => n ⊥ eller  og n ⊥ v   => n ⊥ (P)    

Kan tjene deg: vekt (fysisk): beregning, enheter, eksempler, øvelser

Ethvert annet punkt som tilhører flyet (P) må oppfylle den vektoren En q være vinkelrett på vektoren n; Dette tilsvarer å si at skalarproduktet (eller punktproduktet) av n med En q Det må være null:

n • En q = 0 (*)

Den forrige tilstanden tilsvarer å si det:

En q • (eller X v) = 0 

Denne ligningen sikrer at poenget Q tilhører flyet (P). 

Kartesiske ligning av flyet

Den forrige ligningen kan skrives på kartesisk måte. For dette skriver vi koordinatene til poengene TIL, Q og komponentene i den normale vektoren n:

A = (a, b, c)

Q = (x, y, z)

n= (NX, NY, NZ)

Slik at AQ -komponentene er:

En q= (X-A, Y-B, Z-C)

Tilstanden for vektoren En q være inneholdt i flyet (P) Det er tilstanden (*) som nå er skrevet slik:

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Beregning av punktproduktet gjenstår:

NX (X-A) + NY (Y-B) + NZ (Z-B) = 0

Hvis den utvikler og omorganiserer, gjenstår det:

nx x + ny y + nz z = nx a + ny b + nz c

Det forrige uttrykket er den kartesiske ligningen av et plan (P), avhengig av komponentene i en normal vektor til (P) og koordinatene til et punkt TIL som tilhører (P).

Betingelser for at tre vektorer skal være ikke -coplanes

Som tilstanden har blitt sett i forrige avsnitt En q • (eller X v) = 0 garanterer at vektoren En q Det er Coplanario A eller og v.

Hvis vi ringer W til vektoren En q Da kan vi bekrefte det:

W, eller og v De er koplaner, ja og bare hvis W • ( eller X v ) = 0.

Tilstand for ikke-atferd

Hvis det trippel (eller blandede produktet) produktet av tre vektorer er forskjellig fra null, er de tre vektorene ikke-omslag.

Det kan tjene deg: Politropisk prosess: Kjennetegn, applikasjoner og eksempler

Ja    W • ( eller X v ) ≠ 0 Da er U-, V- og W-vektorene ikke-koblanarios.

Hvis de kartesiske komponentene i U, V, V og W blir introdusert, kan ikke-atferdens tilstand skrives som følger:

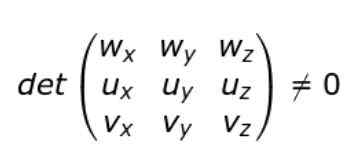Det vil si at hvis determinanten for matrisen (3 × 3) hvis rader er komponentene i U-, V- og W-vektorene, er vektorene ikke-kobling.

Trippelproduktet har en geometrisk tolkning og representerer volumet av parallellpiped generert av de tre ikke -coplanares -vektorene.

Figur 2. Tre ikke-koblingsvektorer definerer en parallellepipedo hvis volum er trippel produktmodulen. (Egen utdyping)

Årsaken er som følger; Når to av ikke-koblingsvektorene er multipliserer. 

Så når denne vektoren multipliseres. 

Med andre ord, du har parallellogramområdet generert av de to første multipliserte med høyden på den tredje vektoren.

Alternativ tilstand for ikke-kobling

Hvis du har tre vektorer og noen av dem ikke kan skrives som en lineær kombinasjon av de to andre, er de tre vektorene ikke-omslag. Det er tre vektorer eller, v og W De er ikke-omslag hvis tilstanden:

α eller + β v + γ W = 0

Det blir oppfylt bare når α = 0, β = 0 og γ = 0.

Løste øvelser

-Oppgave 1

Du har tre vektorer

eller = (-3, -6, 2);   v = (4, 1, 0) og W = (-1, 2, z)

Merk at vektorens z -komponent W Det er ukjent.

Finn verdiene som Z kan ta, slik at det er garantert at de tre vektorene ikke deler det samme planet.

Kan tjene deg: Stabil balanse: konsept og eksempler

Løsning 

Vi bruker igjen kriteriet for determinanten av matrisen som er dannet av rekkene til de tre vektorene, på denne måten forblir vi: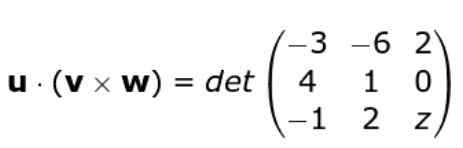Vi utvikler determinanten

W • ( eller X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3z + 24z + 18 = 21z + 18

Vi samsvarer med dette uttrykket med null verdi

21 z + 18 = 0

Og vi fjerner z

Z = -18/21 = -6/7

Hvis variabelen Z tok verdien -6/7, ville de tre vektorene være koplaner.

Slik at verdiene til z som garanterer at vektorene er ikke-omslag er de som er i følgende intervall:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Oppgave 2

Finn volumet av parallellpiped vist i følgende figur:

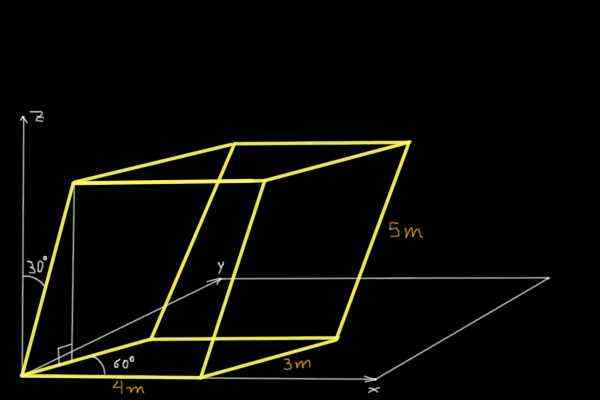
Løsning 

For å finne volumet av parallellpiped vist på figuren, vil de kartesiske komponentene til tre ikke-sammenslåtte ikke-koblingsvektorer bli bestemt i opprinnelsen til koordinatsystemet. Den første er vektoren eller  4m og parallelt med x -aksen:

eller= (4, 0, 0) m

Den andre er vektoren v I XY 3M -størrelsesplan som danner 60º med X -aksen:

v= (3*cos 60º, 3*sen 60º, 0) = (1.5, 2.6, 0.0) m

Og den tredje vektoren W av 5M og hvis projeksjon i XY -planet danner 60º med X -aksen, i tillegg W form 30º med Z -aksen.

W= (5*sin 30º*cos 60º, 5*sen 30º*sin 60º, 5*sen 30º)

Utført beregningene vi har: W= (1.25, 2.17, 2.5m.

Referanser

1. Figueroa, d. Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. 31-68.
2. Fysisk. Modul 8: Vektorer. Gjenopprettet fra: FRTL.Utn.Edu.ar
3. Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Editorial Company.28-66.
4. McLean, w. Schaum -serien. Mekanikk for ingeniører: statisk og dynamisk. 3. utgave. McGraw Hill. 1-15.
5. Wikipedia. Vektor. Gjenopprettet fra: det er.Wikipedia.org