Absorbans hva som er, eksempler og øvelser løst

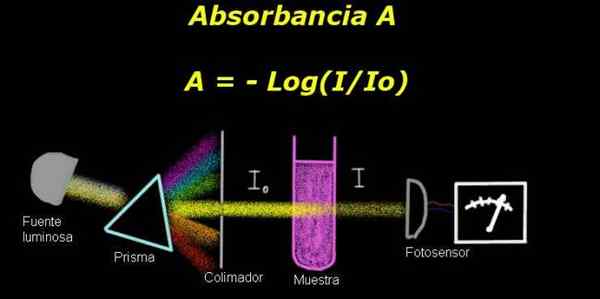
De absorbans Det er logaritmen med et negativt tegn på kvotienten mellom den nye lysintensiteten og lyshendelsesintensiteten på en prøve av gjennomskinnelig løsning som har blitt opplyst med monokromatisk lys. Denne kvotienten er overføring.

Den fysiske prosessen med passering av lys gjennom en prøve kalles lysende overføring, Og absorbans er et mål på det. Derfor blir absorbans den minst logaritmen for transmittans og er et viktig faktum for å bestemme konsentrasjonen av en prøve som vanligvis blir oppløst i et løsningsmiddel som vann, alkohol eller annen.

Figur 1. Skjema for absorbansprosessen. Utarbeidet av f. Zapata

For å måle absorbans er det nødvendig med en enhet Elektro-fotometer, som en strøm måles som er proporsjonal med den lysende intensitetshendelsen på overflaten.

Ved beregning av overføringen måles signalet om intensiteten som tilsvarer løsningsmidlet alene, og dette resultatet blir registrert som Io.

Deretter blir prøven oppløst i løsningsmidlet med de samme lysforholdene plassert. Tiltaket målt med elektrofotometeret er betegnet som Yo, som lar deg beregne transmittans T I henhold til følgende formel:

T = i / ienten

Det er en løsnet mengde. De Absorbans a Dette uttrykkes som:

A = - log (t) = - log (i / ienten)

[TOC]

Molar absorbanse og absorbasjon

Molekylene som utgjør et kjemikalie er i stand til å absorbere lys, og et mål på dette er nøyaktig absorbans. Det er resultatet av interaksjonen mellom fotoner og molekylære elektroner.

Derfor er det en størrelse som vil avhenge av tettheten eller konsentrasjonen av molekylene som utgjør prøven og også av den optiske banen eller avstanden som lyser av lyset. 

Du kan tjene deg: Newtons tredje lov: Søknader, eksperimenter og øvelser

Eksperimentelle data indikerer at absorbans TIL er lineært proporsjonal med konsentrasjonen C og avstand d Lys reiste. Så for å beregne den basert på disse parametrene, kan følgende formel etableres:

A = ε⋅C⋅d

I forrige formel, ε Det er en konstant av proporsjonalitet kjent under navnet til Molar absorberende.

Molar absorbitet avhenger av typen stoff og bølgelengde som absorbans måles. De Molar absorberende Det er også følsomt for temperaturen på prøven og pH av samme.

Beer-Lambert Law

Dette forholdet mellom absorbans, absorbitet, konsentrasjon og avstand fra tykkelsen på banen som lyset følger i prøven er kjent som øl-lambert lov.

Figur 2. Øllov - Lambert. Kilde: f. Zapata,

Nedenfor er det noen eksempler på hvordan du bruker det.

Eksempler

Eksempel 1

Under et eksperiment en prøve med rødt lys av en helium-neon laserlys, hvis bølgelengde er 633 nm. Et elektrofotometer måler 30 mV når laserlys påvirker direkte og 10 mV når det passerer gjennom en prøve. 

I dette tilfellet er overføringen:

T = i / io = 10 mV / 30 mV = ⅓.

Og absorbansen er:

A = - log (⅓) = log (3) = 0,48 

Eksempel 2

Hvis det samme stoffet er plassert i beholderen som har halvparten av det tykke.

Det må vurderes at hvis tykkelsen avtar til halvparten, synker absorbansen som er proporsjonal med den optiske tykkelsen med halvparten, det vil si A = 0,28. Tons transmittans vil bli gitt av følgende forhold:

Kan tjene deg: Vertikal skudd: Formler, ligninger, eksempler

T = 10-a = 10^(-0.28) = 0,53

Elektrofotometeret vil markere 0,53*30 mV = 15,74 mV.

Løste øvelser

Oppgave 1

Det er ønsket å bestemme den molare absorbiteten til en viss patentert forbindelse som er i løsning. For dette blir løsningen med lys fra en 589 nm natriumlampe opplyst. Prøven vil bli plassert på en 1,50 cm tykk.

Det er basert på en konsentrasjonsløsning 4,00 × 10^-4 føflekker per liter, og transmittansen måles, noe som resulterer i 0,06. Bestem med disse dataene den molære absorbiteten til prøven.

Løsning 

For det første bestemmes absorbans, som er definert som den minst logaritme basert ti av transmittans:

A = - log (t)

A = - log (0,06) = 1,22

Deretter brukes loven om Lambert-Beer som etablerer en sammenheng mellom absorbans, molar absorbasjon, konsentrasjon og optisk lengde:

A = ε⋅C⋅d

Rydding av den molare absorbiteten Følgende forhold oppnås:

ε = a/(c⋅d)

erstatte de gitte verdiene:

ε = 1,22/(4,00 × 10^-4 m⋅1,5 cm) = 2030 (m⋅cm)^-1

Det forrige resultatet er avrundet til tre viktige sifre.

Oppgave 2

For å forbedre nøyaktigheten og bestemme feilen i målet på molarabsorberingen av prøven i øvelse 1, blir prøven suksessivt fortynnet i halvparten av konsentrasjonen og overføringen måles i hvert tilfelle.

Fra CO = 4 × 10^-4 m med transmittans t = 0,06 Følgende datasekvens for transmittans og absorbans beregnet utover transmittansen oppnås:

CO/1-> 0,06-> 1,22

CO/2-> 0,25-> 0,60

CO/4-> 0,50-> 0,30

CO/8-> 0,71-> 0,15

CO/16-> 0,83-> 0,08

CO/32-> 0,93-> 0,03

CO/64-> 0,95-> 0,02

CO/128-> 0,98-> 0,01

CO/256-> 0,99-> 0,00

Med disse dataene, gjør:

Det kan tjene deg: Stasjonære bølger: Formler, egenskaper, typer, eksempler

a) En graf over absorbans basert på konsentrasjon.

b) En lineær justering av dataene og finn skråningen.

c) Fra den oppnådde skråningen, beregn molarabsorbasjonen.

Løsning 

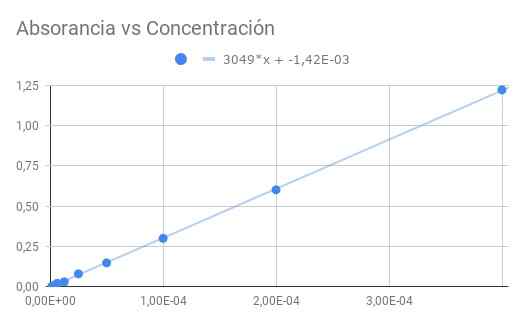Figur 3. Absorbans vs konsentrasjon. Kilde: f. Zapata.

Den oppnådde skråningen er produktet av molar absorganivitet ved den optiske avstanden, så deling av skråningen med lengde 1,5 cm får vi molar absorberende

ε = 3049/1,50 = 2033 (m⋅cm)^-1

Øvelse 3

Med dataene fra oppgave 2: 

a) Beregn absorganiviteten for hver data. 

b) Bestem en gjennomsnittsverdi for molar absorbitet, dens standardavvik og den statistiske feilen forbundet med gjennomsnittet.

Løsning 

Molar absorbering beregnes for hver av de testede konsentrasjonene. Husk at lysforhold og optisk avstand forblir faste.

Resultatene for molar absorbitet er:

2033, 2007, 2007, 1983, 2158, 1681, 2376, 1.872, 1862 i enheter på 1/(m*cm).

Fra disse resultatene kan vi ta gjennomsnittsverdien:

= 1998 (m*cm)^-1

Med et standardavvik på: 184 (m*cm)^-1

Gjennomsnittlig feil er standardavviket delt på kvadratroten til datanummeret, det vil si:

Δ = 184/9^0,5 = 60 (m*cm)^-1

Til slutt konkluderes det med at det patenterte stoffet har en molar absorberende ved frekvens 589 nm produsert av en natriumlampe med:

= (2000 ± 60) (m*cm)^-1

Referanser

1. Atkins, p. 1999. Fysisk kjemi. Omega -utgaver. 460-462.
2. Guiden. Overføring og absorbans. Gjenopprettet fra: Kjemi.Laguia2000.com
3. Miljøtoksikologi. Transmittans, Absorbance and Law of Lambert. Gjenopprettet fra: depot.Innovationumh.er
4. Adventure Physics. Absorbans og transmittans. Gjenopprettet fra: rpfisica.Blogspot.com
5. Sistophotometry. Gjenopprettet fra: Chem.Librettexts.org
6. Miljøtoksikologi. Transmittans, Absorbance and Law of Lambert. Gjenopprettet fra: depot.Innovationumh.er
7. Wikipedia. Absorbans. Gjenopprettet fra: Wikipedia.com
8. Wikipedia. Spektrofotometri. Gjenopprettet fra: Wikipedia.com