Akselerasjon av tyngdekraften hva det er, hvordan den måles og øvelser

De Tyngdekraftsakselerasjon o Gravitasjonsakselerasjon er definert som intensiteten til landgravitasjonsfeltet. Det vil si kraften som dette utøver på ethvert objekt, per masseenhet.

Det er betegnet med den allerede kjente bokstaven G og dens omtrentlige verdi i nærheten av jordoverflaten er 9.8 m/s². Denne verdien kan oppleve små variasjoner med geografisk breddegrad og også med høyden med hensyn til havnivå.

Astronaut i rommet Paseo på jordens overflate. Kilde: Pixabay

Akselerasjonen av tyngdekraften, i tillegg til å ha den nevnte størrelsesorden, har retning og mening. Det er faktisk rettet vertikalt mot jordens sentrum.

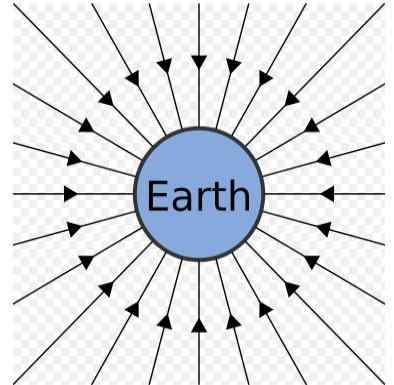Gravitasjonsfeltet på jorden. Kilde: Kilde: Sjlegg [Public Domain]

Gravitasjonsfeltet på jorden kan bli representert som et sett med radielle linjer som peker til sentrum, som det kan sees i forrige figur.

[TOC]

Hva er akselerasjonen av tyngdekraften?

Verdien av akselerasjonen av tyngdekraften i jorden eller på en hvilken som helst annen planet tilsvarer intensiteten til gravitasjonsfeltet den produserer, som ikke er avhengig av objektene som er rundt det, men bare på sin egen masse og dens radius.

Ofte er akselerasjonen av tyngdekraften ofte definert som akselerasjonen som opplever ethvert objekt i fritt fall i nærheten av jordoverflaten.

I praksis er det dette som nesten alltid skjer, som vi vil se i de følgende seksjoner, der Newtons universelle gravitasjonslov vil bli brukt.

Det sies at Newton oppdaget denne berømte loven mens han mediterte på kroppens fall under et tre. Når han følte bløtet til eplet i hodet, visste han umiddelbart at kraften som får eplet til å falle er den samme som får månen til å bane rundt jorden.

Den universelle gravitasjonsloven

En viss eller ikke Apple -legenden, Newton innså at størrelsen på gravitasjonsattraksjonskraften mellom to gjenstander, for eksempel mellom jorden og månen, eller jorden og eplet, måtte være avhengig av massene til disse:

Hvor m₁ Det kan være jordens masse og m_2, Massen til månen eller eple. En større masse, større attraksjon eksisterer blant kroppene. Men på mer avstand, mindre kraft, siden dette må være omvendt proporsjonalt med avstandens kvadrat r som skiller dem:

Kan tjene deg: Elastiske sjokk: I en dimensjon, spesielle tilfeller, øvelser

Dette gjelder uansett hvor store eller små er massene det gjelder. Ved å kombinere disse fakta, ville tyngdekraften forbli på denne måten:

En konstant av proporsjonalitet er nødvendig for å ha denne empiriske loven klar. Newton beregnet konstanten G, slik at formelen beskriver med all presisjon bevegelsene til himmellegemene i omfanget av solsystemet og utover:

Hvor g = 6.67 x 10^-elleve N.m²/kg²

Kjennetegn på gravitasjonskraft

Gravitasjonskraften er alltid attraktiv; det vil si at de to kroppene det påvirker er tiltrukket av hverandre. Det motsatte er ikke mulig, siden de himmelske kroppene er stengt eller åpne (kometer, for eksempel) og en frastøtningskraft aldri kan produsere en lukket bane. Da tiltrekker massene alltid, hva som skjer.

En ganske god tilnærming til jordens virkelige form (m₁) Og månen eller eplet (m₂) er å anta at de har en sfærisk form. Følgende figur er en representasjon av dette fenomenet.

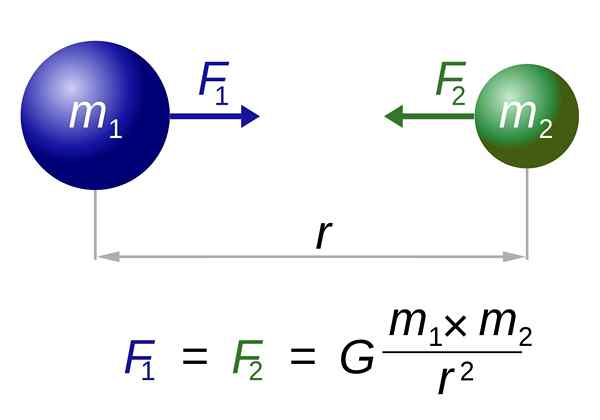Newtons universelle gravitasjonslov. Kilde: I, Dennis Nilsson [CC av 3.0 (https: // creativecommons.Org/lisenser/av/3.0)]

Her er begge kraften utøvd m₁ Om m₂, Som den som utøver m₂ Om m₁, både av like stor størrelsesorden og rettet langs linjen som blir med i sentrene. De blir ikke kansellert, siden de blir brukt på forskjellige objekter.

I alle følgende seksjoner antas det at objekter er homogene og sfæriske, derfor sammenfaller tyngdekraften med dets geometriske sentrum. All konsentrert masse kan antas bare der.

Hvordan måles tyngdekraften på forskjellige planeter?

Tyngdekraften kan måles med en liemeter, et apparat som tjener til å gjøre alvor målt i geofysiske gravimetriske undersøkelser. De er for tiden mye mer sofistikerte enn originalene, men i begynnelsen var de basert på pendelen.

Pendelen består av et tynt, lett og uutholdbart tau av lengde l. En av endene er festet til den ene støtten og den andre henger en masse m.

Når systemet er i likevekt, henger deigen vertikalt, men når den er atskilt fra den, begynner den å svinge en svingbevegelse. Tyngdekraften er ansvarlig for det. For alt som følger, er det gyldig å anta at tyngdekraften er den eneste kraften som virker på pendelen.

Kan tjene deg: Aerostatisk ballong: Historie, egenskaper, deler, hvordan det fungerer

Perioden med sving av pendelen for små svingninger, er gitt av følgende ligning:

Kraften T er ikke avhengig av massen, men av lengden på L og verdien av g. Square Begge medlemmene av ligningen er:

Forholdet mellom T² og L Det er lineært: en linje med skjemaet y = a.x, hvor verdien av til, Skråningen på linjen er nettopp (4π²/g).

Eksperimentere for å bestemme verdien av g

Materialer

- 1 metall sfæritt.

- Tau av flere forskjellige lengder, minst 5.

- Målebånd.

- Transportør.

- Kronometer.

- En støtte for å sette pendelen.

- Milimetering papir eller dataprogram med regneark.

Fremgangsmåte

1. Velg en av strengene og sett sammen pendelen. Mål lengden på tauet + sfærens radius. Dette vil være lengden l.
2. Fjern pendelen fra likevektsposisjonen omtrent 5 grader (id den med transportøren) og la den svinges.
3. Start samtidig stoppeklokken og måle tiden på 10 svingninger. Skriv ned resultatet.
4. Gjenta den forrige prosedyren for de andre lengdene.
5. Finn tiden som tar pendelen for å utføre en svingning (dele hvert av de tidligere resultatene med 10).
6. Firkant hver oppnådd verdier, og oppnår t²
7. I millimeterpapiret, tegne hver verdi av t² På den vertikale aksen, mot den respektive verdien av L på den horisontale aksen. Være i samsvar med enhetene og ikke glem å ta hensyn til feilen for forståelse av instrumentene som brukes: metrisk tape og stoppeklokke.
8. Tegn den beste linjen som passer til grafiske punkter.
9. Finn skråningen m av denne linjen ved å bruke to punkter som tilhører den (ikke nødvendigvis eksperimentelle punkter). Legg til den eksperimentelle feilen.
10. Ovennevnte trinn kan utføres med et regneark og muligheten til å bygge og justere en rett linje.
11. Fra verdien av skråningen til Fjern verdien av g Med sin respektive eksperimentelle usikkerhet.

Standardverdi av g På jorden, på månen og på Mars

Standardverdien av tyngdekraften på jorden er: 9.81 m/s², på 45 av nordlig breddegrad og ved havnivå. Ettersom jorden ikke er en perfekt sfære, verdiene til g De varierer litt, og er større i polene og mindreårige i Ecuador.

De som ønsker å vite verdien i deres lokalitet, kan finne den oppdatert på nettstedet til Metrology Institute of Germany PTB (Physikalisch-Technische Bundesanstalt), i seksjonen Gravity Information System (KRITT).

Det kan tjene deg: Director Vector: Rett ligning, løste øvelser

Tyngdekraften på månen

Gravitasjonsfeltet til månen er blitt bestemt ved analyse av radiosignalene til romprober som går i bane rundt satellitten. Verdien på månens overflate er 1.62 m/s²

Alvorlighetsgraden i Mars

Verdien av g_P For en planet avhenger det av dens masse m og dens radius som følger:

Derfor:

For planeten Mars er følgende data tilgjengelig:

M = 6.4185 x 10²³ kg

R = 3390 km

G = 6.67 x 10^-elleve N.m²/kg²

Med disse dataene vet vi at alvorlighetsgraden av Mars er 3.71 m/s². Naturligvis kan den samme ligningen brukes på månedata eller en hvilken som helst annen planet og estimerer verdien av dens alvorlighetsgrad.

Løst trening: Eplet som faller

Anta at både jorden og et eple har en sfærisk form. Jordens masse er m = 5,98 x 10²⁴ kg og radius er r = 6,37 x 10⁶  m. Massen til eplet er m = 0.10 kg. Anta at det ikke er noen annen styrke bortsett fra tyngdekraften. Fra Newtons universelle gravitasjonslov:

a) Gravitasjonskraften som utøves på eplet.

b) Akselerasjonen opplever av eplet når du slipper det fra en viss høyde, i henhold til Newtons andre lov.

Løsning

a) Eplet (antatt sfærisk, akkurat som jorden) har en veldig liten radius sammenlignet med den landlige radius og er nedsenket i gravitasjonsfeltet. Følgende figur er ikke tydelig, men det er et opplegg i gravitasjonsfeltet g, og Strengh F trent av jorden på eplet:

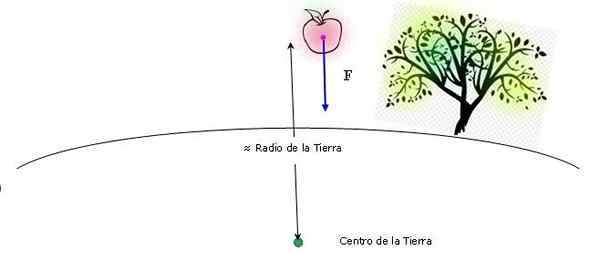Opplegg som viser eples fall i nærheten av jorden. Både størrelsen på eplet og høstens høyde er foraktelig. Kilde: Selvlaget.

Når du bruker Newtons universelle gravitasjonslov, kan avstanden mellom sentrene betraktes som omtrent samme verdi som jordens radius (høyden som eplet faller fra er også ubetydelig sammenlignet med den terrestriske radius). Derfor:

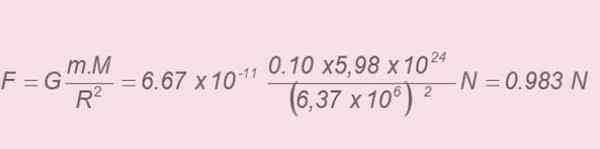
b) I henhold til Newtons andre lov er størrelsen på styrken utøvd på eplet:

F = ma = mg

Hvis verdi er 0.983 n, i henhold til forrige beregning. Utjevning av begge verdiene og deretter å fjerne størrelsen på akselerasjonen oppnås:

mg = 0.983 n

G = 0.983 N/0.10 kg = 9.83 m/s²

Dette er en veldig god tilnærming til standardverdien av tyngdekraften.

Referanser

1. Giancoli, d. (2006). Fysikk: Prinsipper med applikasjoner. Sjette utgave. Prentice Hall. 118-122.
2. Hewitt, Paul. (2012). Konseptuell fysisk vitenskap. Femte utgave. Pearson. 91 - 94.
3. Rex, a. (2011). Fundamentals of Physics. Pearson. 213-221.