Bølgeamplitudeegenskaper, formler og trening

De Bølgeamplitude Det er den maksimale forskyvningen som et punkt opplever i en bølge med hensyn til likevektsposisjonen. Bølgene manifesterer seg overalt og mange måter i verden rundt oss: i havet, i lyden og i tauet til et instrument som produserer det, i lyset, på jordens overflate og mye mer.

En måte å produsere bølger og studere dens oppførsel er å observere vibrasjonen av et tau som har en fast slutt. Ved å produsere en forstyrrelse i den andre enden, svinger hver partikkel av tauet og med det overføres energien i forstyrrelsen i form av en rekke pulser gjennom hele tiden.

Bølger manifesterer seg på mange måter i naturen. Kilde: Pixabay.

Når energien sprer seg, vedtar tauet som antas å være perfekt elastisk, den typiske sinusformede formen med rygger og daler vist på figuren som vises nedenfor i følgende avsnitt.

[TOC]

Kjennetegn og betydning av bølgeamplitude

Amplitude A er avstanden mellom toppen og referanseaksen eller nivå 0. Hvis du er foretrukket, mellom en dal og referanseaksen. Hvis forstyrrelsen i tauet er mild, er amplituden A liten. Hvis tvert imot forstyrrelsen er intens, vil amplituden være større.

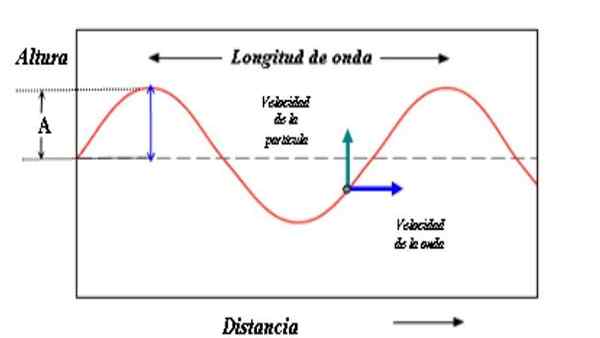En modell for å beskrive bølgen består av en sinusformet kurve. Bølgeamplitude er avstanden mellom en kam eller dal og referanseaksen. Kilde: Paco [CC BY-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

Verdien av amplituden er også et mål på energien som bærer bølgen. Det er intuitivt at stor amplitude er assosiert med større energier.

Faktisk er energien proporsjonal med kvadratet av amplituden, som uttrykte matematisk er:

Jeg ∝a²

Kan tjene deg: gjensidig induktans: formel/koeffisient, applikasjoner, øvelser

Der jeg er intensiteten til bølgen, i sin tur relatert til energi.

Den typen bølge produsert i eksemplet tauet, tilhører kategorien mekaniske bølger. En viktig egenskap er at hver partikkel på tauet alltid forblir veldig nær sin likevektsposisjon.

Partiklene beveger seg ikke eller beveger seg gjennom tauet. De varierer opp og ned. Dette er indikert i toppskjemaet med den grønne pilen, men bølgen sammen med sin energi, reiser fra venstre til høyre (blå pil).

Bølger som sprer seg i vannet gir de nødvendige bevisene for å overbevise seg om dette. Å observere bevegelsen av et ark som har falt i et tjern, kan se at hun ganske enkelt svinger sammen med vannets bevegelse. Det går ikke veldig langt, i det minste klart, at det er andre krefter som gir andre bevegelser.

Bølgemodellen vist på figuren består av et repeterende mønster der avstanden mellom to rygger er bølgelengde λ. Hvis du vil, skiller bølgelengden også to identiske punkter fra bølgen, selv når de ikke er på toppen.

Den matematiske beskrivelsen av en bølge

Naturligvis kan bølgen beskrives ved en matematisk funksjon. Periodiske funksjoner som bihule og kosinus er det ideelle for oppgaven, enten du vil representere bølgen både i verdensrommet og i tid.

Hvis vi kaller den vertikale aksen i figuren og den horisontale aksen vi kaller den "t", uttrykkes bølgen over tid over tid av:

y = a cos (ωt + Δ)

For denne ideelle bevegelsen svinger hver taupartikkel med enkel harmonisk bevegelse, som har sin opprinnelse takket være en kraft som er direkte proporsjonal med forskyvningen som er gjort av partikkelen.

Kan tjene deg: Dirac Jordan Atomic Model: Egenskaper og postulater

I den foreslåtte ligningen er a, ω og δ parametere som beskriver bevegelsen, og er til amplitude Tidligere definert som den maksimale forskyvningen som partikkelen opplever med hensyn til referanseaksen.

Kosinas argument kalles Bevegelsesfase Og Δ er Fasekonstant, Hva er fasen når t = 0. Både kosinusfunksjonen og sinusfunksjonen er passende for å beskrive en bølge, siden de bare skiller seg fra hverandre π/2.

Det er vanligvis mulig å velge t = 0 med Δ = 0 for å forenkle uttrykket, oppnå:

y = a cos (ωt)

Når bevegelsen er repeterende i både rom og tid, er det en karakteristisk tid som er periode t, definert som tiden det tar for partikkelen å utføre en fullstendig svingning.

Bølgebeskrivelse i tid: Karakteristiske parametere

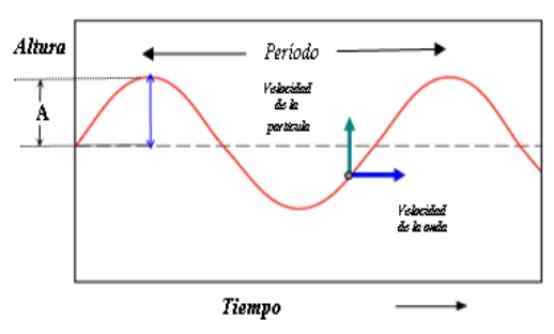Denne figuren viser bølgebeskrivelsen i tide. Avstanden mellom rygger (eller daler) tilsvarer nå bølgeperioden. Kilde: Paco [CC BY-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]]

Nå gjentar både brystet og kosinuset verdien når fasen øker i verdien 2π, slik at:

ωt = 2π → ω = 2π /t

Ω kalles Vinkelfrekvens av bevegelse Og det har dimensjoner av det inverse av tiden, og er dets enheter i det internasjonale systemet Radián / Second eller Second^-1.

Endelig kan du definere Bevegelsesfrekvens F, som den omvendte eller gjensidige i perioden. Representerer i antall rygger per tidsenhet, i hvilket tilfelle:

F = 1/t

Ω = 2πf

Både F og ω har samme dimensjoner og enheter. I tillegg til det andre^-1, som kalles Hertz eller Hertzio, det er vanlig å høre om Revolusjoner per sekund enten omdreininger per minutt.

Bølgehastighet v, som må understrekes at det ikke er det samme som den som er opplevd av partiklene, kan det lett beregnes hvis bølgelengden λ og frekvens f er kjent:

Det kan tjene deg: lysende kropper: egenskaper og hvordan de genererer sitt eget lys

V = λf

Hvis svingningen som partiklene opplever er av den enkle harmoniske typen, avhenger vinkelfrekvensen og frekvensen bare av arten av oscillerende partikler og egenskapene til systemet. Bølgenes amplitude påvirker ikke disse parametrene.

For eksempel, når du spiller en musikalsk lapp på en gitar, vil lappen alltid ha samme tone, selv om den blir berørt med større eller mindre intensitet, på denne måten vil en do alltid høres ut som en do, selv om den blir hørt sterkere eller mykere i en komposisjon, enten på et piano eller på gitar.

I naturen blir bølger som transporteres i et materielt miljø i alle retninger dempet fordi energien forsvinner. Av denne grunn avtar amplituden med inverse av avstanden r til kilden, å være mulig å bekrefte det:

A∝1/r

Trening løst

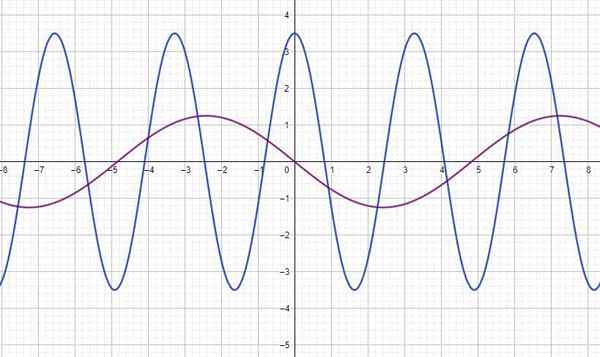
Figuren viser funksjonen y (t) for to bølger, hvor og er i meter og t på få sekunder. For hvert funn:

A) Amplitude

b) periode

c) frekvens

d) Ligningen til hver bølge når det gjelder bryster eller cosenos.

Svar

a) Den måles direkte fra grafen, ved hjelp av rutenettet: Blue Wave: A = 3.5m; Fuchsia Wave: A = 1.25 m

b) Den leser også grafen, og bestemmer separasjonen mellom to topper eller daler, påfølgende: blå bølge: t = 3.3 sekunder; Fuchsia bølge t = 9.7 sekunder

c) Det beregnes med å huske at frekvensen er gjensidig av perioden: Blue Wave: F = 0.302 Hz; Fuchsia Wave: F = 0.103 Hz.

d) blå bølge: y (t) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Fuchsia bølge: y (t) = 1.25 Synd (0.65t) = 1.25 kos (0.65T+1.57)

Merk at fuchsia -bølgen er utdatert π/2 med hensyn til blått, og er mulig å representere den med en sinusfunksjon. Eller fortrengt kosinus π/2.