Kanter på en kube

Hva er kanten av en kube?

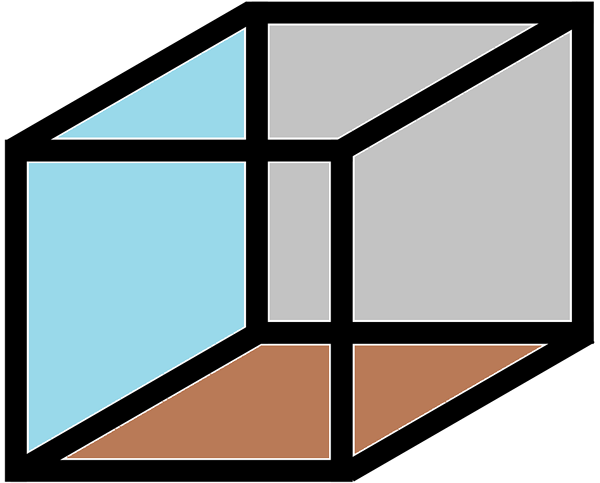
De kanten av en kube Det er en kant av det: det er linjen som forbinder to hjørner eller hjørner. En kant er linjen der to sider av en geometrisk figur blir oppfanget. En kube har 12 kanter.

Den forrige definisjonen er generell og gjelder enhver geometrisk figur, ikke bare for kuben. Når det gjelder en flat figur, tilsvarer kantene sidene av nevnte figur.

Det kalles parallellpiped til en geometrisk figur med seks ansikter i form av parallellogrammer, hvorav motsetningene er like og parallelle med hverandre.

I det spesielle tilfellet der ansiktene er firkant.

Måter å identifisere kantene på en kube

For en bedre illustrasjon kan hverdagsobjekter brukes til å bestemme hvilke som er kantene på en kube nøyaktig.

1- Armando en papirbit

Hvis du kan se hvordan en papir- eller pappbøtte er bygget, kan du se hva kantene dine er. Det begynner å tegne et kors som figuren og visse linjer inni er merket.

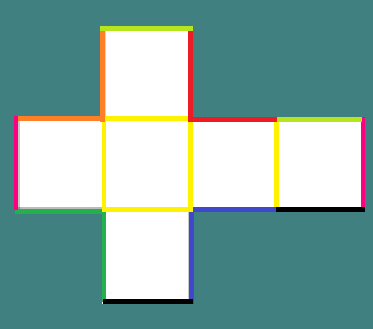
Hver av de gule linjene representerer en fold, som vil være en kant av kuben (kant).

Tilsvarende vil hvert par linjer som har samme farge danne en kant når de blir med. Totalt har en kube 12 kanter.

2- Tegning av en kube

En annen måte å se hva som er kantene på en kube er å observere hvordan den trekkes. Du starter med å tegne et kvadrat med side L; Hver side av torget er en kant av kuben.

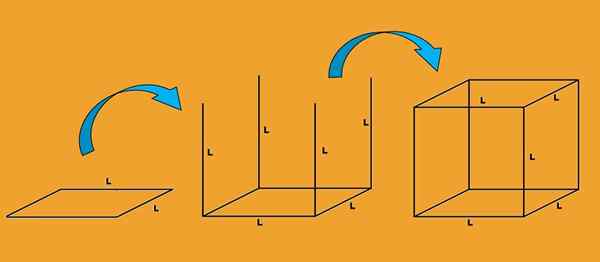
Deretter trekkes fire vertikale linjer fra hvert toppunkt, og lengden på hver av disse linjene er l. Hver linje er også en bøtte kant.

Til slutt tegnes en annen firkant L, slik at dets toppunkt sammenfaller med enden av kantene trukket i forrige trinn. Hver av sidene av dette nye torget er en kant av kuben.

3- Rubik Cube

For å illustrere den geometriske definisjonen som skjedde i begynnelsen, kan du se en Rubik Cube.

Hvert ansikt har en annen farge. Kantene er representert av linjen der ansiktene blir oppfanget med forskjellige farger.

Euler Teorem

Eulers teorem for Polyhedros sier at gitt en polyhedron, antall ansikter C pluss antall hjørner V er lik antall kanter til pluss 2. Det vil si C+V = A+2.

I de forrige bildene kan det sees at en kube har 6 ansikter, 8 hjørner og 12 kanter. Derfor oppfyller det Euler Teorem for Polyhedra, siden 6+8 = 12+2.

Å kjenne lengden på en kant av en kube er veldig nyttig. Hvis lengden på en kant er kjent, er lengden på alle kantene kjent, som kan få visse kubedata, for eksempel volumet.

Volumet til en kube er definert som l³, hvor L er lengden på kantene. For å kjenne kubenes volum er det bare nødvendig å vite verdien av l.