Ortonormale baseegenskaper, eksempler og øvelser

EN Ortonormal base Det er dannet med vinkelrett vektorer med hverandre og hvis modul også er verdt 1 (enhetsvektorer). Husk at en base B i et vektorrom V, Det er definert som et sett med lineært uavhengige vektorer som er i stand til å generere dette rommet.

På sin side er et vektorrom en abstrakt matematisk enhet mellom hvis elementer er vektorer, generelt assosiert med fysiske størrelser som hastighet, styrke og forskyvning eller også til matriser, polynomer og funksjoner.

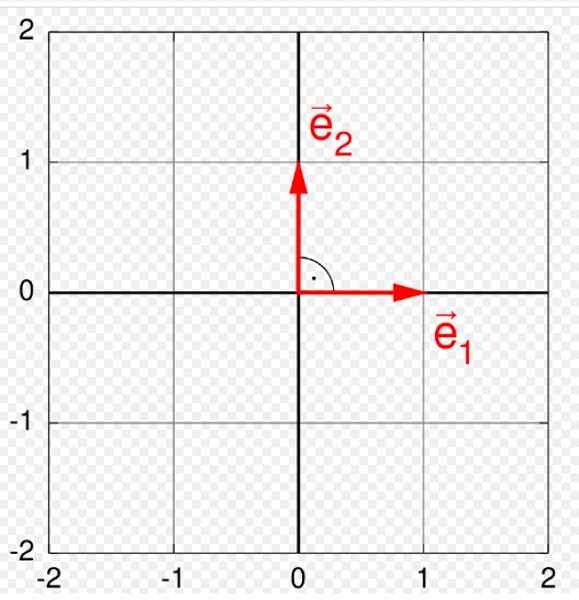
Figur 1. Ortonormal base i flyet. Kilde: Wikimedia Commons. Quartl [CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)].

Vektorer har tre særegne elementer: størrelse eller modul, retning og mening. En ortonormal base er spesielt nyttig å representere og operere med dem, fordi enhver vektor som tilhører et visst vektorrom V, Det kan skrives som en lineær kombinasjon av vektorene som danner den ortonormale basen.

På denne måten blir operasjoner mellom vektorer, for eksempel sum, subtraksjon og de forskjellige typer produkter definert i nevnte rom analysert analytisk.

Blant de mest brukte fysikkens baser er basen dannet av enhetsvektorer Yo, J og k som representerer de tre særegne retningene fra tre -dimensjonalt rom: høy, bred og dybde. Disse vektorene er også kjent under navnet til Enhetlige kanoniske vektorer.

Hvis det i stedet blir jobbet vektorer på et fly, ville det være nok med to av disse tre komponentene, mens bare en.

[TOC]

Baserer egenskaper

1- En base B Det er det minste mulige sett med vektorer som genererer vektorrommet V.

2- Elementene i B De er lineært uavhengige.

3- Enhver base B av et vektorrom V, tillater å uttrykke alle vektorene til V som en lineær kombinasjon av den, og denne formen er unik for hver vektor. Derfor a B Det er også kjent som Generatorsystem.

4- Det samme vektorrommet V kan ha forskjellige baser.

Kan tjene deg: sentrifugal kraft: Formler, hvordan den beregnes, eksempler, øvelser

Eksempler på baser

Under flere eksempler på ortonormale baser og baser generelt:

Den kanoniske basen i ℜ ⁿ

Også kalt naturlig base eller standard base av ℜ ⁿ, Hvor ℜ ⁿ Det er plass n-dimensjonal, For eksempel er tre -dimensjonalt rom ℜ ³. Til verdien av n Det kalles dimensjon av vektorrommet og betegner som Dim (v).

Alle vektorer som tilhører ℜ ⁿ De er representert av N-USA Bestilt. For plass ℜⁿ, Den kanoniske basen er:

og₁ =; og₂ =; og_n =

I dette eksemplet har vi brukt notasjonen med parentes eller "parentes" og fet skrift for enhetsvektorer og₁, og₂, og₃..

Den kanoniske basen i ℜ³

Familievektorer Yo, J og k De innrømmer den samme representasjonen, og de er nok til at tre representerer vektorene i ℜ ³:

Yo =; J =;  k =

Det betyr at basen kan uttrykkes som følger:

B = ; ;

For å bekrefte at de er lineært uavhengige, er determinanten dannet med dem vektorer ikke -null og også lik 1:

Det må også være mulig å skrive hvilken som helst vektor som tilhører ℜ ³ Som en lineær kombinasjon av dem. For eksempel en kraft hvis rektangulære komponenter er f_x = 4 n, f_og = -7 n og f_z= 0 n ville bli skrevet i en vektorform som følger:

F = N = 4Yo -7J + 0k N.

Derfor Yo, J og k gjøre opp et ℜ generatorsystem ³.

Andre Ortonormale baser i ℜ³

Standardbasen beskrevet i forrige seksjon er ikke den eneste Ortonormale basen i ℜ³. Her har vi for eksempel basene:

B₁ = ; ;

B₂ = ; ;

Det kan påvises at disse basene er ortonormale, for dette husker vi forholdene som må oppfylles:

Kan tjene deg: bølgende optikk

-Vektorer som danner basen må være ortogonale for hverandre.

-Hver av dem må være enhetlige.

Vi kan bekrefte at det vet at determinanten som er dannet av dem, må være ikke -null og lik 1.

Base b₁ Det er nettopp det av sylindriske koordinater ρ, φ og z, en annen måte å uttrykke vektorer i rommet.

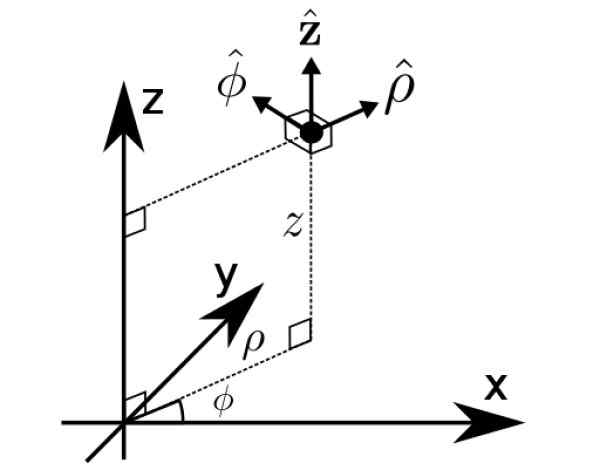Figur 2. Sylindriske koordinater. Kilde: Wikimedia Commons. Math Buff [CC BY-S (https: // CreativeCommons.Org/lisenser/by-SA/4.0)].

Løste øvelser

- Oppgave 1

Vis at basen B = ; ; er Ortonormal.

Løsning

For å vise at vektorene er vinkelrett på hverandre, vil vi bruke skalarproduktet, også kalt internt eller produktpunkt for to vektorer.

La alle to vektorer eller og v, Scalar -produktet ditt er definert av:

eller • v = eller.v. cosθ

For å skille vektorene fra modulene deres vil vi bruke fet skrift for de første og normale bokstavene for sistnevnte. θ er vinkelen mellom eller og v, Derfor hvis de er vinkelrett, betyr det at θ = 90º og skalarproduktet er ugyldig.

Alternativt, hvis vektorene er gitt i form av komponentene deres: eller = x, eller_og,eller_z > og v = x, v_og,v_z > Skalarproduktet av begge, som er kommutativt, beregnes på denne måten:

eller • v = eller_x .v_x + eller_og .v_og + eller_z .v_z

På denne måten er skalarproduktene mellom hvert par vektorer henholdsvis:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

For den andre tilstanden beregnes modulen til hver vektor, som er oppnådd av:

│u │ = √ (u_x² + eller_og² + eller_z²)

Dermed er modulene til hver vektor:

│ = √ [(3/5)² + (4/5)²  + 0²)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0²)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

Det kan tjene deg: Andre likevektstilstand: Forklaring, eksempler, øvelser

│ = √ [0² + 0²  + 1²)] = 1

Derfor er de tre enhetsvektorene. Til slutt er determinanten de danner ikke null og lik 1:

- Oppgave 2

Skriv vektorkoordinatene W = I form av forrige base.

Løsning

For å gjøre det brukes følgende teorem:

La B = v₁, v₂, v₃,.. v_n En ortonormal base i rom V med innenriksprodukt, vektoren W Det er representert av B som følger:

W = <W•v₁> v₁ + <W•v₂> v₂ +<W•v₃> v₃ +.. <W•v_n> v_n

Dette betyr at vi kan skrive vektoren ved base B, gjennom koeffisienter <W•v₁>, <W•v₂>, ..  <W•v_n>, som du må beregne de angitte skalarene:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

Med oppnådd skalarprodukter er det bygget en matrise, kalt Koordinatmatrise av w.

Derfor koordinater W I base B er de uttrykt gjennom:

[W]_B= [(18/5); (1/5); 1]

Koordinatmatrisen er ikke vektoren, siden en vektor ikke er den samme som koordinatene. Dette er bare et sett med tall som tjener til å uttrykke vektoren ved en gitt base, ikke vektoren som sådan. De er også avhengige av den valgte basen.

Til slutt, etter teoremet, vektoren W ville bli uttrykt som følger:

W = (18/5) v₁ + (1/5) v₂ + v₃

Med: v₁ =; v₂ =; v₃ =, Det vil si basevektorene B.

Referanser

1. Larson, r. Grunnleggende om lineær algebra. 6. Utgave. Cengage Learning.
2. Larson, r. 2006. Beregning. 7. Utgave. Volum 2. McGraw Hill.
3. Salas, J. lineær algebra. Emne 10. Ortonormale baser. Gjenopprettet fra: OCW.UC3M.er.
4. Sevilla University. Sylindriske koordinater. Vektorbase. Gjenopprettet fra: Laplace.oss.er.
5. Wikipedia. Ortonormal base. Gjenopprettet fra: er.Wikipedia.org.