Konjugert binomial hvordan det løses, eksempler, øvelser

EN Konjugert binomial Fra en annen binomial er en der de bare er forskjellige med et tegn på operasjonen. Binomialen, som navnet tilsier, er en algebraisk struktur som består av to begreper.

Noen eksempler på binomialer er: (A + B), (3M - N) og (5x - y). Og deres respektive konjugerte binomials er: (a - b), (-3m - n) og (5x + y). Som det kan sees umiddelbart, er forskjellen i tegnet.

Figur 1. En binomial og dens konjugerte binomial. De har de samme vilkårene, men er forskjellige i tegnet. Kilde: f. Zapata.

En binomial multiplisert med dets konjugat resulterer i et bemerkelsesverdig produkt som brukes mye i algebra og vitenskap. Resultatet av multiplikasjon er subtraksjon av rutene til vilkårene i den opprinnelige binomial.

For eksempel, (X - y) Det er en binomial og dens konjugat er (x + y). Deretter er produktet av de to binomialene forskjellen på kvadratene på vilkårene:

(X - y).(x + y) = x² - og²

[TOC]

Hvordan løses en konjugert binomial?

Regelen som er beskrevet med de konjugerte binomialene er som følger: 

Produktet av to konjugatbinomialer er lik kvadratet på det første termmen minus kvadratet på den andre termen. Dette resultatet kalles kvadratforskjell.

Som et eksempel på anvendelse vil vi begynne med å demonstrere det forrige resultatet, som kan gjøres ved hjelp av produktets distribusjonseiendom med hensyn til den algebraiske summen.

(x - y) (x + y) = x.x + x.og - og.X - y.og

Den forrige multiplikasjonen ble oppnådd etter disse trinnene:

- Den første termin av den første binomialen multipliseres med den første termin av den andre

- Så den første av den første, for den andre av det andre

- Så den andre av den første for den første av det andre 

- Endelig den andre av den første for den andre av sekundet.

Kan tjene deg: vektor algebra

La oss nå gjøre en liten endring ved hjelp av kommutativ eiendom: og.x = x.og. Det forblir slik:

(x - y) (x + y) = x.x + x.y - x.og - og.og

Ettersom det er to like vilkår, men ellers (fremhevet i farger og understreket), blir de kansellert og forenklet:

(x - y) (x + y) = x.X - y.og

Til slutt brukes det at det å multiplisere et tall av seg selv, tilsvarer å løfte det firkantet, så x.x = x² og også og.y = y².

På denne måten, det som hadde blitt påpekt i foregående avsnitt, at produktet av en sum for dens forskjell er forskjellen på rutene:

(X - y).(x + y) = x² - og²

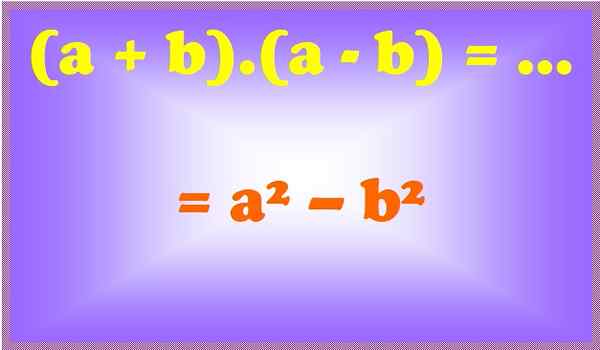Figur 2. En sum for forskjellen er en forskjell på firkanter. Kilde: f. Zapata.

Eksempler

- Konjugerte binomialer av forskjellige uttrykk

Eksempel 1

Finn konjugatet til (og² - 3Y).

Svar: (og² + 3Y)

Eksempel 2

Få produktet av (og² - 3y) for sin konjugat.

Svar: (og² - 3y) (og² + 3y) = (og²)² - (3Y)² = y⁴ - 3² og² = y⁴ - 9y²

Eksempel 3

Utvikle produktet (1 + 2A).(2a -1).

Svar: Det forrige uttrykket tilsvarer (2a + 1).(2a -1), det vil si at det tilsvarer produktet av en binomial for dets konjugat.

Det er kjent at produktet av en binomial for dets konjugerte binomial er lik forskjellen på rutene til binomialuttrykkene:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Eksempel 4

Skriv produktet (x + y + z) (x - y - z) som en forskjell på firkanter.

Svar: Vi kan assimilere trinomialene før formen av konjugerte binomialer, og gjøre nøye bruk av parenteser og firkantede parenteser:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

På denne måten kan forskjellen på firkanter brukes:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y+z)] = x² - (Y+z)²

Eksempel 5

Uttrykke produktet (m² - m -1).(m² + m -1) som en forskjell i firkanter.

Kan tjene deg: 120 delinger

Svar: Det forrige uttrykket er produktet av to trinomialer. For det første må det skrives om som produkt av to konjugerte binomialer:

(m² - m -1) (m² + m -1) = (m² - 1 - m) (m² -1 + m) = [(m² -1) - m].[(m² -1) +m)]

Vi bruker det faktum at produktet av en binomial av dets konjugat er den kvadratiske forskjellen på dens vilkår, som forklart:

[(m² -1) - m].[(m² -1) +m)] = (m² -1)² - m²

Øvelser

Som alltid begynner det med de enkleste øvelsene, og da øker kompleksitetsnivået.

- Oppgave 1

Escriba (9 - a²) som et produkt.

Løsning

For det første omskriver vi uttrykket som en forskjell på firkanter, for å bruke det som forklarte tidligere. Derfor:

(9 - a²) = (3² - til²)

Vi faktor, som tilsvarer å skrive denne forskjellen på firkanter som et produkt, som forespurt i uttalelsen:

(9 - a²) = (3² - til²) = (3 + a) (3 -a)

- Oppgave 2

Faktoriser 16x² - 9y⁴.

Løsning

Faktor et uttrykk betyr å skrive det som et produkt. I dette tilfellet er det nødvendig å tidligere omskrive uttrykket, for å oppnå en forskjell på firkanter.

Det er ikke vanskelig å gjøre det, siden nøye observerende, alle faktorene er perfekte firkanter. For eksempel 16 er kvadratet av 4, 9 er kvadratet av 3, og⁴ er kvadratet av og² og x² er kvadratet av X:

16x² - 9y⁴  = 4²x² - 3²og⁴ = 4²x²  - 3²(og²)²

Så blir det vi allerede vet brukt: at en forskjell i firkanter er produktet av konjugerte binomialer:

(4x)² - (3 og²)² = (4x - 3 og²) . (4x + 3 og²)

- Øvelse 3

Skriv (A - B) som et binomialt produkt

Løsning

Den forrige forskjellen skal skrives som kvadratiske forskjeller

(√a)² -(√B)²

Deretter brukes det at forskjellen i firkanter er produktet av de konjugerte binomialene

Kan tjene deg: Reduksjon av lignende vilkår

(√a - √B) (√a + √B)

- Oppgave 4

En av bruken av den konjugerte binomialen er rasjonaliseringen av algebraiske uttrykk. Denne prosedyren består i å eliminere røttene til nevneren til et brøkuttrykk, som ved flere anledninger letter driften. Det blir bedt om å bruke den konjugerte binomialen for å rasjonalisere følgende uttrykk:

√ (2 -x) / [√3 - √ (2+x)]]

Løsning

Den første er å identifisere den konjugerte binomialen til nevneren: [√3 + √ (2 + x)]].

Nå multipliserer vi teller og nevner av det opprinnelige uttrykket med den konjugerte binomialen:

√ (2 -x) [√3+√ (2+x)] /[√3 - √ (2+x)].[√3 + √ (2 + x)]

I nevneren av det forrige uttrykket gjenkjenner vi produktet av en forskjell med en sum, som vi allerede vet som tilsvarer forskjellen på rutene til binomialene:

√ (2-x) .[√3 + √ (2 + x)] /(√3)² - [√ (2+x)]² 

Forenkle nevneren er:

√ (2-x).[√3+√ (2+x)] / [3 - (2+x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Nå tar vi vare på telleren, som vi vil bruke produktets distribusjonseiendom med hensyn til summen:

√ (2-x) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

I det forrige uttrykket gjenkjenner vi produktet av binomial (2-x) for dets konjugat, som er det bemerkelsesverdige produktet som tilsvarer forskjellen på firkanter. På denne måten oppnås et rasjonalisert og forenklet uttrykk endelig:

[√ (6-3x) + √ (4-x²)] / (1 - x)

- Oppgave 5

Utvikle følgende produkt ved å bruke egenskapene til den konjugerte binomialen:

[2^{(x + 3y)} - 3^{(x - 3y)}].[2^{(x + 3y)} + 3^{(x - 3y)}]

Løsning

4. plass^{(2x + 6y)} - 9^{(2x - 6y)} = 4a^(2x) .til^(6y) - 9^(2x) .til^(-6y)= [4a^(6y) - 9^(-6y)] .til^(2x)

Den imøtekommende leseren vil ha lagt merke til den vanlige faktoren som har blitt fremhevet i farger.

Referanser

1. Baldor, a. 1991. Algebra. Venezuelansk kulturell redaksjon S.TIL.
2. González J. Konjugerte binomiale øvelser. Gjenopprettet fra: Akademi.Edu.
3. Matematikk Alex. Bemerkelsesverdige produkter. Gjenopprettet fra YouTube.com.
4. Math2me. Konjugerte binomials/ bemerkelsesverdige produkter. Gjenopprettet fra YouTube.com.
5. Konjugerte binomiale produkter. Gjenopprettet fra: LMS.COLBACHENLINEA.MX.
6. Vitual. Konjugerte binomialer. Gjenopprettet fra: YouTube.com.