Sensitivt varmetekonsept, formler og øvelser løst

Han Følsom varme Det er den termiske energien som leveres til et objekt som fører til at temperaturen øker. Det er det motsatte av latent varme, der termisk energi ikke øker temperaturen, men fremmer en faseendring, for eksempel fra fast til væske.

Et eksempel tydeliggjør konseptet. Anta at vi har en gryte med vanntemperatur på 20 ° C. Når vi plasserer det i hornet, øker varmen på vannets temperatur sakte til 100 ° C (koketemperatur på vannet ved havnivået). Varmen som leveres kalles sensitiv varme.

Varmen som varmer opp hendene er følsom varme. Kilde: Pixabay

Når vannet når koketemperaturen, øker ikke varmen som leveres av Hornilla lenger vanntemperaturen, som forblir ved 100 ° C.  I dette tilfellet investeres den termiske energien som leveres i fordampende vann. Varmen som leveres er latent fordi den ikke økte temperaturen, men forårsaket en endring av væskefasen til gassfasen.

Det er et eksperimentelt faktum at den følsomme varmen som er nødvendig for å oppnå en viss temperaturvariasjon er direkte proporsjonal med den variasjonen og objektets masser.

[TOC]

Konsept og formler

Det har blitt observert at bortsett fra masse- og temperaturforskjell, avhenger sensitiv varme også av materialet. Av denne grunn kalles proporsjonalitetskonstanten mellom den følsomme varmen og produktets produkt ved temperaturforskjellen den spesifikke varmen.

Mengden sensitiv varme som leveres avhenger også av hvordan prosessen blir utført. For eksempel er det annerledes hvis prosessen utføres med konstant volum enn konstant trykk.

Formelen for sensitiv varme i en prosess isobarisk, Det vil si konstant press, det er som følger:

Q = CP . m (tF - TYo)

I forrige ligning Q Det er den følsomme varmen som leveres til massen objekt m, som har hevet sin opprinnelige temperatur T_Yo Inntil den endelige verdien Tf. I forrige ligning vises det også cp, som er den spesifikke varmen til materialet ved konstant trykk fordi prosessen er blitt utført på denne måten.

Merk at sensitiv varme er positiv når den blir absorbert av objektet og forårsaker en temperaturøkning.

I tilfelle at en gass inngått i en stiv beholder blir levert, vil prosessen være isokorisk, det vil si ved konstant volum; Og den sensitive varmeformelen vil bli skrevet slik:

Kan tjene deg: bølgende bevegelse: egenskaper, bølger typer, eksempler

Q = cv. m . (TF - TYo)

Adiabatiske koeffisienten γ

Forholdet mellom den spesifikke varmen ved konstant trykk og den spesifikke varmen ved konstant volum for det samme materialet eller stoffet kalles Adiabatisk koeffisient, som vanligvis betegnes med Gamma Gamma y -bokstaven.

Han Adiabatisk koeffisient er større enn enheten. Varmen som er nødvendig for å heve temperaturen til en kropp av et gram masse til en karakter er større i en isobarisk prosess enn i en isokorisk.

Dette er fordi i det første tilfellet er en del av varmen brukt til å utføre mekanisk arbeid.

I tillegg til den spesifikke varmen, er varmekapasiteten til et legeme vanligvis definert. Dette er mengden varme som er nødvendig for å heve temperaturen på kroppen en centigrade -grad.

Varmekapasitet c

Varmekapasitet er betegnet med C store bokstaver, mens den spesifikke varmen med c Nedgang. Forholdet mellom begge beløpene er:

C = c⋅ m

Hvor m Det er massen i kroppen.

Molar spesifikk varme brukes også, som er definert som mengden sensitiv varme som er nødvendig for å heve seg til en celsius eller kelvin -temperatur.

Spesifikk varme i faste stoffer, væsker og gasser

Den spesifikke molarvarmen til de fleste faste stoffer har en verdi nær 3 ganger R, hvor R Det er den universelle konstanten av gasser. R = 8.314472 J/(mol ℃).

For eksempel har aluminium spesifikk molarvarme 24.2 J/(mol ℃), Kobber 24,5 J/(mol ℃), gull 25,4 J/(mol ℃), og søtt jern 25.1 J/(mol ℃). Merk at disse verdiene er i nærheten av 3R = 24,9 J/(mol ℃).

På den annen side, for de fleste gasser er den spesifikke varmen nær N (r/2), hvor er n et heltall og R Det er den universelle konstanten av gasser. Heltallet n er relatert til antall grader av molekylets frihet som danner gassen.

For eksempel, i en ideell monoatomisk gass, hvis molekyl bare har de tre frihetsgrader, er den spesifikke molare varmen til konstant volum 3 (R/2). Men hvis det er en ideell diatomisk gass, er to rotasjonsgrader i tillegg, så cv = 5 (r/2).

Kan tjene deg: halvsirkel: Hvordan beregne omkretsen, området, centroid, øvelser

I de ideelle gassene er følgende forhold mellom den spesifikke varmevarmen og konstant volum oppfylt: cp = cv + R.

Side omtale fortjener vann. I flytende tilstand ved 25 ℃ vann har cp = 4.1813 J/(G ℃), Vanndamp ved 100 grader Celsius har cp = 2.080 J/(G ℃) Og vannis til null grad Celsius har cp = 2.050 J/(G ℃).

Forskjell med latent varme

Materie kan finnes i tre stater: fast, flytende og gassformig. For å endre tilstanden er det nødvendig med energi, men hvert stoff reagerer på den på en annen måte i henhold til dens molekylære og atomegenskaper.

Når et fast stoff smelter eller en væske fordamper, forblir objektets temperatur konstant til alle partikler har endret status.

Derfor er det mulig at ett stoff samtidig er i likevekt i to faser: fast - væske eller væske - damp, for eksempel. En mengde stoff kan passere fra en tilstand til en annen ved å tilsette eller fjerne litt varme, mens temperaturen forblir fast.

Varmen som leveres til et materiale får partiklene til å vibrere raskere og øke den kinetiske energien. Dette oversettes til en temperaturøkning.

Det er mulig at energien de skaffer seg er så stor at de ikke lenger vender tilbake til likevektsposisjonen og øker separasjonen mellom dem. Når dette skjer øker ikke temperaturen, men stoffet passerer fra fast til væske eller gassvæske.

I varmen som er nødvendig for at dette skal skje, er det kjent som latent varme. Derfor er latent varme varme som et stoff kan endre fase.

Her er forskjellen med sensitiv varme. Et stoff som absorberer sensitiv varme øker temperaturen og forblir i samme tilstand.

Hvordan beregne latent varme?

Den latente varmen beregnes med ligning:

Q = m . L

Hvor L Det kan være den spesifikke varmen ved fordampning eller fusjon. Enhetene til L De er energi/masse.

Forskere har gitt en rekke varmen i. Således er det for eksempel reaksjonsvarmen, forbrenningsvarmen, størkningsvarmen, oppløsningsvarmen, sublimeringsvarmen og mange andre.

Kan tjene deg: Kinetisk energi: Kjennetegn, typer, eksempler, øvelser

Verdiene til mange av disse varmetypene for forskjellige stoffer er tabulert.

Løste øvelser

Eksempel 1

Anta en som har en 3 kg masse aluminium. Opprinnelig er det ved 20 ° C, og du vil heve temperaturen opp til 100 ° C. Beregn den nødvendige sensitive varmen.

Løsning

Først må vi kjenne den spesifikke varmen til aluminium

cp = 0,897 j / (g ° C)

Så mengden varme som trengs for å varme opp aluminiums stykke vil være

Q = cp M (TF - Ti) = 0,897 * 3000 * (100 - 20) J

Q = 215280 J

Eksempel 2

Beregn mengden varme som trengs for å varme opp 1 liter vann fra 25 ° C til 100 ° C ved havnivå. Uttrykke resultatet også i kilokalorier.

Løsning

Det første vi bør huske er at 1 liter vann veier 1 kg, det er 1000 gram.

Q = cp m (tf - ti) = 41813 j/(g ℃) * 1000 g * (100 ℃ - 25 ℃) = 313597,5 j

Caloria er en energienhet som er definert som den følsomme varmen som er nødvendig for å heve et gram vann til en Celsius. Derfor tilsvarer 1 kalori.

Q = 313597,5 J * (1 Cal / 4,1813 J) = 75000 kalk = 75 kcal.

Eksempel 3

Et stykke 360,16 grammateriale varmes opp fra 37 ℃ til 140 ℃. Den termiske energien som leveres er 1150 kalorier.

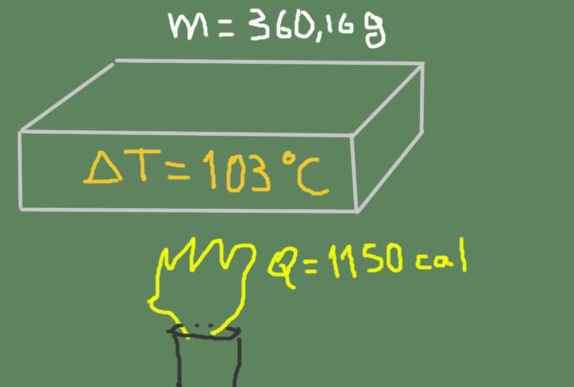Oppvarming av prøven. Kilde: Selvlaget.

Finn den spesifikke varmen på materialet.

Løsning

Vi kan skrive den spesifikke varmen basert på sensitiv varme, masse- og temperaturvariasjon i henhold til formelen:

cp = Q /(m Δt)  

Erstatte dataene vi har følgende:

cp = 1150 cal / (360,16 g * (140 ℃ - 37 ℃)) = 0.0310 Cal / (G ℃)

Men ettersom en kalori tilsvarer 4.1813 J, kan resultatet også uttrykkes som

cp = 0.130 J / (G ℃)

Referanser

1. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6^th. Ed. Prentice Hall. 400 - 410.
2. Kirkpatrick, l. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage Learning. 156 - 164.
3. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. Revidert utgave. McGraw Hill. 350 - 368.
4. Rex, a. 2011. Fundamentals of Physics. Pearson. 309 - 332.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14^th. Volum1. 556 - 553.
6. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9^na Cengage Learning. 362 - 374.