Vektor beløp

Hva er vektorbeløp?

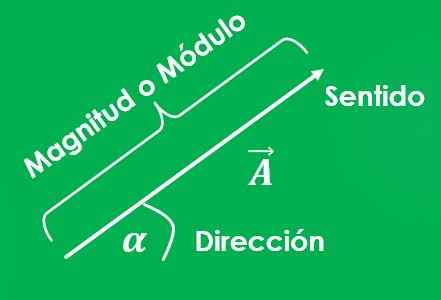
De Vektor mengde, eller vektor, som en som det er nødvendig å spesifisere både størrelsen eller modulen (med de respektive enhetene) og deres adresse.

I motsetning til vektormengden, har en skalær mengde bare størrelsesorden (og enheter), men ikke adresserer. Noen eksempler på skalare mengder er temperaturen, volumet til et objekt, lengden, massen og tiden, blant andre.

Forskjell mellom vektormengde og klatring

I det følgende eksemplet kan du lære å skille en skalær mengde fra en vektormengde:

En hastighet på 10 km/t er en skalær mengde, mens en hastighet på 10 km/t mot nord er en vektormengde. Forskjellen er at i det andre tilfellet er en adresse spesifisert, i tillegg til størrelsen.

Vektormengder har en uendelig applikasjoner, spesielt i fysikkens verden.

Grafikk og betegnelser av en vektormengde

Måten å betegne et vektorbeløp er ved å plassere en pil (→) på bokstaven som skal brukes, eller skrive bokstaven med fet skrift (til).

For å tegne en vektormengde er et referansesystem nødvendig. I dette tilfellet vil det kartesiske planet bli brukt som referansesystem.

Grafen til en vektor er en linje hvis lengde representerer størrelsen; og vinkelen mellom nevnte linje og x -aksen, målt i anti -Horary Sense, representerer adressen.

Det må spesifiseres hva utgangspunktet for vektoren er og hva som er ankomstpunktet. En pil er også plassert på slutten av linjen som peker på ankomstpunktet, noe som indikerer hva vektorens retning er.

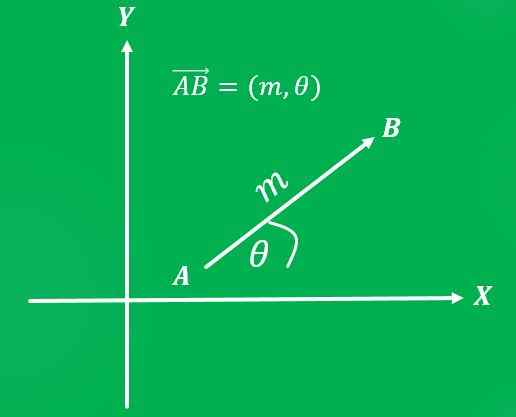
Når et referansesystem er angitt, kan du skrive vektoren som et ordnet par: den første koordinaten representerer sin størrelse og den andre koordinaten sin adresse.

Eksempler på vektorbeløp

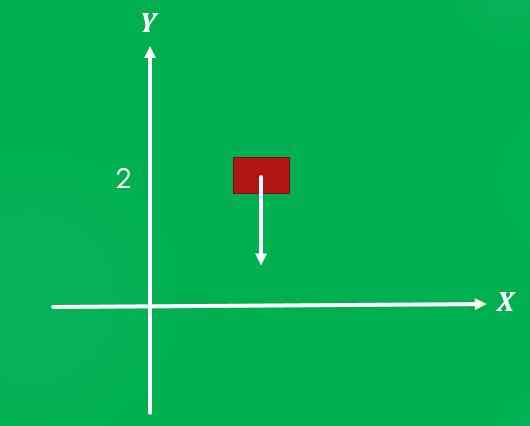
1- Tyngdekraft som virker på et objekt

Hvis et objekt er plassert i en høyde av 2 meter over bakken og det frigjøres, virker tyngdekraften på den med en styrke på 9,8 m/s², og en retning vinkelrett på bakken i retning.

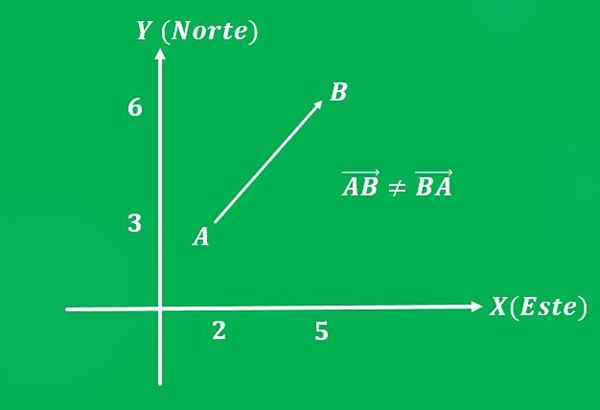
2- Bevegelse av et fly

Et fly som beveget seg fra punkt A = (2,3) til punkt B = (5,6) av det kartesiske planet, med en hastighet på 650 km/t (størrelsesorden). Retningen på banen er 45 ° mot nordøst (som betyr).

Det skal bemerkes at hvis ordren er omgjort, så har vektoren samme størrelse og samme retning, men forskjellig betydning, som vil være sørvest.

3- kraft påført et objekt

Juan bestemmer seg for å skyve en stol med en styrke på 10 pund, i en retning parallelt med bakken. De mulige sansene for den påførte kraften er: til venstre eller høyre (i tilfelle av det kartesiske planet).

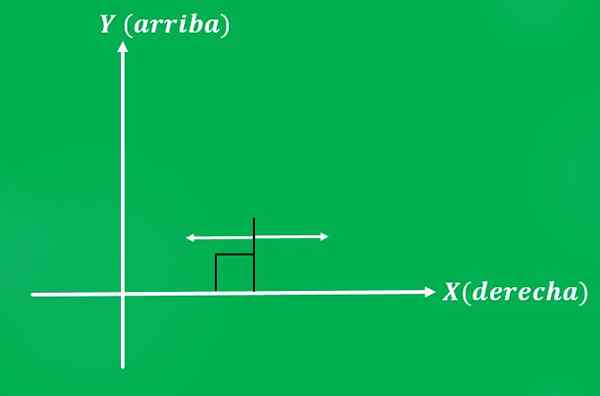
Så vel som i forrige eksempel, betydningen som Juan bestemmer seg for å gi styrken vil gi et annet resultat.

Dette forteller oss at to vektorer kan ha samme størrelse og retning, men være annerledes (gi forskjellige resultater).

To eller flere vektorer kan legges til og trekkes fra, som det er veldig nyttige resultater for, for eksempel parallellogramloven. Du kan også multiplisere en vektor med en skalar.