Kapasitansenheter, formler, beregning, eksempler

De Kapasitans Det er forholdet mellom belastningen til en kondensator eller trener, målt i Coulomb, og dens elektriske potensial eller spenning, målt i volt. Det kommer til uttrykk i Faradio (F) enheter, til ære for Michael Faraday (1791-1867).

Kapasitans er også definert som egenskapen eller kapasiteten til en kondensator eller sett med elektriske kondensatorer, som måles med mengden elektrisk ladning som kan lagres, separat, per endring av det elektriske potensialet.

Lampene, så vel som alle andre elektriske apparater, må en del av driften til kapasitans. Kilde: Pixabay.

Begrepet kapasitans introduseres som et resultat av opprettelsen av en elektrisk enhet kalt kondensatoren, oppfunnet av den prøyssiske forskeren Ewald Georg von Kleist, i 1745, og uavhengig av den nederlandske fysikeren Pieter Van Musschenbroek.

Kondensatorer er elektriske enheter som lagrer elektrisk lading og laster ned den øyeblikkelig. Denne egenskapen har blitt brukt i en rekke elektriske enheter, for eksempel TV, radio, lamper, datamaskin, blant mange andre i hverdagen.

[TOC]

Kondensator og kapasitans

En kondensator eller kondensator består av to drivere som har like belastning og ellers. Drivere kalles rustnings rustning eller kondensatorplater.

En plakett er knyttet til den positive (+) terminalen til ett batteri, mens den andre platen er koblet til det negative (-). Ettersom platene har like belastninger og det motsatte tegnet, er nettlasten til en kondensator null (0).

Kapasitans er forholdet mellom belastningen til en driver eller ledere som danner en kondensator og verdien av spenningsforskjellen mellom kondensatorplatene.

Kan tjene deg: Rosario kjølemedium

Enheter og formler

Kapasitansformelen er som følger:

C = Q / V

Hvor C er kapasitans, q belastningen (hvis enhet er Coulomb) og v  Spenningen (volt)

Kapasitansenheten er Faradio (F), som tilsvarer Coulomb / Voltio. Faradio er en veldig stor enhet, så mikrofradium (µF) brukes, tilsvarer 10^-6 Farad; eller Faradio Peak (PF), som tilsvarer 10^-12 Farad.

Hvordan beregnes kapasitans?

Det som vil være kapasitansverdien til en kondensator hvis plater har en belastning på 5 · 10^-3 Coulomb, og en 6 volt spenningsforskjell?

Bruke formelen vi løser:

C = Q / V

= (5 · 10^-3 Coulomb) / (6 volt)

= 8,33 · 10^-4  Farad

Eksempler

Kapasitansformelen varierer avhengig av type kondensator.

Parallelle plater kondensator

C = kε_entenA / d

k er den dielektriske konstanten, som har en verdi på 1 i luften og tomrommet. Av denne grunn reduseres formelen til:

C = ε_entenA / d

ε_enten Det er den dielektriske konstanten, hvis verdi er nær 8 854 · 10^-12 F · m^-1, A er området eller overflaten til de parallelle platene uttrykt i m², samtidig som d Avstanden som skiller parallelle plater.

Sfærisk kondensator

C = 4πε_entenR

Hvor r er radius for sfæren i meter.

Konsentriske kuler

C = 4πε_enten / (1/ r₁ - 1/r₂)

Konsentrisk sylinderkondensator

C = 2πε_entenl/ln (r₂ / R₁)

Hvor l er lengden på konsentriske sylindere i meter.

Løste øvelser

Parallelle flate plater kondensator

Det som vil være kapasiteten til en kondensator eller kondensator i luften med et område på sine 3 cm plater² og atskilt med en avstand på 2 mm?

Kan tjene deg: 12 eksempler på kjemiske baser

Vi har formelen:

C = ε_entenA/d

Og dataene:

ε_enten = 8.854 x 10^-12 F · m^-1

A = 3 cm² (3 · 10^-4 m²)

D = 2 mm (2 · 10^-3 m)

Fortsett å erstatte:

C = (8 854 · 10^-12 F · m^-1) (3 · 10^-4 m²) / (2 · 10^-3 m)

= 1.3281 · 10^-14 F

Kondensator eller sfære -formet kondensator

Hvis jorden blir betraktet som en sfærisk kondensator med en radius (r) på 6.370 km: Hva vil være verdien av din kapasitans?

Data:

C = 4πε_entenR

Π = 3.1416

ε_enten = 8 854 · 10^-12 F.m^-1

R = 6.370 km (6,37 · 10⁶ m)

Verdiene i kapasitansformelen erstattes igjen:

C = (4 · 3,1416) (8 854 · 10^-12 F · m^-1) (6.37 · 10⁶ m)

= 7.09 · 10^-8 F

= 709 µF

Kombinasjon av kondensatorer

Kondensatorer eller kondensatorer kan kombineres i serie eller parallelt.

Seriekondensatorer

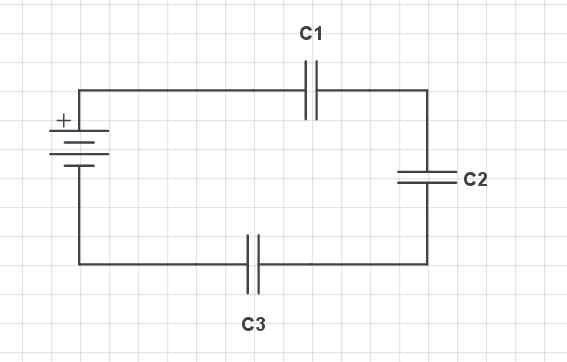Seriekondensatorer. Gabriel Bolívar Kilde via Circuitlab

Det øvre bildet viser tre seriekondensatorer (C₁, C₂ og c₃), samt et batteri med sine positive (+) og negative (-) terminaler. Disse kondensatorene har en serie egenskaper i forhold til spenning, belastning og kapasitans.

Spenningsdråpe (ΔV) i kondensatorer

ΔV_t = ΔV₁   +   ΔV₂   +    ΔV₃

Det totale spenningsfallet i et sett med serielle kondensatorer er lik summen av spenningsfallene til kondensatorene.

Byrde  av kondensatorer

Q_t = Q₁ = Q₂ = Q₃

Den samme mengden belastning sirkulerer gjennom serien.

Kondensatorer Kondensans

Den tilsvarende kapasitansen til serielle kondensatorer presenterer følgende forhold:

1 c_Eq  = 1/c₁  +   1 c₂   +   1 c₃

Parallelle kondensatorer

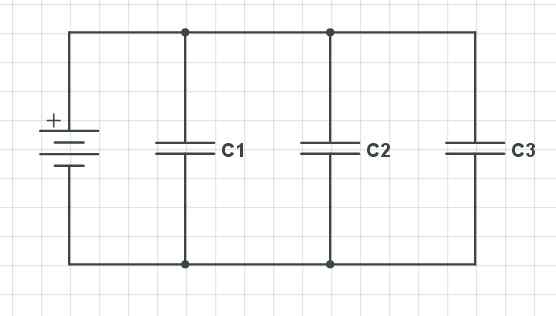Parallelle kondensatorer. Gabriel Bolívar Kilde via Circuitlab.

Opp har vi tre kondensatorer anordnet parallelt (C₁, C₂ og c₃), som holder i forhold til spenningsfall, belastning og kapasitans følgende oppførsel:

Kan tjene deg: Alkenes

Spenningsfall i kondensatorer

ΔV_t  = ΔV₁  = ΔV₂  = ΔV₃

I parallelle kondensatorer er det totale spenningsfallet i kondensatorer det samme som det eksisterende for hver av kondensatorene.

Kondensatorer

Q_t  = Q₁  +  Q₂  +  Q₃

I et system parallelt er den totale belastningen av kondensatorene lik summen av belastningen på alle kondensatorer.

Kondensatorer Kondensans

C_Eq  = C₁  +  C₂   +  C₃

I et parallelt system er den ekvivalente kapasitansen til dem lik summen av kapasitansene til alle kondensatorer.

Eksempel på en øvelse

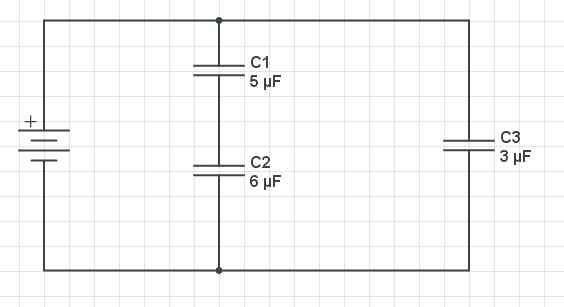Eksempel på et problem og parallelle kondensatorproblem. Gabriel Bolívar Kilde via Circuitlab.

Et skjema med tre kondensatorer er vist ovenfor: C₁ og c₂ De er ordnet i serie, og de er parallelle med C₃. Kondensatorens kapasitans er følgende: C₁ = 5 µF, C₂ = 6 µF og C₃ = 3 µF. Finn den tilsvarende kapasitansen til kretsen.

Først er den tilsvarende kapasitansen til C₁ og c₂ som er i serie.

1 c_Eq1,2 = 1/c₁  +  1 c₂

1 c_Eq1,2 = 1/5 µF +1/6 µF

1 c_Eq1,2 = (11/30) µF

C_Eq1,2 = 30 µF / 11

= 2,72 µF

Kondensatorer 1 og 2 er parallelt med C₃. Så den tilsvarende kapasitansen til C₁, C₂ og c₃ er lik C_Eq1,2 +  C₃.

C_Eq1,2,3 = 2,72 µF +3 µF

= 5,72 µF

Referanser

1. Serway, r. TIL. og Jewett, J. W. (2009). Fysikk for vitenskap og ingeniørfag. Volum 2. Syvende utgave. Redaksjonell Cengage Learning.
2. Reddick, R og Halliday, D. (1965). Fysisk.  Del 2. Andre utgave på spansk. Kontinental redaksjon s.TIL.
3. Studere. (22. april 2015). Kapasitans: enheter og formel. Gjenopprettet fra: Studie.com
4. Lumes fysikk. (s.F.). Kondensatorer i serie og parallell. Gjenopprettet fra: kurs.Lumenarning.com
5. Redaktørene av Enyclopaedia Britannica. (2020). Kapasitans. Gjenopprettet fra: Britannica.com