Chi-square (²) distribusjon, hvordan den beregnes, eksempler

Beviset Chi kvadrater enten Ji-square (χ², Hvor χ er det greske bokstaven kalt "chi") brukes til å bestemme oppførselen til en viss variabel, og også når du vil vite om to eller flere variabler er statistisk uavhengige.

For å sjekke oppførselen til en variabel, er testen som skal kalles Chi Square Test of Justering. Å vite om to eller flere variabler er statistisk uavhengig av testen kalles Chi Square of Independence, også kalt av beredskap.

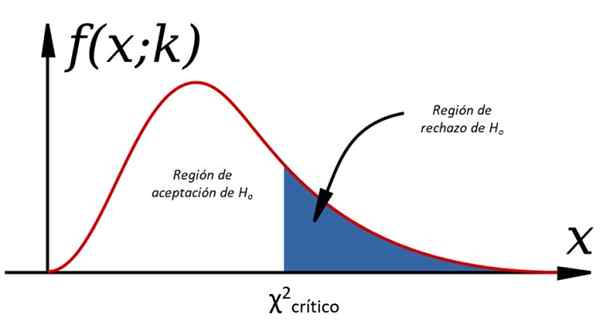
Figur 1. Hypotesetester via Chi Cuadrado

Disse bevisene er en del av den statistiske teorien om beslutninger, der en befolkning studeres og beslutninger tas om den, og analyserer en eller flere prøver hentet fra den. For dette er det nødvendig å gjøre visse forutsetninger angående variablene, kalt hypotese, som kanskje ikke er sikker.

Det er noen tester for å kontrastere disse formodningene og bestemme hvilke som er gyldige, innenfor en viss konfidensmargin, inkludert chi-square-testen, som kan brukes for å sammenligne to og de fleste populasjoner.

Som vi vil se, vurderes vanligvis to typer hypotese om noen populasjonsparameter i to prøver: nullhypotesen, kalt h_enten (Prøvene er uavhengige), og den alternative hypotesen, betegnet som h₁, (Prøvene er korrelert) som er i strid med det.

[TOC]

Når brukes chi-square-testen?

Chi Square -testen gjelder variabler som beskriver egenskaper, for eksempel sex, sivil status, blodgruppe, øyenfarge og preferanser av forskjellige typer.

Testen er designet når det er ønsket:

-Sjekk om en distribusjon er passende for å beskrive en variabel, som kalles justering godhet. Gjennom Chi Square -testen kan du vite om det er signifikante forskjeller mellom den valgte teoretiske fordelingen og frekvensfordelingen observert.

-Vet om to X- og Y -variabler er uavhengige av det statistiske synspunktet. Dette er kjent som Uavhengighetstest.

Siden det gjelder kvalitative eller kategoriske variabler, er Chi Square -testen mye brukt i samfunnsvitenskap, administrasjon og medisin.

Betingelser for å anvende det

Det er to viktige krav for å bruke det riktig:

Det kan tjene deg: Hva er forholdet mellom Rhombus -området og rektangelet?

-Dataene må grupperes i frekvenser.

-Utvalget må være stor nok til å gjøre Chi Square -distribusjonen gyldig, ellers blir verdien overvurdert og gir opphav til avvisning av nullhypotesen når den ikke skal være slik.

Den generelle regelen er at hvis den ikke brukes i grupperte data med verdi mindre enn 5. Hvis det er mer enn en frekvens mindre enn 5, må de kombineres i en for å oppnå en frekvens med numerisk verdi større enn 5.

Chi Square Distribution

χ² Det er en kontinuerlig fordeling av sannsynligheter. Det er faktisk forskjellige kurver, avhengig av en parameter k kalt grader av frihet tilfeldig.

Egenskapene er:

-Området under kurven er lik 1.

-Verdiene til χ² De er positive.

-Fordelingen er asymmetrisk, det vil si at den har skjevhet.

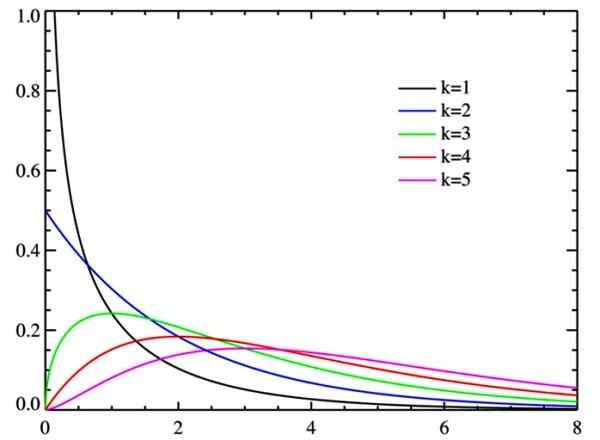Figur 2. Chi Square Distribution for Watts grader of Freedom. Kilde: Wikimedia Commons.

Grader av frihet

Når frihetsgradene øker, har chi-square-fordelingen en tendens til normal, som det kan sees på figuren.

For en gitt distribusjon bestemmes frihetsgrader gjennom beredskapstabell, som er tabellen der de observerte frekvensene til variablene blir registrert.

Hvis et bord har F rangering og c kolonner, verdien av k er:

K = (f - 1) ⋅ (c - 1)

Hypoteseformulering

Når Chi Square -testen er justering, formuleres følgende hypoteser:

-H_enten: variabel x har sannsynlighetsfordeling f (x) med spesifikke parametere og₁, og₂..., og_p

-H₁: X har en annen sannsynlighetsfordeling.

Sannsynlighetsfordelingen som antas i nullhypotesen kan for eksempel være den velkjente normalfordelingen, og parametrene vil være gjennomsnittlig μ og standardavviket σ.

I tillegg blir nullhypotesen evaluert med et visst nivå av betydning, det vil si et mål på feilen som vil bli gjort når du avviser det å være sant.

Generelt er dette nivået etablert på 1 %, 5 % eller 10 % og jo lavere testresultatet, desto mer pålitelig.

Kan tjene deg: Mamma

Og hvis Chi Square -testen av beredskap brukes, som som vi har sagt tjener til å bekrefte uavhengigheten mellom to variabler x og y, er hypotesene:

-H_enten: Variablene X og Y er uavhengige.

-H₁: X og y er avhengige.

Igjen er det nødvendig å spesifisere et nivå av betydning for å vite målet for feilen når du tar avgjørelsen.

Hvordan beregnes chi-square statistikk?

Chi Square -statistikk beregnes som følger:

Symbolet ∑ betyr "summering", som vi må lage om det indikerte brøkuttrykket.

Summen utføres fra første klasse I = 1 til den siste, som er i = k.

I tillegg:

-F_enten Det er en observert frekvens (den kommer fra dataene som er oppnådd).

-F_og Det er forventet eller teoretisk frekvens (det er nødvendig å beregne den fra dataene).

For å akseptere eller avvise nullhypotesen, beregnes χ² For observerte data og sammenligner med en verdi som kalles Chi Critical Square, som avhenger av frihetsgrader k og nivået av betydning α:

χ²_kritisk =  χ²_{K, α}

Hvis vi for eksempel ønsker å utføre testen med et signifikansnivå på 1 %, så α = 0.01, hvis det vil være med 5%, så α = 0.05 og så videre. P, distribusjonsparameteren, for eksempel:

P = 1 - α

Disse kritiske kvadratverdiene bestemmes av tabeller som inneholder verdien av det akkumulerte området. For eksempel for k = 1, som representerer 1 grad av frihet og α = 0.05, tilsvarer p = 1-.05 = 0.95, verdien av χ² Det er 3.841.

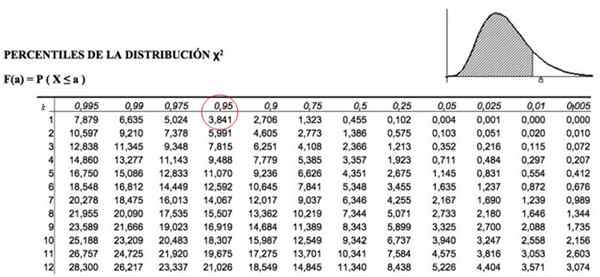Figur 3. Chi Square Distribution Verditabell. Kilde: f. Zapata.

AC akseptkriterier_enten

Kriteriene for å akseptere h_enten er:

-Ja χ² < χ²_kritisk  H_enten, Ellers blir den avvist (se figur 1).

Eksempel på beregning

I følgende applikasjon vil Chi Square -testen bli brukt som en uavhengighetstest.

Anta at forskere vil vite om preferansen for svart kaffe er relatert til personens sjanger, og spesifiser svaret med et nivå av betydning av α = 0.05.

Kan tjene deg: eksterne alternative vinkler: øvelser og øvelser løst

For dette er et utvalg på 100 personer som er intervjuet og svarene deres tilgjengelige:

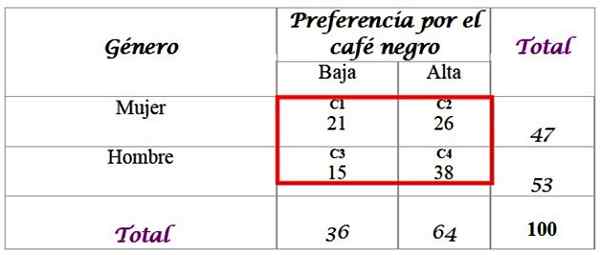
Trinn 1

Etablere hypoteser:

-H_enten: Kjønn og preferanse for svart kaffe er uavhengige.
-H₁: Smaken for svart kaffe er relatert til personens sjanger.

Steg 2

Beregn de forventede frekvensene for distribusjon, som totalen ble lagt til i den siste raden og i høyre -wing -kolonnen er nødvendig. Hver celle i den røde boksen har en forventet verdi F_og, som beregnes ved å multiplisere totalen av R -rad F med den totale kolonnen C, delt med den totale prøven n:

F_og = (F x c) /n

Resultatene er som følger for hver celle:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Trinn 3

Da må du beregne Chi Cuadrado -statistikken for denne distribusjonen, i henhold til den gitte formelen:

χ²= [(21 - 16.92)² ÷ 16. 92] + [(26 - 30.08)² ÷ 30.08] + [(15 - 19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

Trinn 4

Bestem χ²_kritisk, Når du vet at de registrerte dataene er F = 2 rader og C = 2 kolonner, er antallet frihetsgrader:

K = (2-1) ⋅ (2-1) = 1.

Noe som betyr at vi må se i tabellen vist over verdien av χ²_{K, α} = χ²_{1; 0.05} , som er:

χ²_kritisk = 3.841

Trinn 5

Sammenlign verdiene og bestemme:

χ² = 2.9005

χ²_kritisk = 3.841

Siden χ² < χ²_kritisk Nullhypotesen aksepteres, og det konkluderes med at preferansen for svart kaffe ikke er knyttet til personens sjanger, med et signifikansnivå på 5%.

Referanser

1. Chi Square -test for uavhengighet. Gjenopprettet fra: Saylordotorg.Github.Io.
2. Med Wave. Statistikk anvendt på helsevitenskap: Ji-square-testen. Gjenopprettet fra: Medwave.Cl.
3. Sannsynligheter og statistikk. SHI Square Justering Goodness Test. Hentet fra: Sannsynligheter Andestics.com.
4. Triola, m. 2012. Elementær statistikk. 11. Utgave. Addison Wesley.
5. Unam. Chi Square Test. Gjenopprettet fra: Rådgivning.Cuautitlan2.Unam.MX.