Grupperte dataeksempler og løst trening

De grupperte data De er de som har klassifisert seg i kategorier eller klasser, og tar som kriterier sin frekvens. Dette gjøres med det formål å forenkle styringen av store datamengder og etablere sine trender.

Når de er organisert i disse klassene for frekvensene sine, utgjør dataene en Frekvensfordeling, fra hvilken verktøyinformasjon blir trukket ut gjennom sine egenskaper.

Figur 1. Med grupperte data kan du bygge grafikk og beregne statistiske parametere som beskriver trender. Kilde: Pixabay.

Neste gang vil vi se et enkelt eksempel på grupperte data:

Anta at staturen til 100 kvinnelige studenter, valgt fra alle grunnleggende fysikkurs ved et universitet, måles og følgende resultater oppnås:

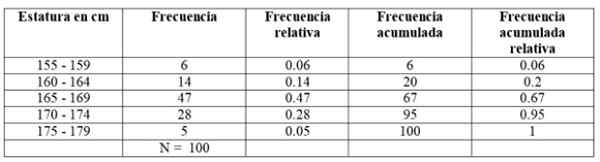
Resultatene som ble oppnådd ble delt inn i 5 klasser, som vises i venstre kolonne.

Den første klassen, mellom 155 og 159 cm, har 6 elever, andre klasse 160 - 164 cm har 14 elever, den tredje klassen fra 165 til 169 cm er den med det største antallet medlemmer: 47. Følg deretter klassen 170-174 cm med 28 studenter og til slutt den fra 175 til 179 cm med bare 5.

Antall medlemmer av hver klasse er nettopp Frekvens enten Absolutt fresuens Og ved å legge dem alle inn, oppnås de totale dataene, som i dette eksemplet er 100.

[TOC]

Frekvensfordelingsegenskaper

Frekvens

Som vi har sett, er frekvensen antall ganger et faktum gjentas. Og for å lette beregningene av distribusjonsegenskapene, for eksempel gjennomsnitt og varians, er følgende mengder definert:

-Akkumulert frekvens: Det oppnås ved å legge til frekvensen av en klasse med den fremre akkumulerte frekvensen. Den første av alle frekvensene sammenfaller med det aktuelle intervallet, og det siste er det totale antallet data.

-Relativ frekvens: Det beregnes ved å dele den absolutte frekvensen til hver klasse med det totale antallet data. Og hvis du multipliserer med 100, har du prosentvis frekvensprosent.

Kan tjene deg: vektorfunksjoner

-Akkumulert relativ frekvens: Det er summen av de relative frekvensene for hver klasse med den forrige akkumulerte. Den siste av de akkumulerte relative frekvensene må være lik 1.

For vårt eksempel er frekvensene slik:

Grenser

De ekstreme verdiene for hver klasse eller intervall kalles Klassegrenser. Som vi ser har hver klasse en nedre grense og en større. For eksempel har den første klassen i studien om statene en grense mindre enn 155 cm og en større enn 159 cm.

Dette eksemplet har grenser som er klart definert, men det er mulig.

Grenser

Høyde er en kontinuerlig variabel, så det kan vurderes at den første klassen faktisk begynner i 154.5 cm, siden ved avrunding av denne verdien til nærmeste heltall, oppnås 155 cm.

Denne klassen dekker alle verdier opp til 159.5 cm, fordi fra dette er statene avrundet til 160.0 cm. En status på 159.7 cm tilhører allerede neste klasse.

Den virkelige klassegrensene for dette eksemplet er, i CM:

• 154.5 - 159.5
• 159.5 - 164.5
• 164.5 - 169.5
• 169.5 - 174.5
• 174.5 - 179.5

Amplitude

Bredden i en klasse oppnås ved å trekke fra grensene. For det første intervallet i vårt eksempel har du 159.5 - 154.5 cm = 5 cm.

Leseren kan bekrefte at for de andre intervallene i eksemplet er amplituden også resultatet av 5 cm. Imidlertid er det bemerkelsesverdig at distribusjoner kan bygges med intervaller med forskjellig amplitude.

Det kan tjene deg: Regel T: Karakteristikker, slik at det er eksempler

Klassemerke

Det er intervallet med middels punkt og oppnås med gjennomsnittet mellom den øvre grensen og den nedre grensen.

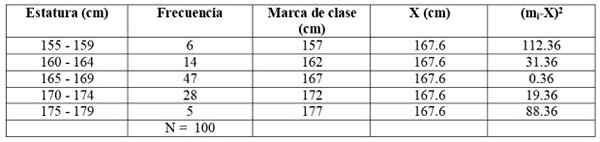
For vårt eksempel er merkevaren First Class (155 + 159)/2 = 157 cm. Leseren kan bekrefte at de gjenværende klassemerkene er: 162, 167, 172 og 177 cm.

Det er viktig å bestemme klassemerker.

Målinger av sentral tendens og spredning for grupperte data

De mest brukte sentrale tendensstiltakene er gjennomsnittlige, median og mote, og beskriver nettopp tendensen til dataene som skal grupperes rundt en viss sentral verdi.

Halv

Det er en av de viktigste sentrale tendensstiltakene. I de grupperte dataene kan det aritmetiske gjennomsnittet beregnes ved å bruke formelen:

 Hvor:

-X er gjennomsnittet

-F_Yo er frekvensen av klassen

-m_Yo Det er klassemerket

-G er antall klasser

-n er det totale antallet data

Median

For medianen må du identifisere intervallet der observasjonen N/2 er lokalisert. I vårt eksempel er denne observasjonen nummer 50, fordi det er totalt 100 data. Denne observasjonen er i intervallet 165-169 cm.

Da må du interpolere for å finne den numeriske verdien som tilsvarer den observasjonen, som formelen brukes til:

Hvor:

-C = intervallbredde der medianen er lokalisert

-B_M = Den nedre grensen til intervallet som medianen tilhører

-F_m = mengden observasjoner inneholdt i medianintervallet

-N/2 = Halvparten av de totale dataene

-F_BM = Totalt antall observasjoner før medianintervallet

Mote

For mote er modalklassen identifisert, den som inneholder de fleste observasjoner, hvis klassemerke er kjent.

Kan tjene deg: sekskantet pyramide

Varians og standardavvik

Varians og standardavvik er spredningstiltak. Hvis vi betegner variansen med S² Og til standardavviket, som er kvadratroten til variansen som s, for grupperte data vil vi ha henholdsvis:

OG

Trening løst

For distribusjon av status av universitetsstudenter som er foreslått i begynnelsen, beregner du verdiene til:

a) Gjennomsnitt

b) Medium

c) Mote

d) Varians og standardavvik.

Figur 2. Når det gjelder mange verdier, for eksempel staten til en stor gruppe studenter, er det å foretrekke å gruppere dataene i klasser. Kilde: Pixabay.

Løsning på

La oss bygge følgende tabell for å lette beregninger:

Gjennom uttrykket for den gjennomsnittlige gruppen gruppert ovenfor:

Erstatte verdier og utføre summen direkte:

X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) /100 cm =

= 167.6 cm

Løsning b

Intervallet som medianen tilhører er 165-169 cm fordi det er intervallet hyppigst.

La oss identifisere hver av disse verdiene i eksemplet, ved hjelp av tabell 2:

C = 5 cm (se Amplitude -delen)

B_M = 164.5 cm

F_m = 47

N/2 = 100/2 = 50

F_BM = 20

Erstatte i formelen:

Løsning c

Intervallet som er inneholdt i de fleste observasjoner er 165-169 cm, hvis klassemerke er 167 cm.

Løsning d

Vi utvider forrige tabell ved å legge til ytterligere to kolonner:

Vi bruker formelen:

Og vi utvikler summen:

s² = (6 x 112.36 + 14 x 31.36 + 47 x 0.36 + 28 x 19.36 + 5 x 88.36) / 99 = = 21.35 cm²

Derfor:

S = √21.35 cm² = 4.6 cm

Referanser

1. Berenson, m. 1985. Statistikk for administrasjon og økonomi. Inter -American s.TIL.
2. Canavos, g. 1988. Sannsynlighet og statistikk: applikasjoner og metoder. McGraw Hill.
3. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
4. Levin, r. 1988. Statistikk for administratorer. 2. Utgave. Prentice Hall.
5. Spiegel, m. 2009. Statistikk. Schaum -serien. 4 ta. Utgave. McGraw Hill.
6. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.