Hvordan få vinkelen på en trekant? (Eksempel)

Det er forskjellige måter å Beregn sidene og vinklene til en trekant. Disse er avhengige av hvilken type trekant du jobber med.

Ved denne anledningen vil det bli vist hvordan du kan beregne sidene og vinklene til en høyre trekant, forutsatt at visse trekantdata med bekjente med bekjente.

Elementene som skal brukes er:

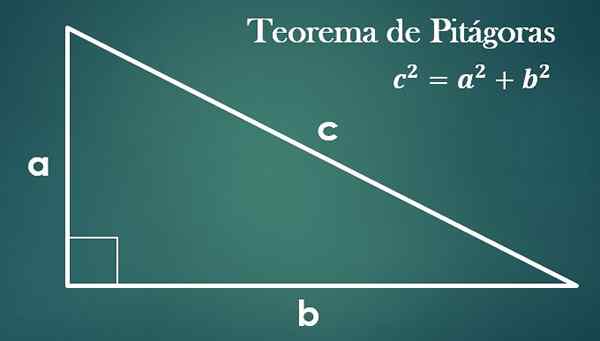
- Pythagoras teorem

Gitt en rektangel -trekant med "A", "B" og hypotenusa "C", er det sant at "C² = A²+B²".

- Område av en trekant

Formelen for beregning av området til en hvilken som helst trekant er A = (B × H)/2, der "B" er lengden på basen og "H" lengden på høyden.

- Vinkler på en trekant

Summen av de tre indre vinklene til en trekant er 180 °.

- Trigonometriske funksjoner:

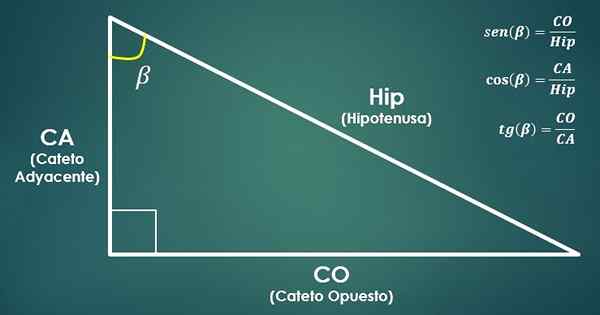
Tenk på en riktig trekant. Deretter er de trigonometriske funksjonene definert sinus, kosinus og tangent av beta -vinkelen (β) som følger:

Sin (β) = CO/Hyp, Cos (β) = Ca/hofte og solbrun (β) = CO/Ca.

Hvordan beregne sidene og vinklene til en høyre trekant?

Gitt en ABC Rectangle -trekant, kan følgende situasjoner presenteres:

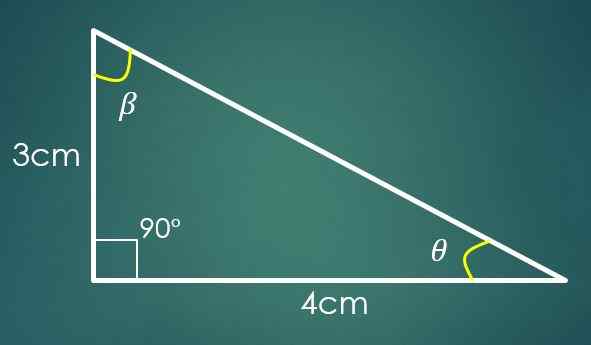
1- De to bena er kjent

Hvis katetoen "A" måler 3 cm og kateto "B" måler 4 cm, for å beregne verdien av "C" brukes Pythagoras -teoremet. Ved å erstatte verdiene til "A" og "B" oppnås det at C² = 25 cm², noe som innebærer at C = 5 cm.

Nå, hvis vinkelen β er motsatt av kategorien "B", så er Sin (β) = 4/5. Ved bruk av brystfunksjonen til brystet, oppnås det i denne siste likheten at β = 53,13º. To indre vinkler på trekanten er allerede kjent.

La θ være vinkelen som gjenstår å være kjent, deretter 90º+53,13º+θ = 180 °, hvor det oppnås at θ = 36,87º.

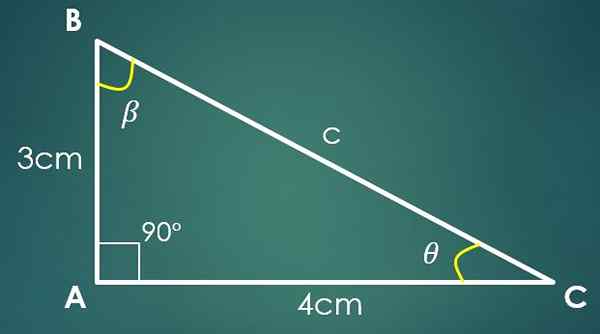
I dette tilfellet er det ikke nødvendig at de kjente sidene er de to bena, er det viktige å vite verdien av to sider.

2- Et ben og området er kjent

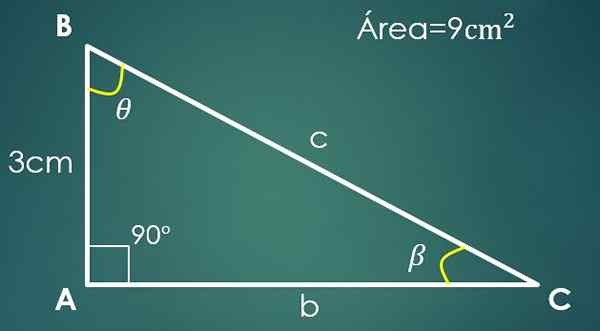
La A = 3 cm det kjente benet og 9 cm² trekantområdet.

I et rektangel -trekant kan en kategori betraktes som base og den andre som høyde (siden de er vinkelrett).

Anta at "A" er basen, derfor 9 = (3 × h)/2, der det oppnås at den andre kategorien måler 6 cm. For å beregne hypotenusen, fortsett som i forrige tilfelle, og det oppnås at C = √45 cm.

Nå, hvis vinkelen β er motsatt av "A" -kateto, så er Sin (β) = 3/√45. Ved rydding β oppnås det at verdien er 26,57º. Du trenger bare å vite verdien av den tredje vinkelen θ.

Det er oppfylt at 90 °+26,57º+θ = 180 °, der det konkluderes med at θ = 63,43º º.

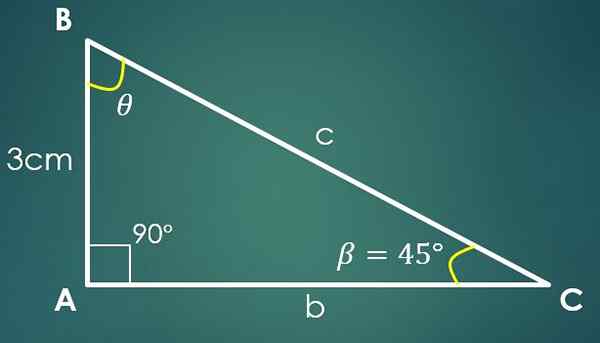
3- En vinkel og en kateto er kjent

La β = 45 ° den kjente vinkelen og A = 3 cm det kjente benet, der kateto “a” er imot vinkelen β. Ved hjelp av tangentformelen oppnås det at Tg (45 °) = 3/Ca, der det viser seg at Ca = 3 cm.

Ved hjelp av Pythagoras teorem oppnås det at C² = 18 cm², det vil si C = 3√2 cm.

Det er kjent at en vinkel måler 90 ° og at β måler 45 °, herfra konkluderes det med at den tredje vinkelen måler 45 °.

I dette tilfellet trenger ikke den kjente siden å være et ben, det kan være noen av de tre sidene av trekanten.