Balanseforhold konsept, applikasjoner og eksempler

De likevektsforhold De er nødvendige for at en kropp skal forbli i ro eller i ensartet rettlinjet bevegelse. I det første tilfellet sies det at objektet er i statisk likevekt, mens det i det andre er i dynamisk likevekt.

Forutsatt at det mobile objektet er en partikkel, i hvilket tilfelle dimensjonene ikke blir tatt i betraktning, er det nok at summen av krefter som virker på den er annullert.

Figur 1. Brimhams bergarter nord for England oppfyller likevektsforholdene. Kilde: Public Domain fartures.nett.

Men et stort flertall av mobile objekter har betydelige dimensjoner, derfor er ikke denne tilstanden nok til å garantere balanse, som i alle fall er fraværet av akselerasjon, ikke av bevegelse.

[TOC]

Første og andre likevektstilstand

La oss se: Hvis summen av krefter er ugyldig, er det sant at objektet ikke kommer til å bevege seg eller bevege seg raskt, men det kan fortsatt begynne å snu.

Derfor, for å unngå rotasjoner, må en annen tilstand.

Kort sagt, og betegner hvordan F Nettokraften og τ enten M Til nettmomentvektoren vil vi ha:

Første balansetilstand

∑ F = 0

Som betyr at: ∑ f_x = 0, ∑ f_og = 0 og ∑ f_z = 0

Andre likevektstilstand

∑ τ = 0 eller ∑ M = 0

Med dreiemomenter eller øyeblikk beregnet med hensyn til et hvilket som helst punkt.

I det følgende vil vi anta at det mobile objektet er en stiv kropp, en som ikke opplever noen deformasjon.

applikasjoner

Selv om bevegelsen ser ut til å være fellesnevneren i universet, er balansen også til stede i mange aspekter av naturen og i gjenstandene som omgir oss.

Kan tjene deg: Millikan Eksperiment: Prosedyre, forklaring, betydning

Isostatisk balanse

I en planetarisk skala er jorden i isostatisk balanse, En slags gravitasjonsbalanse av jordskorpen, hvis tetthet ikke er ensartet.

Forskjellene i tetthetene til de forskjellige blokkene eller områdene i jordskorpen kompenseres med høydeforskjellene som kjennetegner orografien til planeten. Det fungerer på samme måte som forskjellige materialer senker mer eller mindre i vann i henhold til deres tetthet og når balanse.

Men siden barkblokkene ikke flyter i vann, men i mantelen, som er mye mer tyktflytende, kalles ikke balansen hydrostatisk, men isostatisk.

Fusjonsoperasjon i kjernen

I stjernene som sol. Vi er avhengige av denne balansen slik at jorden får nødvendig lys og varme.

Konstruksjon

I lokal skala ønsker vi at bygninger og konstruksjoner skal forbli stabile, det vil si at likevektsforholdene overholder, spesielt den statiske balansen.

Det er grunnen til at statikken oppsto, som er grenen av mekanikk dedikert til å studere balansen i kroppene og alt som trengs for å holde dem slik.

Statiske likevektstyper

I praksis finner vi at statisk balanse kan være av tre klasser:

Stabil balanse

Det oppstår når objektet beveger seg fra sin posisjon og umiddelbart vender tilbake til den når kraften som flyttet den bort. Jo nærmere et objekt av jorda, jo mer sannsynlig er det nødvendig å være i stabil likevekt.

Kan tjene deg: tilsynelatende tetthet: formel, enheter og øvelser løst

Høyre -wing -ballen i figur 2 er et godt eksempel, hvis vi tar den ut av balanseposisjonen i bunnen av bollen, vil tyngdekraften være ansvarlig for raskt å returnere.

Likegyldig eller nøytral balanse

Det oppstår når objektet, til tross for at de blir flyttet, fortsetter i balanse. Runde gjenstander som ballen, når de er plassert på flate overflater, er i likegyldig balanse.

Ustabil balanse

Det oppstår når objektet beveger seg fra likevektsposisjonen, går ikke tilbake til den. Hvis vi holder ballen fra bakken til venstre, er det sikkert at den ikke vil komme tilbake på sine egne midler.

Figur 2. Balansetyper. Kilde: Wikimedia Commons.

Eksempel: Partikkelstatisk

Anta at en masseblokk m På et skrå plan, som antas å være konsentrert i dets geometriske sentrum.

Den horisontale komponenten i vekt w_x Det har en tendens til å få blokken til å gli ned, derfor en annen styrke som motsetter seg. Hvis vi vil at blokken skal holde seg i ro, er denne styrken statisk friksjon. Men hvis vi lar blokken gli nedoverbakke med konstant hastighet, er den nødvendige styrken dynamisk friksjon.

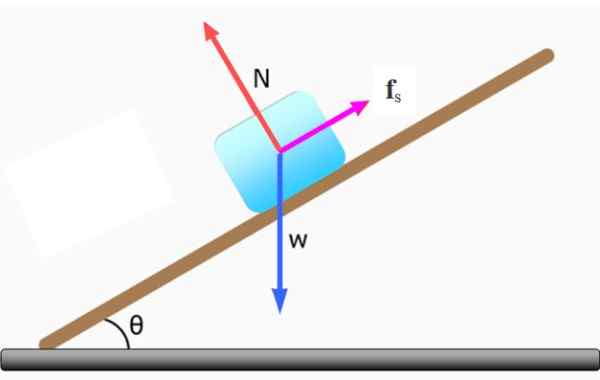Figur 3. En blokk forblir i statisk balanse på det skrå planet. Kilde: f. Zapata.

I mangel av friksjon vil blokken gli nede, og i så fall vil det ikke være noen balanse.

For at blokken skal være i ro, kreftene som virker på den: vekt W, Det normale N og statisk friksjon F_s, De må kompenseres. Så:

∑ f_og = 0 → N - W_og = 0

∑ f_x = 0 → w_x - F_s = 0

Statisk friksjon balanserer den horisontale komponenten i vekten: w_x = f_s og derfor:

F_s = m . g .sin θ

Trening løst

Et trafikklys på 21.5 kg henger fra en homogen AB -aluminiumsbar på 12 kg masse og 7.5 m langt, opprettholdt av et CD -horisontalt tau, som vist på figuren. Finne:

Kan tjene deg: Overleggsteorem: Forklaring, applikasjoner, løste øvelser

a) CD kabelspenning

b) De horisontale og vertikale komponentene i kraften utøvd av pivoten på innlegget.

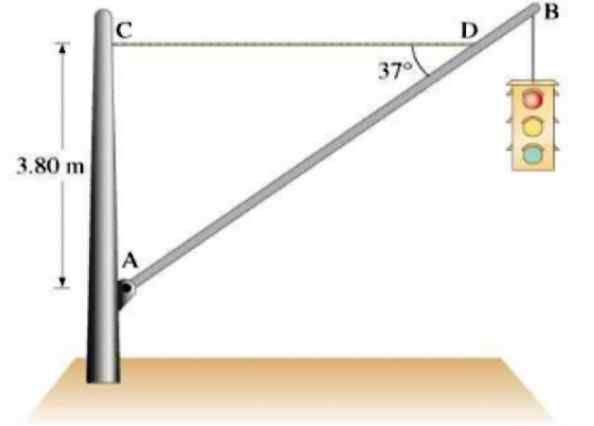Figur 4.- Et trafikklys henger fra en aluminiumsbar i statisk likevekt. Kilde: Giancoli. D. Fysikk med applikasjoner.

Løsning

Krefter -diagrammet som brukes på stangen er bygget, med vekten W, Spenningene i strengene og de horisontale og vertikale komponentene i pivotreaksjonen, kalt r_x og r_og. Da gjelder likevektsforholdene.

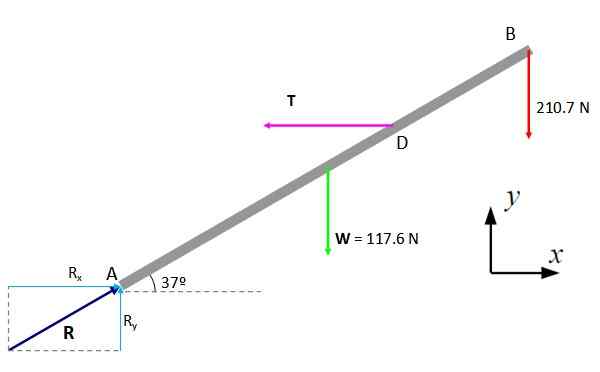Figur 5. Gratis kroppsdiagram for stangen. Kilde: f. Zapata.

Første tilstand

Å være et problem i flyet, tilbyr den første likevektstilstanden to ligninger:

Σf_x = 0
Σf_og = 0

Fra den første:

R_x - T = 0

R_x = T

Og av det andre:

R_og - 117.6 n - 210.7 n = 0

R_og = 328.3 n

Den horisontale komponenten i reaksjonen er av like stor størrelse som T -spenningen.

Andre tilstand

Punkt A i figur 5 er valgt som et svingesenter, på denne måten reaksjonsarmen R Det er ugyldig, husk at størrelsen på øyeblikket er gitt av:

M = f_┴ d

Hvor f_┴ Det er den vinkelrette komponenten i kraften og D er avstanden mellom rotasjonsaksen og påføringspunktet for kraften. Vi vil få en ligning:

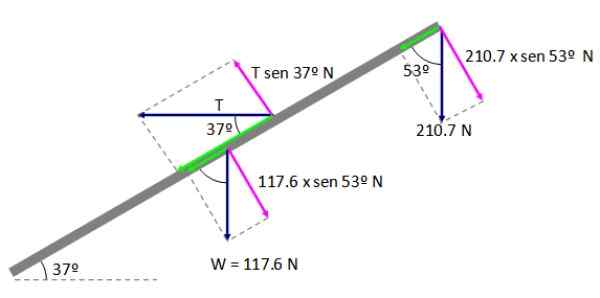Figur 6. Øyeblikk angående punkt a. Kilde: f. Zapata.

Σm_TIL = 0

(210.7 × Sen 53º) AB + (117.6 × Sen 53º) (AB/2) - (T × SEN 37º) AD = 0

Avstandsannonsen er:

AD = (3.8 m / sin 37º) = 6.3 m

(210.7 × sen 53º N) (7.5 m) + (117.6 × sen 53º N) (3.75 m) - (T × Sen 37º N) (6.3 m) = 0

Utføre de angitte operasjonene:

1262.04 + 352.20 - 3.8t = 0

Å rydde T får:

T = 424.8 n

Fra den første tilstanden måtte den_x = T, derfor:

R_x = 424.8 n

Temaer av interesse

Første balansetilstand.

Andre likevektstilstand.

Referanser

1. Bedford, 2000. TIL. Mekanikk for ingeniørfag: statisk. Addison Wesley.
2. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 4. Partikkelsystemer. Redigert av Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1.
5. Wikipedia. Isostasia. Gjenopprettet fra: er.Wikipedia.org.