Ledningsformler, beregning, eksempler, øvelser

De ledning Fra en sjåfør er det definert som lettheten den må savne den elektriske strømmen. Det avhenger ikke bare av materialet som brukes til produksjonen, men også av dets geometri: lengde og område av tverrsnittet.

Symbolet som brukes til konduktans er G, og er det omvendte elektriske motstanden R, en litt mer kjent størrelse. Den internasjonale systemenheten hvis for ledning er det omvendte av Ohmio, betegnet som ω^-1 og motta navnet på Siemens (S).

Figur 1. Konduktans avhenger av materialet og førerens geometri. Kilde: Pixabay.

Andre termer som brukes i elektrisitet, som høres ut som ledning og er relatert er Konduktivitet og kjøring, Men de skal ikke forveksles. Den første av disse begrepene er en iboende egenskap til stoffet som sjåføren er produsert, og den andre beskriver strømmen av elektrisk ladning gjennom den.

For en elektrisk leder med konstant tverrsnitt av området TIL, lengde L og konduktivitet σ, Konduktansen er gitt av:

G = σ.TIL

Til større konduktivitet, større konduktans. Dessuten, jo større korseseksjonsområde er, desto enklere er sjåføren til å la strømmen passere. Tvert imot, jo større lengde l, jo lavere konduktans, siden de nåværende transportørene mister mer energi på lengre reiser.

[TOC]

Hvordan beregnes konduktansen?

Konduktans G for en leder med et konstant tverrsnittsareal beregnes i henhold til ligningen gitt ovenfor. Dette er viktig, for hvis tverrsnittet ikke er konstant, må den integrerte beregningen brukes til å finne både motstand og konduktans.

Siden det er det omvendte motstanden, kan konduktansen G beregnes og vite at:

Kan tjene deg: kvantemekanisk modell av atomet

G = 1/r

Faktisk kan den elektriske motstanden til en driver måles direkte med et multimeter, et apparat som også måler strøm og spenning.

Drivere enheter

Som nevnt i begynnelsen, er konduktansenheten i det internasjonale systemet Siemens (e). Det sies at en sjåfør har en ledning på 1 s hvis strømmen som krysser den økes med 1 amperio for hver volt med potensiell forskjell.

La oss se hvordan det er mulig gjennom Ohms lov, hvis det er skrevet når det gjelder konduktans:

V = i.R = i/g

Hvor V Det er spenningen eller potensialforskjellen mellom endene på føreren og Yo Gjeldende intensitet. Når det gjelder disse størrelsene, forblir formelen slik:

G = i/v

Tidligere var enheten for ledning Mho (Ohm skrevet bakover) betegnet som ʊ, som er en hovedstad eller omvendt omega. Denne notasjonen ble brukt og ble erstattet av Siemens Til ære for den tyske ingeniøren og oppfinneren Ernst von Siemens (1816-1892), en pioner for telekommunikasjon, men begge er helt likeverdige.

1 MHO = 1 Siemens = 1 A/V (Ampere/Volt)

Figur 2. Konduktans versus motstand. Kilde: Wikimedia Commons. Tenk tank [CC med 3.0 (https: // creativecommons.Org/lisenser/av/3.0)]

I andre målesystemer Statsiemens (statistikk) (i CGS- eller centimeter-gram-sekundsystemet) og Absiemens (ABS) (Elektromagnetisk CGS -system) Med "S" på slutten, uten å indikere entall eller flertall, siden de kommer fra riktig navn.

Noen ekvivalenser

1 statistikk = 1.11265 x 10 ^-12 Siemens

1 abs = 1 x 10⁹ Siemens

Eksempler

Som nevnt før, med motstand, er konduktansen umiddelbart kjent når du bestemmer den omvendte eller gjensidige verdien. På denne måten tilsvarer en elektrisk motstand på 100 ohm.01 Siemens, for eksempel.

Under ytterligere to eksempler på ledningsbruk:

Kan tjene deg: magnetisk sjokk: enheter, formler, beregning, eksempler

Konduktivitet og konduktans

De er forskjellige vilkår, som allerede antydet. Konduktiviteten er en egenskap til stoffet som sjåføren er laget, mens sjåføren er typisk for sjåføren.

Konduktivitet kan uttrykkes i form av G som:

σ = g.(DE)

Deretter et bord med konduktiviteten til ofte brukte ledende materialer:

Tabell 1. Konduktivitet, resistiviteter og termisk koeffisient for noen ledere. Referansetemperatur: 20 ºC.

Metall	σ x 106 (Dere)	ρ x 10-8 (Ω.m)	α ºC-1
Sølv	62.9	1.59	0.0058
Kobber	56.5	1.77	0.0038
Gull	41.0	2.44	0.0034
Aluminium	35.4	2.82	0.0039
Wolfram	18.0	5.60	0.0045
Jern	10.0	10.0	0.0050

Motstand parallelt

Når de har kretsløp med parallelle motstander, er det noen ganger nødvendig å oppnå tilsvarende motstand. Å kjenne den tilsvarende motstandsverdien gjør det mulig å erstatte settet med motstand for en enkelt verdi.

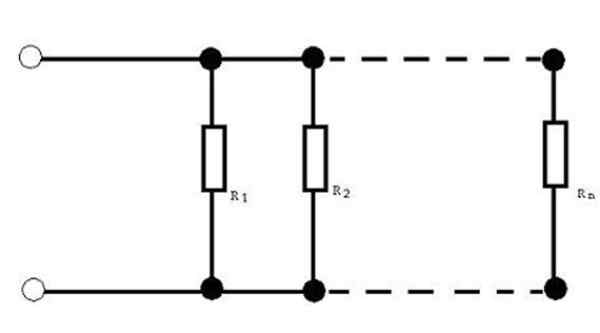Figur 3. Association of Resistances in parallel. Kilde: Wikimedia Commons. Ingen maskinlesbar forfatter gitt. Sotake antatt (basert på copyright -krav). [CC By-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/]].

For denne motstandskonfigurasjonen er den tilsvarende motstanden gitt av:

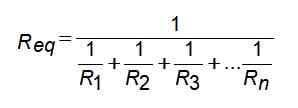
Men hvis du skriver når det gjelder konduktans, er det sterkt forenklet: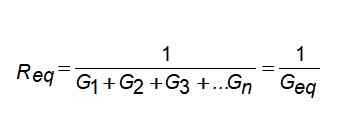Derfor:

G_Eq = G₁ + G₂ + G₃ +... g_n

Det vil si at tilsvarende konduktans er summen av konduktanser. Hvis du vil vite den tilsvarende motstanden, blir resultatet ganske enkelt investert.

Øvelser

- Oppgave 1

a) Skriv Ohms lov når det gjelder ledning.

b) Finn konduktansen til en 5 wolframtråd på 5.4 cm lang og 0.15 mm i diameter.

c) Nå blir en strøm på 1 bestått.5 A for ledningen. Hva er potensialforskjellen mellom endene på denne sjåføren?

Kan tjene deg: de 31 typene kraft i fysikk og deres egenskaper

Løsning på

Fra de foregående seksjonene må du:

V = i/g

G = σ.TIL

Erstatning av sistnevnte i det første, det forblir slik:

V = i /(σ.A/l) = i.L / σ.TIL

Hvor:

-Jeg er intensiteten til strømmen.

-L er førerlengden.

-σ er konduktivitet.

-A er området av tverrsnittet.

Løsning b

For å beregne konduktansen til denne wolframtråden, er dens konduktivitet nødvendig, som finnes i tabell 1:

σ = 18 x10⁶ Dere

L = 5.4 cm = 5.4 x 10^-2 m

D = 0. 15 mm = 0.15 x 10^-3 m

A = π.D² / 4 = π . (0.15 x 10^-3 m)² / 4 = 1.77 x 10^-8 m²

Erstatte i ligningen du har:

G = σ.A/l = 18 x10⁶ Dere . 1.77 x 10^-8 m² / 0.15 x 10^-3 M = 2120.6 s.

Løsning c

V = i/g = 1.5 A / 2120.6 s = 0.71 MV.

- Oppgave 2

Finn den tilsvarende motstanden i følgende krets og vite at jeg_enten = 2 a, beregne i_x og kraften spredt av kretsen:

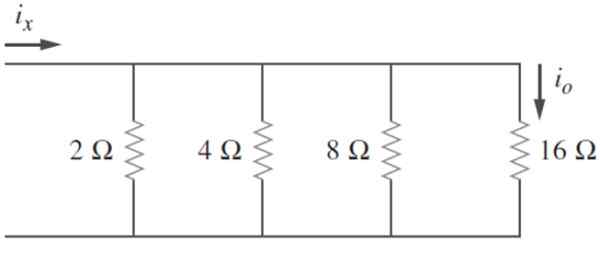Figur 4. Krets med parallelle motstander. Kilde: Alexander, C. 2006. Elektriske kretsfundamenter. 3. Utgave. McGraw Hill.

Løsning

Motstand er oppført: r₁= 2 Ω; R₂= 4 Ω; R₃= 8 Ω; R₄= 16 Ω

Konduktansen beregnes deretter i hvert tilfelle: g₁ = 0.5 ʊ; G₂ = 0.25 ʊ; G₃ = 0.125 ʊ; G₄ = 0.0625 ʊ

Og til slutt legger de opp som angitt før, for å finne den tilsvarende konduktansen:

G_Eq = G₁ + G₂ + G₃ +... g_n = 0.5 ʊ + 0.25 ʊ + 0.125 ʊ + 0.0625 ʊ = 0.9375 ʊ

Derfor r_Eq = 1.07 Ω.

Spenningen i r₄ er v₄ = jeg_enten. R₄ = 2 a . 16 Ω = 32 V, og er den samme for alle motstander, siden de er koblet sammen parallelt. Da er det mulig å finne strømningene som sirkulerer for hver motstand:

-Yo₁ = V₁ /R₁ = 32 V / 2 Ω = 16 a

-Yo₂ = V₂ /R₂ = 32 V / 4 Ω = 8 a

-Yo₃ = V₃ /R₃ = 32 V / 8 Ω = 4 a

-Yo_x = jeg₁ +  Yo₂ +  Yo₃ + Yo_enten = 16 + 8 + 4 + 2 a = 30 a

Endelig er den spredte kraften P:

P = (i_x)². R_Eq = 30 til x 1.07 Ω = 32.1 w

Referanser

1. Alexander, ca. 2006. Elektriske kretsfundamenter. 3. Utgave. McGraw Hill.
2. Megaamper / millivolt til Absiemens kalkulatorkonvertering. Gjenopprettet fra: Pinkbird.org.
3. Garcia, l. 2014. Elektromagnetisme. 2. Utgave. Industrial University of Santander. Colombia.
4. Knight, r.  2017. Fysikk for forskere og ingeniørfag: En strategitilnærming.  Pearson.
5. Roller, d. 1990. Fysisk. Elektrisitet, magnetisme og optikk. Volum II. Redaksjon tilbake.
6. Wikipedia. Elektrisk ledning. Gjenopprettet fra: er.Wikipedia.org.
7. Wikipedia. Siemens. Gjenopprettet fra: er.Wikipedia.org.