Ohm lov og formel, beregning, eksempler, øvelser

De Ohms lov, I sin makroskopiske form indikerer det at spenningen og intensiteten til strømmen i en krets er direkte proporsjonal, og motstanden er proporsjonalitetskonstanten. Ohms lov som betegner disse tre størrelsene som henholdsvis V, I og R, fastslår at: V = i.R.

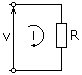
På samme måte er Ohms lov generalisert til å omfatte kretselementer som ikke er rent motstandsdyktige i vekselstrømskretser, og vedtar således som følger: V = i. Z.

Figur 1. Ohms lov gjelder for mange kretsløp. Kilde: Wikimedia Commons. Tlapicka [CC BY-SA 3.0 (https: // creativecommons.Org/lisenser/by-SA/3.0)]

Hvor Z Det er impedansen, som også representerer motstanden mot passering av vekselstrømmen med et kretselement, for eksempel en kondensator eller en induktans.

Det skal bemerkes at ikke alle kretsmaterialer og elementer overholder Ohms lov. Til de der det er gyldig, kalles elementer Ohmic, Og der det ikke er oppfylt, kalles de Ingen-ohmisk eller ikke -lineær.

Vanlige elektriske motstander er ohmiske, men dioder og transistorer er ikke, siden forholdet mellom spenning og strøm ikke er lineær i dem.

Ohms lov skylder navnet sitt til den tyske fysikeren og matematisk. Til hans ære er enheten for elektrisk motstand i det internasjonale systemet utnevnt: Ohm, som også kommer til uttrykk av det greske bokstaven ω.

[TOC]

Hvordan beregnes det?

Selv om den makroskopiske formen for Ohms lov er den mest kjente, siden den kobler beløp som er lett målbare i laboratoriet, er det Mikroskopisk form relaterer to viktige vektormengder: det elektriske feltet OG og strømtetthet J:

J = σ.OG

Der σ er materialets elektriske ledningsevne, en egenskap som indikerer lettheten den må drive strøm. For sin del J Det er en vektor hvis størrelse er kvotienten mellom den nåværende intensiteten I og området av tverrsnittet som den sirkulerer.

Det kan tjene deg: Overfladiske bølger: Karakteristikker, typer og eksempler

Det er logisk å anta at det er en naturlig sammenheng mellom det elektriske feltet inne i et materiale og den elektriske strømmen som sirkulerer gjennom det, for eksempel de største vanligere.

Men strømmen er ikke en vektor, siden den ikke har en adresse i verdensrommet. I stedet vektoren J Det er vinkelrett - eller normalt - til korsets seksjonsområde for sjåføren, og dets betydning er det for strømmen.

Fra denne formen for Ohms lov er den første ligningen nådd, forutsatt at en lengde driver og tverrsnitt A, og erstatter størrelsen på J og OG av:

J = i/a

E = v/ℓ

J = σ.E → i/a = σ. (V/ℓ)

V = (ℓ/σ.TIL).Yo

Det inverse av konduktivitet kalles Motstand Og det er betegnet med det greske bokstaven ρ:

1/ σ = ρ

Derfor:

V = (ρℓ/ a).I = r.Yo

Motstanden til en sjåfør

I ligningen V = (ρℓ/ a).Yo, Konstanten (ρℓ/ a) Det er derfor motstand:

R = ρℓ/ a

Drivermotstand avhenger av tre faktorer:

-Hans resistivitet ρ, typisk for materialet han er produsert.

-Lengden ℓ.

-Område A i tverrsnittet.

En større ℓ, større motstand, ettersom nåværende bærere har flere muligheter til å kollidere med de andre partiklene inne i føreren og miste energi. Og tvert imot, for større a, er det lettere for nåværende transportører å bevege seg på en ryddig måte av materialet.

Til slutt, i molekylstrukturen til hvert materiale, ligger det enkle som et stoff lar den elektriske strømmen passere. For eksempel er metaller som kobber, gull, sølv og platina, med lav resistivitet, gode ledere, mens tre, gummi og olje ikke er, så de har større resistivitet.

Eksempler

Her er to illustrerende eksempler på Ohms lov.

Eksperimenter for å sjekke Ohms lov

En enkel opplevelse illustrerer Ohms lov, for dette er et stykke ledende materiale, en variabel spenningskilde og et multimeter nødvendig.

Kan tjene deg: trykkmålere

Blant endene av det ledende materialet er det etablert en spenning V som bør variere gradvis. Med den variable strømkilden kan verdiene på nevnte spenning fikses, som måles med multimeteret, så vel som strømmen I sirkulerer av driveren.

Parene av verdier V og jeg er registrert i en tabell og med dem er en graf på millimeterpapir bygget. Hvis den resulterende kurven er en linje, er materialet ohmisk, men hvis det er noen annen kurve, er materialet ikke -ohmisk.

I det første tilfellet kan linjens skråning bestemmes, noe som tilsvarer førerens motstand eller den omvendte, konduktansen.

I det følgende bildet representerer den blå linjen en av disse grafikken for et ohmisk materiale. I mellomtiden er gule og røde kurver av ikke-oshmiske materialer, for eksempel en halvleder, for eksempel.

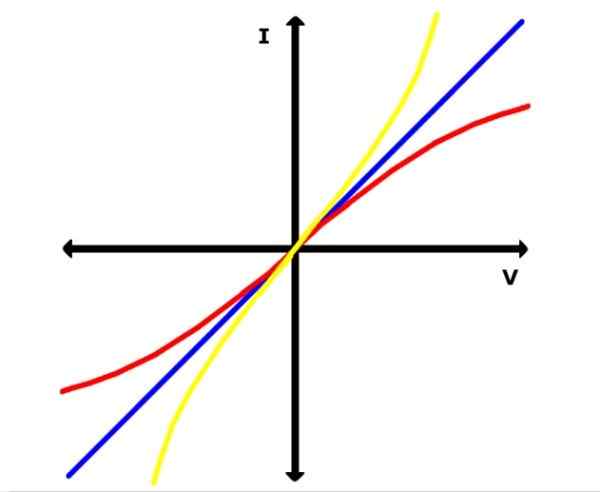Figur 2. Graf I Vs. V for ohmiske materialer (blå rett) og ikke-osohmiske materialer. Kilde: Wikimedia Commons.

Hydraulisk analogi av Ohms lov

Det er interessant å vite at den elektriske strømmen i Ohm -loven har en lignende oppførsel på en viss måte som vann som sirkulerer gjennom et rør. Den engelske fysikeren Oliver Lodge var den første som foreslo simulering av nåværende oppførsel gjennom hydrauliske elementer.

For eksempel representerer rørene lederne, siden vannet sirkulerer gjennom dem og de nåværende transportørene gjennom det siste. Når det er en innsnevring i røret, er vannpassasjen vanskelig, så dette vil være ekvivalent med elektrisk motstand.

Trykkforskjellen i to ender av røret lar vann strømme, noe som gir en forskjell i høyder eller en vannpumpe, og analogt er potensialforskjellen (batteriet) den som holder den bevegelige belastningen, tilsvarer strømning eller volum på Vann per tidsenhet.

Det kan tjene deg: konveksjon varmeoverføring (med eksempler)

En stempelpumpe ville representere rollen som en alternativ spenningskilde, men fordelen med å sette en vannpumpe er at den hydrauliske kretsen ville være lukket, da en elektrisk krets skal være å strømme strøm.

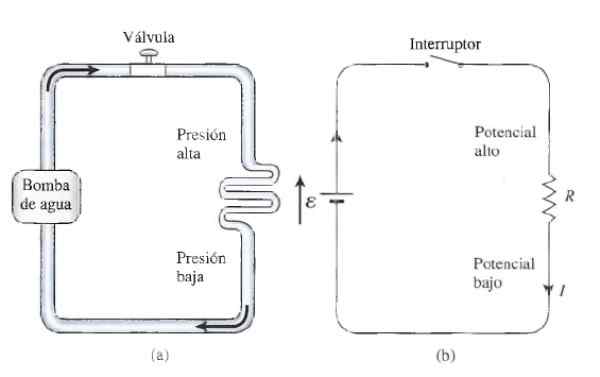Figur 3. Hydraulisk analogi for OHM -lov: I A) et vannstrømsystem og i B) en enkel resistiv krets. Kilde: Tippens, P. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.

Motstand og brytere

Tilsvarer en bryter i en krets ville være en passeringsnøkkel. Det tolkes på denne måten: Hvis kretsen er åpen (lukket passasje), kan strømmen, så vel som vannet, ikke strømme.

På den annen side, med den lukkede bryteren (helt åpen trinntast) kan både strømmen og vannet sirkulere uten problemer av føreren eller røret.

Passasjetasten eller ventilen kan også representere en motstand: når nøkkelen åpnes fullstendig, tilsvarer det å ha en nullmotstand eller kortslutning. Hvis det i det hele tatt lukkes, er det som å ha den åpne kretsen, mens delvis lukket er det som å ha en motstand på en viss verdi (se figur 3).

Øvelser

- Oppgave 1

Det er kjent at en elektrisk plate krever 2 A ved 120 V for å fungere ordentlig. Hva er din motstand?

Løsning

Motstanden blir ryddet fra Ohms lov:

R = V/ I = 120 V/ 2 A = 60 Ω

- Oppgave 2

En ledning på 3 mm og 150 m lang har 3 3.00 Ω ved 20 ° C. Finn motstanden til materialet.

Løsning

Ligningen R = ρℓ/ a er passende, Derfor er det nødvendig å finne først i området for tverrsnittet:

A = π(D/2)² = π (3 x 10^-3 m/2)² = 4.5π x 10 ^-6 m²

Endelig når du erstatter får du:

ρ = a.R /ℓ = 4.5π x 10 ^-6 m² x 3 Ω / 150 m = 2.83 x 10 ^-7 Ω.m

Referanser

1. Resnick, r. 1992.Fysisk. Tredje utgave utvidet på spansk. Volum 2. Continental Editorial Company s.TIL. Av c.V.
2. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14^th. Ed. Volum 2. 817-820.
3. Serway, r., Jewett, J. 2009. Fysikk for vitenskap og ingeniørfag med moderne fysikk. 7. utgave. Volum 2. Cengage Learning. 752-775.
4. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.
5. Sevilla University. Department of Applied Physics III. Tetthet og strømintensitet. Gjenopprettet fra: oss.er.
6. Walker, J. 2008. Fysikk. 4. utg. Pearson.725-728