Kongruens kongruente figurer, kriterier, eksempler, øvelser

De sammenfallende, I geometri påpeker han at hvis to flate figurer har samme form og dimensjoner, er disse kongruente. For eksempel er to segmenter kongruente når lengden er like. Også de kongruente vinklene har samme tiltak, selv om de ikke er orientert på samme måte i flyet.

Begrepet "kongruens" kommer fra latin Kongruentia, hvis betydning er korrespondanse. Dermed tilsvarer to kongruente figurer nøyaktig det ene med den andre.

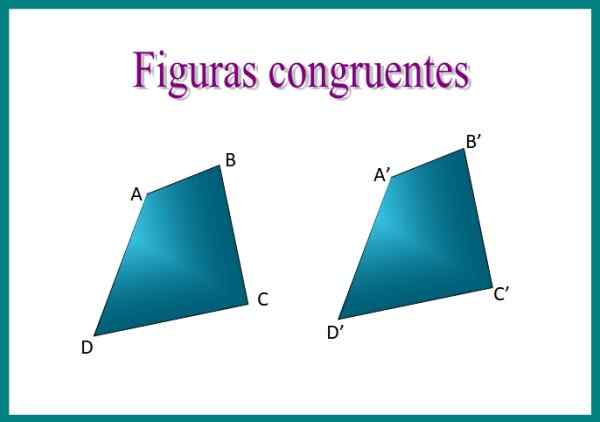
Figur 1. Kvadrilateralsene ABCD og A'B'C'd 'av figuren er kongruente: sidene deres har samme mål, så vel som deres indre vinkler. Kilde: f. Zapata.

For eksempel, hvis vi overlapper de to firedoblingene av bildet, vil vi oppdage at de er kongruente, siden disposisjonen til sidene er identiske og de måler det samme.

Når du plasserer kvadrilateralsene ABCD og A'b'c'd 'den ene på den andre, vil figurene sammenfalle nøyaktig. De matchende sidene kalles homologe sider enten tilsvarende Og for å uttrykke kongruens er symbolet ≡ brukt. Da kan vi si at abcd ≡ a'b'c'd '.

[TOC]

Kongruenskriterier

Følgende egenskaper er vanlige for kongruente polygoner:

-Like form og størrelse.

-Identiske mål på vinklene dine.

-Samme grad på hver av sidene.

I tilfelle to polygoner det gjelder er regelmessige, det vil si at alle sider og indre vinkler måler det samme, er kongruensen sikret når en av følgende forhold er oppfylt:

-Sidene er kongruente

-De Apothems har samme mål

-Han radio av hver polygon måler det samme

Apotemen til en vanlig polygon er avstanden mellom sentrum og en av sidene, mens radius tilsvarer avstanden mellom sentrum og et toppunkt eller hjørne av figuren.

Kongruenskriterier brukes ofte fordi mange deler og stykker av alle slag er produsert i serie og må ha samme form og tiltak. På denne måten kan de enkelt byttes ut når det er nødvendig, for eksempel nøtter, skruer, ark eller brosteinsbelagte bakken i gaten.

Kan tjene deg: Simpson Rule: Formel, demonstrasjon, eksempler, øvelserFigur 2. Gatekoblinger er kongruente figurer, siden deres form og dimensjoner er nøyaktig de samme, selv om orienteringen deres på gulvet kan endre seg. Kilde: Pixabay.

Kongruens, identitet og likhet

Det er for eksempel geometriske begreper relatert til kongruens De identiske figurene og Lignende figurer, som ikke nødvendigvis innebærer at tallene er kongruente.

Legg merke til at de kongruente figurene er identiske, men kvadrilateralsene i figur 1 kan være orientert på forskjellige måter på planet og fortsatt fortsette å være kongruent, siden den forskjellige orienteringen ikke endrer størrelsen på sidene eller den i vinklene deres. I dette tilfellet ville de slutte å være identiske.

Det andre konseptet er det av likheten mellom figurer: to flate figurer er like hvis de har samme form og deres indre vinkler måler det samme, selv om størrelsen på figurene kan være forskjellige. Hvis dette er tilfelle, er ikke tallene kongruente.

Kongruenseksempler

- Kongruens av vinkler

Som vi antydet i begynnelsen, har de kongruente vinklene samme tiltak. Det er flere måter å oppnå kongruente vinkler på:

Eksempel 1

To linjer med et felles punkt definerer to vinkler, kalt Motsatte vinkler av toppunktet. Disse vinklene har samme tiltak, derfor er de kongruente.

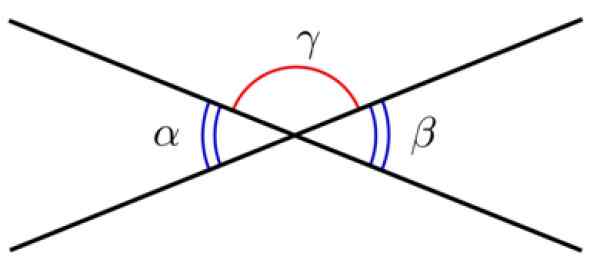Figur 3. Motsatte vinkler av toppunktet. Kilde: Wikimedia Commons.

Eksempel 2

Det er to parallelle linjer pluss en linje t som krysser dem begge. Som i forrige eksempel, når denne linjen krysser parallellene, genererer den kongruente vinkler, en på hver linje til høyre side og to andre på venstre side. Figuren viser α og α₁, til høyre for linjen t, De er kongruente.

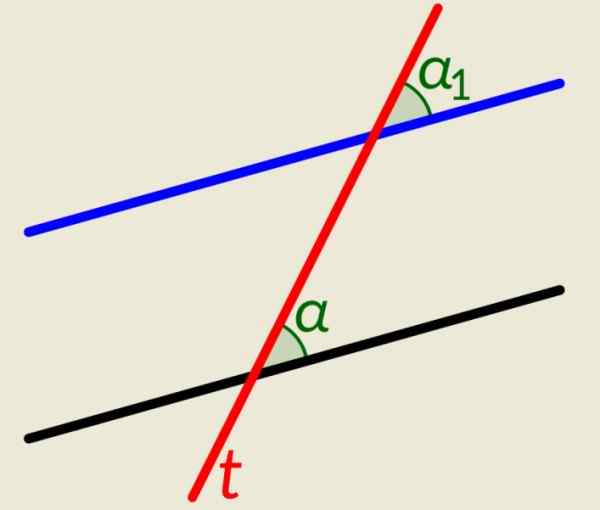Figur 4. Vinklene vist på figuren er kongruente. Kilde: Wikimedia Commons. Lfahlberg/CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0).

Eksempel 3

I et parallellogram er det fire interne vinkler, som er kongruente to til to. De er de mellom motsatte hjørner, som vist i følgende figur, der de to grønne vinklene er kongruente, så vel som de to vinklene i rødt.

Kan tjene deg: Acutangle Triangle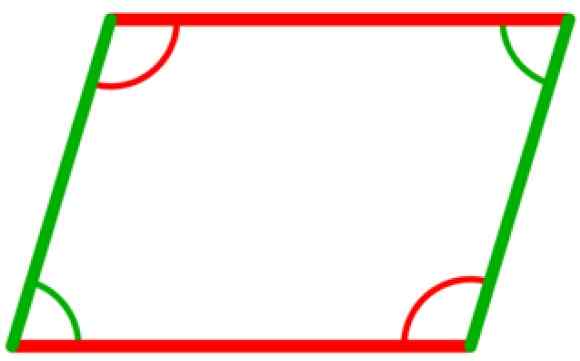Figur 5. De interne vinklene til parallellogrammet er kongruente to til to. Kilde: Wikimedia Commons.

- Kongruens av trekanter

To trekanter med identisk form og samme størrelse er kongruente. For å bekrefte dette er det tre kriterier som kan undersøkes på jakt etter kongruens:

-LLL -kriterier: De tre sidene av trekantene har de samme tiltakene, derfor l₁ = L '₁; L₂ = L '₂ og jeg₃ = L '_3.

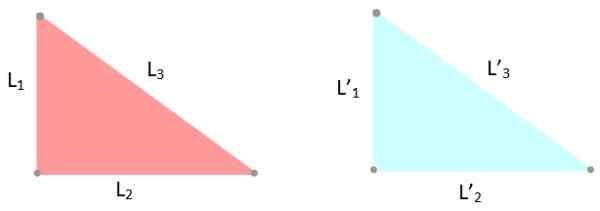Figur 6. Eksempel på kongruente trekanter, hvis sider måler det samme. Kilde: f. Zapata.

-Kriterier Alla y aal: Trekantene har to like interne vinkler og siden mellom disse vinklene har samme mål.

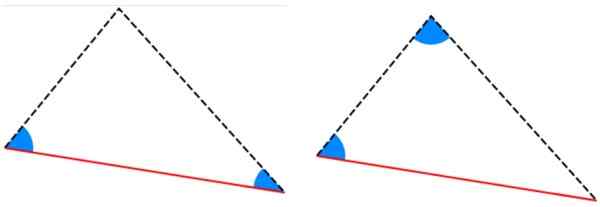Figur 7. Kriterier Ala og Aal for kongruens av trekanter. Kilde: Wikimedia Commons.

-LAL -kriterier: To av sidene er identiske (tilsvarende), og blant dem er det samme vinkel.

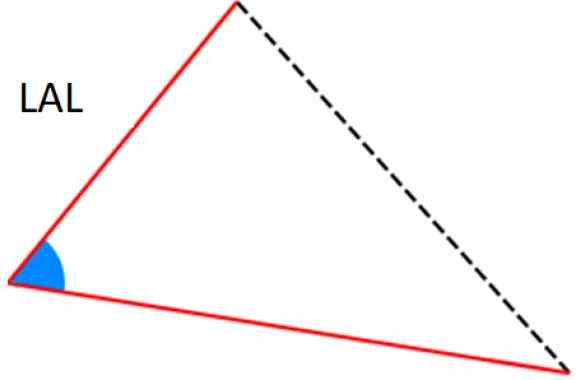Figur 8. LAL -kriterier for kongruens av trekanter. Kilde: Wikimedia Commons.

Løste øvelser

- Oppgave 1

I følgende figur er to trekanter vist: ΔABC og ΔECF. Det er kjent at AC = EF, at AB = 6 og at CF = 10. I tillegg er vinklene ∡bac og ∡fec kongruente og vinklene ∡ACB og ∡fcb er også.

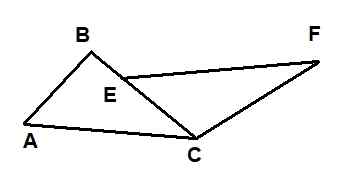Figur 9. Trekanter for eksemplet løst 1. Kilde: f. Zapata.

Da er lengden på BE -segmentet lik:

(i) 5 

(Ii) 3

(Iii) 4 

(Iv) 2

(v) 6

Løsning

Ettersom de to trekantene har en side av lik lengde ac = ef mellom like vinklene ∡bac = ∡cef og ∡bca = ∡cfe, kan det sies at de to trekantene er kongruente av kriteriene vingen.

Det er Δbac ≡ ΔCEF, så du må:

Ba = ce = ab = 6

BC = CF = 10

Ac = ef

Men segmentet du vil beregne er = BC - EC = 10 - 6 = 4.

Slik at riktig svar er (III).

- Oppgave 2

Tre trekanter vises på figuren. Det er også kjent at de to indikerte vinkler måler 80º hver og at segmentene AB = PD og AP = CD. Finn verdien av vinkel x angitt i figuren.

Det kan tjene deg: polybal grafikk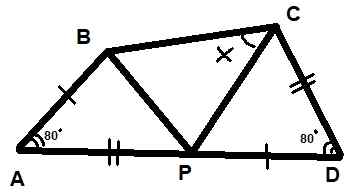Figur 10. Trekanter for eksemplet løst 2. Kilde: f. Zapata.

Løsning

Du må bruke egenskapene til trekantene, som er detaljert trinn for trinn.

Trinn 1

Fra og med kriteriene for kongruens av Lal -trekanter, kan det sies at BAP- og PDC -trekantene er kongruente:

Δbap ≡ ΔPDC

Steg 2

Ovennevnte fører til å bekrefte at BP = PC, derfor er trekanten Δbpc isosceles og ∡pcb = ∡pbc = x.

Trinn 3

Hvis vi ringer γ i BPC -vinkelen, følger det at:

2x + γ = 180º

Trinn 4

Og hvis vi ringer β til APB- og DCP- og α -vinklene til ABP- og DPC -vinklene, må det:

α + β + γ = 180º (siden APB er en flat vinkel).

Trinn 5

I tillegg α + β + 80º = 180º etter sum av interne vinkler av APB -trekanten.

Trinn 6

Kombinere alle disse uttrykkene du må:

α + β = 100º

Trinn 7

Og derfor:

γ = 80º.

Trinn 8

Endelig følger det det:

2x + 80º = 180º

Med x = 50º.

Referanser

1. Baldor, a. 1973.Flat og romgeometri. Sentralamerikansk kulturell.
2. CK-12 Foundation. Kongruente polygoner. Hentet fra: CK 12.org.
3. Kos deg med matematikk. Definisjoner: radio (polygon). Gjenopprettet fra: Nytmatimaticas.com.
4. Matematikk åpen referanse. Testing av polygoner for kongruens. Gjenopprettet fra: Mathpenref.com.
5. Wikipedia. Kongruens (geometri). Gjenopprettet fra: er.Wikipedia.org.
6. Zapata, f. Trekanter, historie, elementer, klassifisering, egenskaper. Hentet fra: Lifer.com.