Proporsjonalitet konstant hva er, beregning, øvelser

De proporsjonalitetskonstant Det er et relasjonelt numerisk element, som brukes til å definere likhetsmønsteret mellom 2 størrelser som samtidig endres. Det er veldig vanlig å representere det som en generisk lineær funksjon gjennom uttrykk f (x) = k.X. Dette er imidlertid ikke den eneste representasjonen av en mulig proporsjonalitet.

For eksempel har forholdet mellom x og y i y = 3x -funksjonen en konstant av proporsjonalitet lik 3. Det viser at når den uavhengige variabelen X vokser, gjør det også den avhengige variabelen og i trippel av sin forrige verdi.

Endringene som brukes i den ene variabelen, har umiddelbare konsekvenser på den andre, slik at det er en verdi kjent som konstant proporsjonalitet. Dette tjener til å relatere de forskjellige størrelsene som begge variablene skaffer seg.

[TOC]

Hva er konstanten av proporsjonalitet og typer

I henhold til trenden med å endre variablene, kan proporsjoner klassifiseres i to typer.

Direkte proporsjonalitet

Antyder et ensrettet forhold mellom to størrelser. I den, hvis den uavhengige variabelen presenterer en viss vekst, vil den avhengige variabelen også vokse. Tilsvarende vil enhver reduksjon i den uavhengige variabelen føre til en nedgang i størrelsen på og.

For eksempel den lineære funksjonen som ble brukt i introduksjonen; Y = 3x, tilsvarer et direkte forhold mellom proporsjonalitet. Dette er fordi økningen i uavhengig variabel x vil føre til en økning i trippel i den forrige verdien tatt av den avhengige variabelen og.

Tilsvarende vil den avhengige variabelen redusere tredoblingen av verdien når x stiger ned i størrelsesorden.

Verdien av proporsjonalitetskonstanten "k" i et direkte forhold er definert som k = y/x.

Omvendt eller indirekte proporsjonalitet

I denne typen funksjoner presenteres forholdet mellom variablene på en antonym måte, der veksten eller reduksjonen av den uavhengige variabelen tilsvarer henholdsvis reduksjon eller vekst av den avhengige variabelen.

Det kan tjene deg: nedbrytning av naturlige tall (eksempler og øvelser)

For eksempel er funksjonen f (x) = k/x et omvendt eller indirekte forhold. Siden verdien av den uavhengige variabelen begynner å øke, vil verdien av k deles med et voksende tall, noe som gjør den avhengige variabelen reduksjon i verdi i henhold til andelen.

I henhold til verdien som er tatt av K, kan tendensen til den proporsjonale inverse funksjonen defineres. Hvis k> 0, vil funksjonen avta i alle reelle tall. Og grafen vil være lokalisert i 1. og 3. kvadrant.

Tvert imot, hvis verdien av k er negativ eller mindre enn null, vil funksjonen øke og grafen vil bli funnet i 2. og 4 kvadrant.

Hvordan beregnes det?

Det er forskjellige sammenhenger der definisjonen av proporsjonalitetskonstanten kan være nødvendig. I forskjellige tilfeller vil forskjellige data om problemet vises, der studiet av disse endelig vil vise verdien av k.

På en generisk måte kan de nevnte rekapituleres rekapituleres. Verdiene til k tilsvarer to uttrykk i henhold til typen proporsjonalitet som er til stede:

- Direkte: k = y/x

- Omvendt eller indirekte: k = y.X

I henhold til grafen din

Noen ganger vil bare grafen til en funksjon være kjent delvis eller fullstendig. I disse tilfellene vil det være nødvendig, ved grafisk analyse, bestemme type proporsjonalitet. Da må vi definere en koordinat som gjør det mulig å bekrefte verdiene til X og Y for å gjelde den tilsvarende K -formelen.

Grafene som refererer til direkte proporsjoner er av lineær type. På den annen side tar grafene med inverse proporsjonale funksjoner vanligvis form av hyperbolas.

I henhold til tabell over verdier

I noen tilfeller er det en tabell med verdier med verdiene som tilsvarer hver iterasjon av den uavhengige variabelen. Normalt innebærer dette realiseringen av grafen i tillegg til å definere verdien av k.

Kan tjene deg: Frekvensfordeling: Hvordan lage et bord, eksempel, trening

I følge analytisk uttrykk

Viser uttrykket som definerer analytisk. Direkte kan verdien av k være klar, eller det kan også utledes fra selve uttrykket.

Som regel på tre direkte eller sammensatte

I andre treningsmodeller er det visse data, som refererer til forholdet mellom verdier. Dette gjør nødvendig anvendelse av tre direkte eller sammensatte for å definere andre nødvendige data i året.

Historie

Konseptet med proporsjonalitet har alltid vært til stede. Ikke bare i sinnet og arbeidet til de store matematikerne, men i befolkningenes daglige liv, på grunn av deres praktiske og anvendbarhet.

Det er veldig vanlig å oppfylle situasjoner som krever en proporsjonalitetstilnærming. Disse presenteres i hvert tilfelle der variabler og fenomener blir sammenlignet som holder visse forhold.

Gjennom en tidslinje kan vi karakterisere historiske øyeblikk, der matematiske fremskritt angående proporsjonalitet er blitt brukt.

- Andre århundre a.c. Brøkdelen og proporsjonene lagringssystem i Hellas blir vedtatt.

- 5. århundre a.c. Andelen som relaterer siden og diagonalen til en firkant blir også oppdaget i Hellas.

- 600 a.c. Tales de Mileto presenterer sitt teorem om proporsjonalitet.

- År 900. Desimalsystemet som tidligere er brukt av India av grunner og proporsjoner er utvidet. Bidrag gitt av araberne.

- Xvii århundre. Bidrag refererer til proporsjonene i beregningen av Euler ankommer.

- XIX Century. Gauss gir konseptet med komplekst antall og proporsjoner.

- Tjuende århundre. Proporsjonalitet som funksjonsmodell er definert av sukker og deulofeo.

Løste øvelser

Oppgave 1

Det er påkrevd å beregne verdien av variablene x, y, z og g. Å vite følgende proporsjonale forhold:

3x + 2y - 6z + 8g = 1925

Kan tjene deg: kontinuerlig tilfeldig variabel

x/3 = y/8 = z/3 = g/5

De relative verdiene for proporsjonalitetskonstanten er definert. Disse kan fås fra det andre forholdet, der verdien som deler hver variabel indikerer et forhold eller grunn angående k.

X = 3K y = 2K z = 3K g = 5k

Verdiene erstattes i det første uttrykket, der det nye systemet vil bli evaluert i en enkelt K -variabel.

3 (3K) + 2 (2K) - 6 (3K) + 8 (5K) = 1925

9k + 4k -18k + 40k = 1925

35k = 1925

K = 1925/35 = 55

Ved å bruke denne verdien av proporsjonalitetskonstanten kan vi finne figuren som definerer hver av variablene.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Oppgave 2

Beregn proporsjonalitetskonstanten og uttrykket som definerer funksjonen, gitt grafikken.

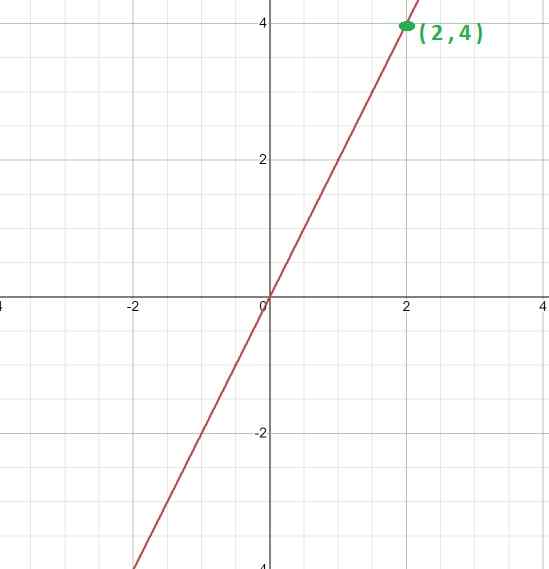
For det første blir grafen analysert, den lineære karakteren er tydelig. Dette indikerer at det er en funksjon med direkte proporsjonalitet og at verdien av k vil oppnås gjennom uttrykket k = y/x

Deretter velges et bestemmbart punkt på grafen, det vil si hvor koordinatene som utgjør det kan være nøyaktig.

For dette tilfellet er poenget tatt (2, 4). Hvor kan vi etablere følgende forhold.

K = 4/2 = 2

Slik at uttrykket er definert av y = kx -funksjonen, som for dette tilfellet vil være

F (x) = 2x

Referanser

1. Matematikk for elektrisitet og elektronikk. Dr. Arthur Kramer. Cengage Learning, 27. juli. 2012
2. Visjon 2020: Den strategiske rollen til operativ forskning. N. Ravichandran. Allied Publisher, 11. september. 2005
3. Grammatisk og aritmetisk kunnskap om statlig administrativ assistent.e-bok. Mad-Eduform
4. Matematikkforsterkning for læreplanstøtte og diversifisering: for læreplanstøtte og diversifisering. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29. august. 2003
5. Logistikk og kommersiell styring. Maria José Escudero Serrano. Paraninfo Editions, S.TIL., 1. september. 2013