Kriterier lignende trekanter

Hva er trekantene likhetskriterier?

Triangles -likhetskriteriene er reglene som tillater å vite om to trekanter er like. Likheten mellom geometriske figurer, inkludert trekanter, krever at tallene har på samme måte, selv om de ikke nødvendigvis har samme størrelse eller samme retning.

For at to trekanter skal være like, er det nødvendig at: i) deres homologe sider er proporsjonale og ii) de indre vinklene til hver har samme mål.

Figur 1. To lignende trekanter: Selv om de ikke har samme størrelse, er sidene proporsjonale og deres indre vinkler har like store mål. Kilde: f. Zapata.

Et proporsjonalt forhold eller andel mellom to mengder A og B er representert med A/B -forholdet, med B ≠ 0. For lignende trekanter er følgende proporsjoner mellom sidene gyldige:

a/a '= b/b' = c/c '= r

Verdien av r kalles Likhetsgrunner.

I tillegg må de tilsvarende interne vinklene være av samme tiltak, derfor: ∠A = ∠A '; ∠B = ∠B 'og ∠C = ∠C'. I henhold til disse forholdene er trekantene likhetskriterier:

Kriterier 1: To trekanter er like hvis de har to indre vinkler med like mål. I så fall måler den tredje vinkelen også den samme, siden summen av de indre vinklene i en hvilken som helst trekant er 180º:

α = α '; β = β '

Kriterier 2: Trekantene er like hvis to homologe sider er proporsjonale og vinkelen mellom dem er den samme:

a/a '= b/b'; α = α '

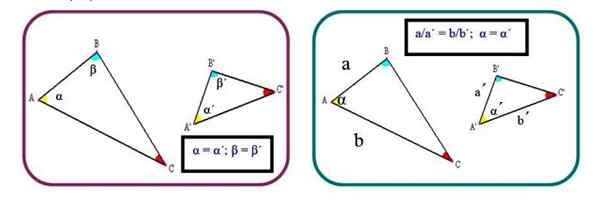Figur 2. To kriterier for å etablere likheten mellom trekanter. Kilde: f. Zapata.

Kriterier 3: De tre homologe sidene er proporsjonale:

a/a '= b/b' = c/c '= r

Eksempler

Likheten mellom trekanter er veldig nyttig for beregning av høyder og avstander som ikke er lett målbare direkte. Gjennom noen enkle beregninger er det mulig å finne ut disse lengdene ved å sammenligne lignende trekanter.

Kan tjene deg: grunnleggende teorem om aritmetikk: demonstrasjon, applikasjoner, øvelser

Høyden på søyler, bygninger og trær

Det sies at faren til geometri i det gamle Hellas, som Miletus (625-547 til.C.), beregnet høyden på søylen til et tempel uten behov for spesielle instrumenter, bare sammenligne lengden på skyggen på stokken med den for kolonnen og bruke likheten til trekanter. Med den samme metoden klarte han å måle høyden på den store pyramiden i Egypt og dermed imponere farao.

Avstanden til månen

Det er et enkelt eksperiment som gjøres for å beregne avstanden mellom jorden og månen. Det krever en valuta, litt limtape og en vernier eller en kandidatregel. Når månen er full, er valutaen festet til glasset i et vindu og månen blir observert med det ene øyet, plassert på en slik måte at valutaen dekker bare fullmånen.

Når dette skjer, er årsaken mellom diameteren på valutaen og avstanden mellom øyet og valutaen den samme som det er mellom månens diameter og avstanden mellom øyet og månen:

Valutameter/avstand Valuta = Månediameter/avstand til månen

Årsaken er omtrent 1/110. Noe som betyr at avstanden til månen er 110 ganger diameteren på dette.

For øyeblikket er månens radius estimert i 1737.1 km, så diameteren er 3474.2 km. Ved å erstatte denne verdien i forholdet:

Avstand til månen = månediameter ÷ (valutadiameter/avstand til valutaen)

Er oppnådd:

Avstand til månen = 3474.2 km ÷ (1/110) = 382.162 km

Det kan tjene deg: hepagonal prisme

Veldig nær verdien som er etablert av 384 astronomer.000 km.

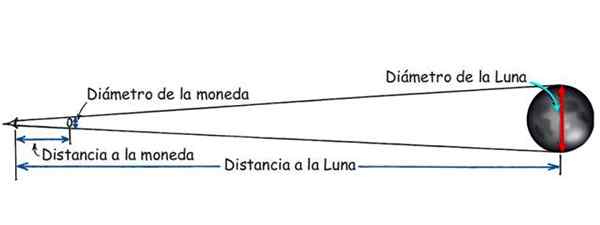Figur 3. Avstanden til månen kan være kjent takket være likheten i trekantene. Kilde: Modified Hewitt, P. Konseptuell fysikk.

Avstand mellom et skip og kysten

For å måle avstanden mellom skipet og kysten, sitter innsatser på stranden i punkt A, B, C og Q. ABC- og PCQ -trekanter er like med kriterier 1, siden de har to like vinkler: de to vinklene ∠C = α som er motarbeidet av toppunktet og de to rette vinklene lik 90º: ∠B = ∠Q.

To trekanter som ligger på denne måten sies å være i Thales -stilling Og de er alltid like. Trekanter er identifisert i Thales -posisjonen for å ha en felles vinkel, og motsatte sider i den vinkelen er parallell.

I neste avsnitt er det en øvelse med numeriske verdier.

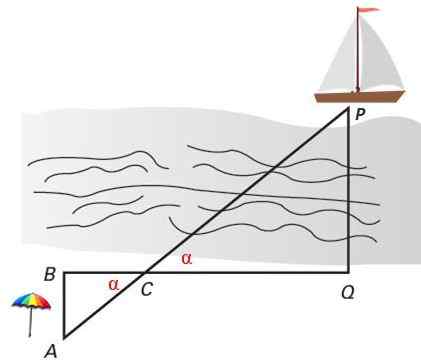Figur 4. To lignende trekanter i Thales -stilling tjener til å beregne den vinkelrett avstanden til et skip til kysten. Kilde: f. Zapata.

Løste øvelser

Oppgave 1

Du vil finne ut hvor langt seilbåten er forankret i forrige figur, fra et punkt som ligger ved bredden av stranden, som innsatser er spikret i punkt A, B, C og Q, og dermed bestemme trekanten ABC, som ligner på PCQ, men hvis sider er lettere å måle.

Beregn den vinkelrette avstanden PQ mellom skipet og kysten, med likheten mellom trekanter, hvis avstandene som er tilgjengelige er:

Ab = 12 m

BC = 16 m

QC = 60 m

Løsning

Andelene mellom homologe sider er:

Ab/qp = bc/cq = 16 m/60 m = 0.267

Derfor 0.267 er årsaken til likhet:

Ab/qp = 0.267

QP = AB / 0.267 = 12 m / 0.267 = 44.9 m

Oppgave 2

I følgende trekant: Hvor mye måler annonsesegmentet?

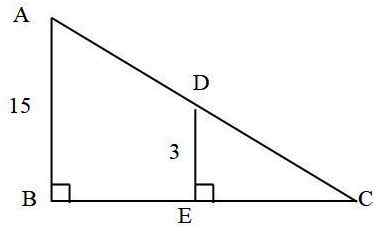
Det er kjent at:

• AC = 25 cm
• Ab = 15 cm
• De = 3 cm

Kan tjene deg: Multipler av 2: Hva er og forklaring

Løsning

Trekantene er like, fordi de deler en vinkel som er ∠C og sidene av og AB er parallelle. Likhetsforholdet beregnes av:

R = ab / de = 15 cm / 3 cm = 5

Og også gjennom:

R = AC / DC

Derfor DC = AC / R = 25 cm / 5 = 5 cm

Siden:

AC = AD + DC

Det følger at AD = AC - DC = 25 cm - 5 cm = 20 cm

Øvelse 3

En isosceles -trekant har en omkrets på 49 cm og en base på 21 cm. Beregn omkretsen til en trekant som ligner på denne, men hvis base måler 4 cm.

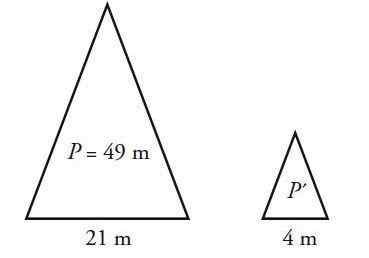
Løsning

Isosceles -trekanten har to like sider, forskjellig fra base b. La ℓ Målet på sidene og p omkretsen, som består av summen av de tre sidene. For den største trekanten:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Nå er andelen mellom sidene av trekantene hevet, de av den lille trekanten er symbolisert med premier:

B/ b '= ℓ/ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

Omkretsen til den lille trekanten vil være:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. 5. plass. Ed. Pearson.
3. Clemens, s. Geometri med applikasjoner. Addison Wesley.
4. Ibáñez, p. 2010. Matematikk III. Cengage Learning.
5. Jiménez, r. Matematikk II: Geometri og trigonometri. 2. Utgave. Pearson.
6. Stewart, J. 2007. Forkalkning. 5. plass. Utgave. Cengage Learning.
7. Vicmat. Samos Aristarco: Solsystemtiltak. Gjenopprettet fra: vicmat.com