Stiv kropp
- 2208
- 272
- Oliver Christiansen
Hva er en stiv kropp?
En stiv kropp er et materielt objekt hvis partikler alltid forblir i de samme relative posisjonene. Derfor er det et objekt som ikke er deformert, en kvalitet tilskrevet de intense samholdskreftene som holder partiklene på plass.
Faktisk har partiklene til ethvert legeme som er utsatt for ytre krefter en tendens til å vibrere eller bevege seg, så objektet er alltid deformert til en viss grad, men disse effektene er vanligvis små.
Når dette er tilfelle, kan det antas at kroppen er stiv og har en veldig god tilnærming til atferden, selv om det er en idealisering.
Stive kroppstyper
Du kan skille to typer stiv kropp:
- De hvis partikler kommer i diskrete mengder, det vil si at de kan telle. For eksempel kan to metallfærer koblet med en tynn og lett stang betraktes som en unik enhet. Hvis stangen er stiv nok til ikke å bøye seg, regnes systemet som en stiv kropp.
- De som er kontinuerlige, noe som betyr at partiklene som utgjør dem kan ikke skilles. Hverdags- og naturobjekter er gode eksempler: steiner, møbler og andre, så vel som landet og andre himmelske bergarter steinete.
Stiv kroppsbevegelse og dynamikk
Som objekter som betraktes som partikler, kan stive kropper overføres, rotere og ha en mer generell bevegelse, og kombinerer oversettelse og rotasjon.
For å studere oversettelsen er det ikke nødvendig.
Disse oversettelses- og rotasjonsbevegelsene kan være:
- Uavhengig, som i tilfelle av planetene, som har en rotasjonsbevegelse rundt deres akse (ansett som faste) og en annen av oversettelsen rundt solen, men hastighetene til hver enkelt er ikke relatert.
- Ødelagt trash, hvis vinkelhastigheten og oversettelseshastigheten til massesenteret er relatert. I dette tilfellet er rotasjonsaksen mobil, som for sylinderen som går ned skyting uten å gli i en skrå skråning.
Dynamikken i stivt faststoff
Følgende størrelser er relevante i dynamikken i stivt faststoff:
Massesenter
Massesenteret er punktet der hele kroppen i kroppen anses å være konsentrert. Hvis det er en homogen og symmetrisk kropp, som en sfære, sammenfaller massesenteret med det geometriske sentrum.
Treghetens øyeblikk
Denne skalære størrelsen er verdien av rotasjons treghet eller motstand som motsetter seg et objekt for å rotere rundt en viss akse. Det avhenger helt av geometrien til objektet og dens masse, og i visse tilfeller er det lettere å snu visse akser enn på andre.
For kropper med godt definerte geometriske former, er det tabeller med treghetsmomenter med hensyn til symmetriaksene, for eksempel den som passerer gjennom massesenteret. Med denne informasjonen og teoremene relatert til treghetens øyeblikk, kan øyeblikkene med hensyn til andre akser enkelt beregnes.
Krefter og dreiemoment eller dreiemoment
Krefter er pålagt å flytte et legeme. Hvis det stive solide massesenteret beveger seg, er bevegelsesligningen, i henhold til Newtons andre lov,:
FNett = M ∙tilCM
Hvor:
-Nettstyrken er FNett
-M er massen
-Akselerasjonen av massesenteret er tilCM
Imidlertid gjør ikke alle anvendte krefter objektet til å bryte. For å gjøre dette er det nødvendig. Det er definert som vektorproduktet mellom posisjonsvektoren r Angående et bestemt punkt og kraft F i spørsmålet. Det er betegnet med det greske brevet τ (I fet bokstav er det også en vektor):
Kan tjene deg: elliptisk bevegelseτ = r × F
I det internasjonale systemet er dreiemomentheten N⋅m (Newton per meter).
I mange tilfeller beskrives rotasjonsbevegelsen rundt en akse som passerer gjennom massesenteret av en analog ligning til Newtons andre lov:

Kinetisk energi av et stivt fast stoff
Bevegelsen av et stivt legeme er beskrevet av oversettelser av sentrum av masse og rotasjoner rundt det punktet, derfor har den kinetiske energien begge bidrag.
La K den kinetiske energien i kroppen, vCM Hastigheten på massesenteret, m massen av kroppen, ogCM treghetens øyeblikk med hensyn til massesenteret og ω vinkelhastigheten. Det kan demonstreres at kinetisk energi er:
K = ½ mvCM2 + ½ iCM Ω2
Det observeres at den andre begrepet til høyre er rotasjonsanalogen til Venstre -betegnelsen. Der spiller treghetsøyeblikket samme rolle som massen, mens vinkelhastigheten har samme rolle som den lineære hastigheten.
Eksempler i hverdagen
Fysisk pendel
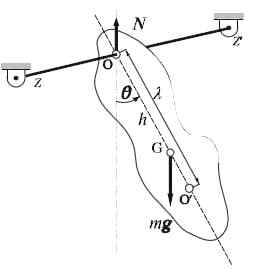 Fysisk pendel
Fysisk pendel Den fysiske pendelen eller ekte pendelen er veldig enkel å bygge: den består av et stivt fast stoff som en stang eller stang, som svinger fritt rundt en horisontal akse. Rotasjonsaksen krysser ikke massesenteret til objektet, og dette i prinsippet kan ha noen form.
Kan tjene deg: motstandstermometer: egenskaper, drift, brukDenne pendelen skiller seg fra den enkle pendelen, for i sistnevnte anses det at massen som komponerer den er punktlig.
Sykkelhjul
 Sykkelhjul
Sykkelhjul Et annet kjent stivt kroppseksempel er sykkelhjulet, hvis akse passerer gjennom massesenteret, som krysser midten av hjulet. Så lenge de ikke lener seg til siden eller svinger, gjelder ligningene til den beskrevne dynamikken for å beskrive bevegelsen din.
En bowlingball
 Et godt eksempel på en stiv kropp er bowlingballen
Et godt eksempel på en stiv kropp er bowlingballen Den stive solide modellen tilpasser seg veldig bra for å beskrive bevegelsen av bowlingballen på banen eller når den ruller uten å skyve ned returrampen.
Yoyoen
 Yoyo er et populært leketøy som kan modelleres som en stiv kropp
Yoyo er et populært leketøy som kan modelleres som en stiv kropp Dette populære leketøyet er laget med en tre- eller plastsylinder og et tau overveldet i en spalte som omgir det.
Sylinderen kan modelleres som en stiv kropp der spenningen i strengen gir dreiemomentet for rotasjonen, mens vekten (påført massesenteret) og spenningen er ansvarlig for den vertikale akselerasjonen av massesenteret.
Referanser
- Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
- Giancoli, d. 2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
- Katz, d. 2013. Fysikk for forskere og ingeniører. Grunnlag og tilkoblinger. Cengage Learning.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. Pearson.
- Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.