Hva er plasseringen av hele og desimaltall?

De Plassering av hele og desimaltall Det er avgrenset av et komma, også kalt koma -desimal. Hele delen av et reelt tall er skrevet til venstre for komma, mens desimaldelen av tallet er skrevet til høyre.

Den universelle notasjonen om å skrive en hel del og desimaldelen skiller disse delene med komma, men det er steder hvor de bruker et punkt.

I det forrige bildet kan vi se at hele delen av et av de virkelige tallene er 21, mens desimaldelen er 735.

Plassering av hele delen og desimaldelen

Det ble allerede beskrevet at når et reelt tall er skrevet, er notasjonen som ble brukt for å skille hele sin del fra desimaldelen, et komma, som vil vite hvordan man finner hver del av det gitte nummeret.

Nå, akkurat som hele delen er delt inn i enheter, titalls, hundrevis og mer, er desimaldelen også delt inn i følgende deler:

-Tiendedeler: Det er det første nummeret til høyre for komma.

-Hundredeler: Det er det andre nummeret til høyre for komma.

-Tusenvis: Det er det tredje tallet til venstre for komma.

Derfor leses bildenummeret i begynnelsen som "21 med 735 tusendeler".

Et kjent faktum er at når et tall er hele.

Når det gjelder desimaldelen, skjer det noe lignende, med forskjellen om at nuller må legges til høyre slik at de ikke påvirker verdien, for eksempel tallene 21 735 og 21 73500 er faktisk det samme tallet.

Med det som ble sagt ovenfor, kan det konkluderes med at desimaldelen av ethvert heltall er null.

Den virkelige linjen

På den annen side, når den virkelige linjen er trukket, begynner den med å tegne en horisontal linje, deretter i sentrum er nullverdien plassert og til høyre for nullen en verdi som verdien på 1 er tildelt er merket.

Avstanden mellom to påfølgende heltall er alltid 1. Derfor, hvis vi plasserer dem på den virkelige linjen, får vi en graf som den neste.

Ved første øyekast kan du tro at mellom to heltall er det ingen reelle tall, men sannheten er at det er uendelige reelle tall, som er delt inn i rasjonelle og irrasjonelle tall.

Rasjonelle og irrasjonelle tall, plassert mellom hele tall n og n+1, har en hel del av n, mens desimaldelen deres varierer langs hele linjen.

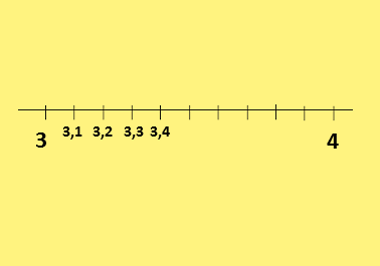
For eksempel, hvis du vil finne nummeret 3.4 på den virkelige linjen, er det først plassert der 3 og 4 er. Nå er dette linjesegmentet delt inn i 10 deler av samme lengde. Hvert segment vil ha en lengde på 1/10 = 0,1.

Som du vil finne tallet 3.4, blir 4 segmenter av lengde 0.1 talt til høyre for nummer 3.

Hele og desimaltall brukes nesten overalt, fra målene til et objekt til prisen på et produkt i et lager.