Hva er delingene av 30? (Forklaring)
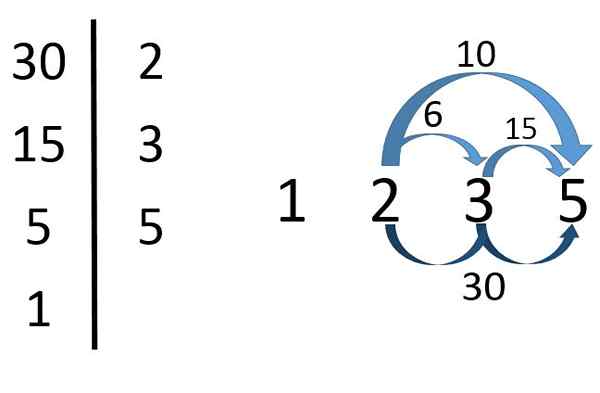
- 1952
- 331
- Theodor Anders Hopland
Divisorene på 30 er 1, 2, 3, 5, 6, 10, 15 og 30. Vi forklarer hvorfor og hvordan du kan beregne det selv.
Raskt, kan bli kjent Hva er delingene av 30, så vel som alle andre tall (forskjellig fra null), men den grunnleggende ideen er å lære hvordan deling av et antall beregnes på en generell måte.
Det bør utvises forsiktighet når du snakker om delere, fordi det raskt kan fastslås at alle delere av 30 er 1, 2, 5, 6, 10, 15 og 30, men hva med negativene til disse tallene? Er delinger eller ikke?
For å svare på det forrige spørsmålet, er det nødvendig å forstå et veldig viktig begrep i matematikkens verden: Divisjonsalgoritmen.
Divisjonsalgoritme
Divisjonsalgoritmen (eller Euclidian Division) sier følgende: Gitt to heltall "N" og "B", er "B" forskjellig fra null (B ≠ 0), er det unike "Q" og "R", slik at n = bq+r, der 0 ≤ r < |b|.
Antallet "n" kalles utbytte, "B" kalles divisor, "Q" kalles kvotient og "r" kalles resten eller avfall. Når resten "R" er lik 0, sies det at "B" deler "N", og dette er betegnet med "B | n".
Divisjonsalgoritmen er ikke begrenset til positive verdier. Derfor kan et negativt tall være divisor fra et annet tall.
Hvorfor 7.5 ikke er en divisor på 30?
Ved hjelp av divisjonsalgoritmen kan det sees at 30 = 7,5 × 4+0. Resten er lik null, men det kan ikke sies at 7,5 deler 30 fordi når de snakker om delere er det bare hele tall som blir snakket om.
Kan tjene deg: Eksponentiell funksjon: egenskaper, eksempler, øvelserDivisorer på 30
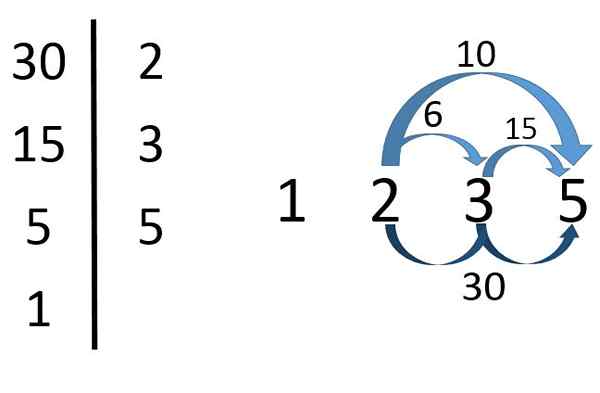 Divisorer på 30
Divisorer på 30 Som det fremgår av bildet, må du finne delene av 30 først.
Deretter 30 = 2x3x5. Herfra er det konkludert med at 2, 3 og 5 De er deling av 30. Men det er også produktene fra disse primfaktorene.
Slik at 2 × 3 =6, 2 × 5 =10, 3 × 5 =femten og 2x3x5 =30 De er deling av 30. Han 1 Det er også en divisor på 30 (selv om det i virkeligheten er en divisor av et hvilket som helst tall).
Det kan konkluderes med at 1, 2, 3, 5, 6, 10, 15 og 30 er deling av 30 (Alle oppfyller divisjonsalgoritmen), men vi må huske at deres negativer også er deling.
Derfor er alle delingene av 30: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 og 30.
Det som er lært ovenfor, kan brukes med ethvert hele antall.
For eksempel, hvis du vil beregne delingene av 92, fortsett som før. Det brytes sammen som et produkt av primtall.
92 er delt med 2 og oppnådd 46; Nå er 46 delt med 2 igjen og får 23.
Dette siste resultatet er et primtall, så det vil ikke ha flere delinger i tillegg til 1 og de samme 23.
Vi kan deretter skrive 92 = 2x2x23. Fortsetter som før, er det konkludert med at 1,2,46 og 92 er 92 delinger.
Til slutt er negativene av disse tallene til forrige liste inkludert, som er listen over alle delingene av 92 er -92, -46, -4, -2, -1, 1, 2, 4, 46, 46, 92.
- « Aktiviteter for barn med læringsproblemer
- Hvor mange hundrelapper som passer i en tiende? (Eksempler) »

