Hvor mange løsninger har en kvadratisk ligning?

En kvadratisk ligning eller andre grads ligning kan ha null, en eller to virkelige løsninger, avhengig av koeffisientene som vises i nevnte ligning. Hvis du jobber med komplekse tall, kan du si at hver kvadratiske ligning har to løsninger.

For å starte en kvadratisk ligning er det en ligning av AX²+BX+C = 0 Form, hvor A, B og C er reelle tall og X er en variabel.

Det sies at x1 er en løsning av den forrige kvadratiske ligningen hvis når du erstatter x med x1, er ligningen tilfredsstilt, det vil si hvis a (x1) ²+b (x1)+c = 0.

Hvis du for eksempel har ligningen x²-4x+4 = 0, er x1 = 2 løsningen, siden (2) ² (2) +4 = 4-8+4 = 0.

Tvert imot, hvis x2 = 0 blir erstattet, oppnås det (0) ²-4 (0) +4 = 4 og som 4 ≠ 0 da er ikke en løsning av den kvadratiske ligningen.

Løsninger av en kvadratisk ligning

Antall løsninger av en kvadratisk ligning kan skilles i to tilfeller som er:

1.- I reelle tall

Når du jobber med reelle tall, kan kvadratiske ligninger ha:

-Null løsninger: det vil si at det ikke er noe reelt tall som tilfredsstiller den kvadratiske ligningen. For eksempel er ligningen gitt x²+1 = 0, det er ikke noe reelt tall slik som tilfredsstiller nevnte ligning, siden begge x² er større enn eller lik null og 1 er større streng enn null, slik at summen vil være større vil være Streng enn null.

-En gjentatt løsning: Det er en reell verdi som tilfredsstiller den kvadratiske ligningen. For eksempel er den eneste løsningen av ligning x²-4x+4 = 0 x1 = 2.

-To forskjellige løsninger: Det er to verdier som tilfredsstiller den kvadratiske ligningen. For eksempel har x²+x -2 = 0 to forskjellige løsninger som er x1 = 1 og x2 = -2.

2.- I komplekse tall

Når du jobber med komplekse tall, har kvadratiske ligninger alltid to løsninger, som er Z1 og Z2 der Z2 er konjugatet til Z1. I tillegg kan de klassifiseres som:

-Komplekser: Løsningene er av formen z = p ± qi, der p og q er reelle tall. Denne saken tilsvarer det første tilfellet av forrige liste.

-Rene komplekser: Det er når den virkelige delen av løsningen er lik null, det vil si at løsningen har formen z = ± qi, der Q er et reelt tall. Denne saken tilsvarer det første tilfellet av forrige liste.

-Komplekser med imaginær del lik null: Det er når den komplekse delen av løsningen er lik null, det vil si at løsningen er et reelt tall. Denne saken tilsvarer de to siste tilfellene av forrige liste.

Hvordan beregnes løsningene på en kvadratisk ligning?

For å beregne løsningene av en kvadratisk ligning brukes en formel kjent som "oppløsningen", som sier at løsningene til en AX²+BX+C = 0 -ligning er gitt ved uttrykk for følgende bilde:

Mengden som vises i kvadratroten kalles diskriminerende av den kvadratiske ligningen og er betegnet med bokstaven "d".

Den kvadratiske ligningen vil ha:

-To virkelige løsninger ja, og bare ja, d> 0.

-En gjentatt ekte løsning hvis, og bare hvis, d = 0.

-Null virkelige løsninger (eller to komplekse løsninger) Ja, og bare ja, D<0.

Eksempler

-Løsningene av ligningen x²+x-2 = 0 er gitt av:

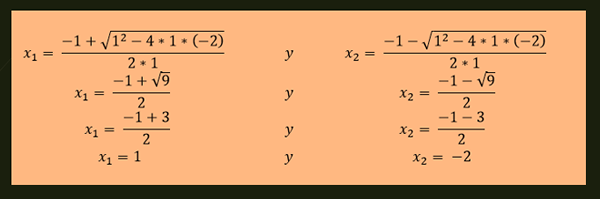
-Ligningen x²-4x+4 = 0 har en gjentatt løsning som er gitt av:

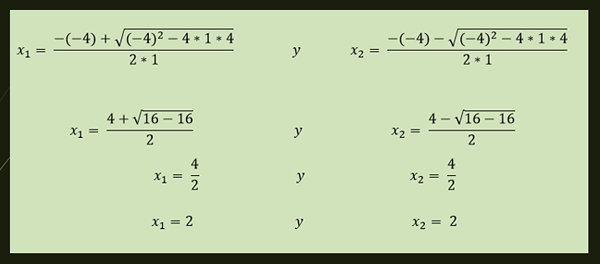
-Løsningene av ligningen x²+1 = 0 er gitt av:

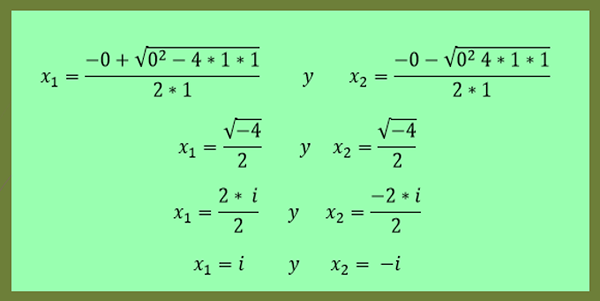
Som det kan sees i dette siste eksemplet, er X2 konjugatet til X1.